

Next: Observables and single particle
Up: hfbrad23w
Previous: Pairing correlations and divergence
The effective Skyrme force
For a general overview of the foundations and properties of the
Skyrme force we refer the reader to the review article
[20] and references therein.
The Skyrme force is an effective interaction
depending on a limited number of parameters,
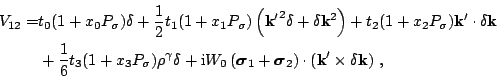 |
(43) |
where 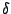 is a short notation for
is a short notation for
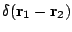 ,
,
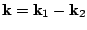 acting on the right and
acting on the right and
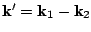 acting on the left.
acting on the left.
The parameters of the Skyrme forces were fitted in the literature
to reproduce various bulk nuclear properties as well as selected
properties of some nuclei (usually
doubly magic nuclei). Simplifications have often been
made in the expression of the functional (19), like
treatment of the Coulomb
exchange term with the Slater approximation and/or omission
of the two-body center of mass contribution or of the ``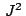 ''
terms.
The latter corresponds to the fourth line in Eq. (19)
and to the two first terms in the spin-orbit mean field, Eq. (29).
It is important to keep in mind that one should use each parametrization
of the functional within the same simplifications with which it has
been adjusted to data.
''
terms.
The latter corresponds to the fourth line in Eq. (19)
and to the two first terms in the spin-orbit mean field, Eq. (29).
It is important to keep in mind that one should use each parametrization
of the functional within the same simplifications with which it has
been adjusted to data.
For all forces implemented in HFBRAD, the
force in the particle-particle channel is chosen to be
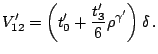 |
(44) |
Table 1 gives the different sets of parameters
for the force in the particle-hole channel, while table 2
gives the parameters in the particle-particle channel. It is
important to keep in mind that these latter parameters have been
adjusted along with a given cut-off and cut-off diffuseness, which
are two additional parameters of the force.
Table 1:
Parameters in the particle-hole channel for
the different versions of the Skyrme forces implemented
in the code HFBRAD. The last line indicates if the
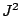 terms are included in the Skyrme functional
when the force is used.
terms are included in the Skyrme functional
when the force is used.
| |
SIII [4] |
SkM* [21] |
. | SLy4 [22] |
. | SLy5 [22] |
. | SkP [5] |
. | |
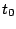 |
 1128 1128 |
. | 75 |
 2645 2645 |
. | 0 |
 2488 2488 |
. | 913 |
 2488 2488 |
. | 345 |
 2931 2931 |
. | 6960 |
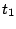 |
395 |
. | 0 |
410 |
. | 0 |
486 |
. | 818 |
484 |
. | 230 |
320 |
. | 6182 |
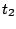 |
 95 95 |
. | 0 |
 135 135 |
. | 0 |
 546 546 |
. | 395 |
 556 556 |
. | 690 |
 337 337 |
. | 4091 |
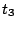 |
14000 |
. | 0 |
15595 |
. | 0 |
13777 |
. | 0 |
13757 |
. | 0 |
18708 |
. | 96 |
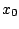 |
0 |
. | 45 |
0 |
. | 09 |
0 |
. | 834 |
0 |
. | 776 |
0 |
. | 2921515 |
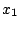 |
0 |
. | 0 |
0 |
. | 0 |
 0 0 |
. | 344 |
 0 0 |
. | 317 |
0 |
. | 6531765 |
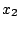 |
0 |
. | 0 |
0 |
. | 0 |
 1 1 |
. | 000 |
 1 1 |
. | 000 |
 0 0 |
. | 5373230 |
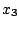 |
1 |
. | 0 |
0 |
. | 0 |
1 |
. | 354 |
1 |
. | 263 |
0 |
. | 1810269 |
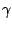 |
1 |
. | 0 |
1 |
. | 6 |
1 |
. | 6 |
1 |
. | 6 |
1 |
. | 6 |
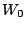 |
130 |
. | 0 |
120 |
. | 0 |
123 |
. | 0 |
125 |
. | 00 |
100 |
. | 000 |
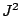 |
No |
No |
. | No |
. | Yes |
. | Yes |
. | |
|
Three kinds of pairing forces have been adjusted: (i) the volume
pairing (the pairing field follows the shape of the density), below
denoted by ``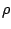 '', (ii) the surface pairing (the pairing field is
peaked at the surface and follows roughly the variations of the
density), below denoted by `'
'', (ii) the surface pairing (the pairing field is
peaked at the surface and follows roughly the variations of the
density), below denoted by `'
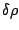 '', and (iii) the mixed
pairing (a compromise between the two first two), below denoted by
``
'', and (iii) the mixed
pairing (a compromise between the two first two), below denoted by
``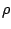 +
+
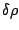 ''. All pairing parameters have been adjusted in
order to give a mean neutron gap of 1.245 MeV in
''. All pairing parameters have been adjusted in
order to give a mean neutron gap of 1.245 MeV in 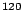 Sn.
Sn.
Table 2:
Parameters in the particle-particle channel for
the different versions of the Skyrme forces implemented
in the code HFBRAD. The three first columns corresponds
to the use of a cut-off
at 60 MeV with a Fermi shape and a diffuseness of
1 MeV, the three columns on the right corresponds to
the regularization procedure of the pairing field
described in Sec. 2.7.
| |
cut-off |
regularization |
| |
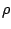 |
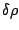 |
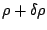 |
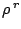 |
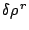 |
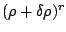 |
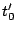 (SIII) (SIII) |
 159.6 159.6 |
 483.2 483.2 |
 248.5 248.5 |
 197.6 197.6 |
 807.0 807.0 |
 316.9 316.9 |
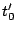 (SkM*) (SkM*) |
 148.6 148.6 |
 452.6 452.6 |
 233.9 233.9 |
 184.7 184.7 |
 798.4 798.4 |
 300.7 300.7 |
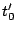 (SLy4) (SLy4) |
 186.5 186.5 |
 509.6 509.6 |
 283.3 283.3 |
 233.0 233.0 |
 914.2 914.2 |
 370.2 370.2 |
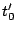 (SLy5) (SLy5) |
 179.9 179.9 |
 504.9 504.9 |
 275.8 275.8 |
 222.7 222.7 |
 901.9 901.9 |
 356.6 356.6 |
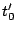 (SkP) (SkP) |
 131.6 131.6 |
 429.5 429.5 |
 213.1 213.1 |
 196.6 196.6 |
 1023.0 1023.0 |
 326.5 326.5 |
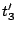 |
0 |
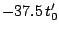 |
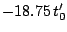 |
0 |
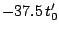 |
 |
 |
1 |
1 |
1 |
1 |
1 |
1 |
|


Next: Observables and single particle
Up: hfbrad23w
Previous: Pairing correlations and divergence
Jacek Dobaczewski
2005-01-23
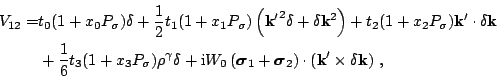
![]() ''
terms.
The latter corresponds to the fourth line in Eq. (19)
and to the two first terms in the spin-orbit mean field, Eq. (29).
It is important to keep in mind that one should use each parametrization
of the functional within the same simplifications with which it has
been adjusted to data.
''
terms.
The latter corresponds to the fourth line in Eq. (19)
and to the two first terms in the spin-orbit mean field, Eq. (29).
It is important to keep in mind that one should use each parametrization
of the functional within the same simplifications with which it has
been adjusted to data.
![]() '', (ii) the surface pairing (the pairing field is
peaked at the surface and follows roughly the variations of the
density), below denoted by `'
'', (ii) the surface pairing (the pairing field is
peaked at the surface and follows roughly the variations of the
density), below denoted by `'
![]() '', and (iii) the mixed
pairing (a compromise between the two first two), below denoted by
``
'', and (iii) the mixed
pairing (a compromise between the two first two), below denoted by
``![]() +
+
![]() ''. All pairing parameters have been adjusted in
order to give a mean neutron gap of 1.245 MeV in
''. All pairing parameters have been adjusted in
order to give a mean neutron gap of 1.245 MeV in ![]() Sn.
Sn.