


Next: Tensor interaction and the
Up: GLOBAL NUCLEAR STRUCTURE ASPECTS
Previous: Introduction
Figure 1:
The
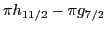 splitting in
splitting in
 Sn isotopes versus
Sn isotopes versus  . Black triangles label
empirical data taken from Ref. [18]. Open and gray
symbols represent the SHF results obtained by using the SLy4 (left)
SkO (middle), and SLy5 (right) parameterizations, respectively.
Different symbols labeling theoretical results
follow the SHF minima corresponding to configurations differing in
the
. Black triangles label
empirical data taken from Ref. [18]. Open and gray
symbols represent the SHF results obtained by using the SLy4 (left)
SkO (middle), and SLy5 (right) parameterizations, respectively.
Different symbols labeling theoretical results
follow the SHF minima corresponding to configurations differing in
the 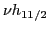 occupancies as indicated in the legend.
occupancies as indicated in the legend.
|
|
The s.p. levels constitute one of the main building blocks of the MF method. In spite
of that, the Skyrme HF (SHF) method that uses forces fitted to
bulk nuclear properties performs rather poorly with regard to
the s.p. SO splittings[28,30]. This is visualized in
Fig. 1, showing the
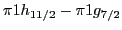 splittings,
splittings,
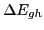 , in antimony, calculated by using the
SLy4[35], SkO[36], and SLy5[35]
parameterizations. The SLy4 force strongly overestimates the
absolute value of
, in antimony, calculated by using the
SLy4[35], SkO[36], and SLy5[35]
parameterizations. The SLy4 force strongly overestimates the
absolute value of 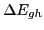 and fails to reproduce the
slope of the
and fails to reproduce the
slope of the
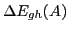 curve. The non-standard isovector SO in the
SkO force helps by reducing, on average, the splitting to the empirical level, but
does not change the slope of the
curve. The non-standard isovector SO in the
SkO force helps by reducing, on average, the splitting to the empirical level, but
does not change the slope of the
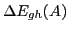 curve. Finally, in SLy5,
the inclusion of
tensor terms changes the slope, but shifts the theoretical curves in a wrong
direction. The latter observation suggests that the fit to masses leads to
values of tensor
coupling constants that are at variance with those deduced from the s.p. level analysis, see Refs.[37,28]. However, one should point out
that the
curve. Finally, in SLy5,
the inclusion of
tensor terms changes the slope, but shifts the theoretical curves in a wrong
direction. The latter observation suggests that the fit to masses leads to
values of tensor
coupling constants that are at variance with those deduced from the s.p. level analysis, see Refs.[37,28]. However, one should point out
that the
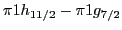 splittings depend upon many factors including, apart from the SO and
tensor fields, the effective mass, centroid energies of the
splittings depend upon many factors including, apart from the SO and
tensor fields, the effective mass, centroid energies of the 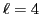 and
and
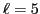 sub-shells, and strong polarization effects. Hence, conclusions
concerning the SO and tensor coupling constants that are deduced solely from
these data should be considered to be tentative.
sub-shells, and strong polarization effects. Hence, conclusions
concerning the SO and tensor coupling constants that are deduced solely from
these data should be considered to be tentative.
Figure 2:
The neutron (top) and proton
(bottom)
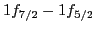 SO splittings in
SO splittings in
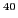 Ca,
Ca, 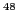 Ca, and
Ca, and 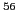 Ni. Black symbols show the
mean empirical values taken from Refs.[38,39] and
open dots denote the SkO results. Open diamonds represent the
results obtained by using the SkO
Ni. Black symbols show the
mean empirical values taken from Refs.[38,39] and
open dots denote the SkO results. Open diamonds represent the
results obtained by using the SkO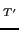 functional
of Ref.[40], which includes strong attractive tensor
terms and a reduced SO strength.
functional
of Ref.[40], which includes strong attractive tensor
terms and a reduced SO strength.
|
|
It is well known, see Refs.[41,42], that
the tensor interaction strongly modifies the SO one-body potential.
In the spherical-symmetry limit, the isoscalar (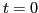 ) and isovector (
) and isovector (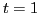 )
SO one-body potentials read:
)
SO one-body potentials read:
where 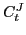 and
and
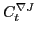 are the tensorial and spin-orbit
coupling constants, see for example Ref.[28]. The tensor field
depends upon the radial component of the spin-orbit vector density
are the tensorial and spin-orbit
coupling constants, see for example Ref.[28]. The tensor field
depends upon the radial component of the spin-orbit vector density
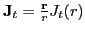 that measures the
spin-asymmetry of the nucleus and can rapidly vary with particle numbers. On the contrary,
the second term in Eq. (1), which is due to the conventional two-body
spin-orbit interaction, depends on the radial
derivative of the particle density
that measures the
spin-asymmetry of the nucleus and can rapidly vary with particle numbers. On the contrary,
the second term in Eq. (1), which is due to the conventional two-body
spin-orbit interaction, depends on the radial
derivative of the particle density 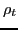 , which varies relatively slowly
with particle numbers. Such a contrasting behavior of the two major constituents of
the SO potential can be actually used to fit the
coupling constants to data[28]. The idea is visualized in
Fig. 2, which shows the
, which varies relatively slowly
with particle numbers. Such a contrasting behavior of the two major constituents of
the SO potential can be actually used to fit the
coupling constants to data[28]. The idea is visualized in
Fig. 2, which shows the
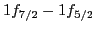 SO splittings in
SO splittings in 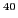 Ca,
Ca,
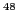 Ca, and
Ca, and 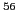 Ni. These splittings form a very distinct pattern
that cannot be reproduced based solely on the conventional SO potential.
Indeed, the
Ni. These splittings form a very distinct pattern
that cannot be reproduced based solely on the conventional SO potential.
Indeed, the
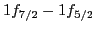 SO splittings in
SO splittings in 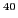 Ca,
Ca,
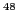 Ca, and
Ca, and 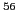 Ni are fairly constant when calculated using,
for example the SkO force, see curve marked by open dots in
Fig. 2. It reflects the fact that
the neutron and proton radial form-factors
Ni are fairly constant when calculated using,
for example the SkO force, see curve marked by open dots in
Fig. 2. It reflects the fact that
the neutron and proton radial form-factors
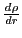 almost do not
change when going from
almost do not
change when going from 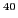 Ca through
Ca through 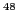 Ca to
Ca to 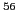 Ni.
At the same time the neutron and proton SO vector
densities
Ni.
At the same time the neutron and proton SO vector
densities 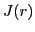 change rapidly when
going from the isoscalar spin-saturated
change rapidly when
going from the isoscalar spin-saturated 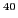 Ca to the isoscalar
spin-unsaturated nucleus
Ca to the isoscalar
spin-unsaturated nucleus 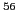 Ni, and, finally, to the isovector spin-unsaturated nucleus
Ni, and, finally, to the isovector spin-unsaturated nucleus 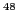 Ca.
This allows for a simple and intuitive three-step fitting procedure[28] of
the
Ca.
This allows for a simple and intuitive three-step fitting procedure[28] of
the
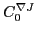 in
in 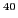 Ca,
Ca, 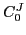 in
in 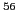 Ni, and
Ni, and
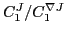 ratio in
ratio in 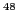 Ca.
This procedure leads to (i) a significant reduction in the isoscalar
SO strength and (ii) strong attractive tensor coupling constants.
It systematically
improves such s.p. properties as the SO splittings
and magic-gap energies[28], but leads to deteriorated nuclear binding energies.
Ca.
This procedure leads to (i) a significant reduction in the isoscalar
SO strength and (ii) strong attractive tensor coupling constants.
It systematically
improves such s.p. properties as the SO splittings
and magic-gap energies[28], but leads to deteriorated nuclear binding energies.



Next: Tensor interaction and the
Up: GLOBAL NUCLEAR STRUCTURE ASPECTS
Previous: Introduction
Jacek Dobaczewski
2009-04-13
![\includegraphics[width=11.5cm,clip]{K08-f1.eps}](img12.png)
![\includegraphics[width=11.5cm,clip]{K08-f1.eps}](img12.png)
![]() splittings,
splittings,
![]() , in antimony, calculated by using the
SLy4[35], SkO[36], and SLy5[35]
parameterizations. The SLy4 force strongly overestimates the
absolute value of
, in antimony, calculated by using the
SLy4[35], SkO[36], and SLy5[35]
parameterizations. The SLy4 force strongly overestimates the
absolute value of ![]() and fails to reproduce the
slope of the
and fails to reproduce the
slope of the
![]() curve. The non-standard isovector SO in the
SkO force helps by reducing, on average, the splitting to the empirical level, but
does not change the slope of the
curve. The non-standard isovector SO in the
SkO force helps by reducing, on average, the splitting to the empirical level, but
does not change the slope of the
![]() curve. Finally, in SLy5,
the inclusion of
tensor terms changes the slope, but shifts the theoretical curves in a wrong
direction. The latter observation suggests that the fit to masses leads to
values of tensor
coupling constants that are at variance with those deduced from the s.p. level analysis, see Refs.[37,28]. However, one should point out
that the
curve. Finally, in SLy5,
the inclusion of
tensor terms changes the slope, but shifts the theoretical curves in a wrong
direction. The latter observation suggests that the fit to masses leads to
values of tensor
coupling constants that are at variance with those deduced from the s.p. level analysis, see Refs.[37,28]. However, one should point out
that the
![]() splittings depend upon many factors including, apart from the SO and
tensor fields, the effective mass, centroid energies of the
splittings depend upon many factors including, apart from the SO and
tensor fields, the effective mass, centroid energies of the ![]() and
and
![]() sub-shells, and strong polarization effects. Hence, conclusions
concerning the SO and tensor coupling constants that are deduced solely from
these data should be considered to be tentative.
sub-shells, and strong polarization effects. Hence, conclusions
concerning the SO and tensor coupling constants that are deduced solely from
these data should be considered to be tentative.
![\includegraphics[width=12cm,clip]{K08-f2.eps}](img20.png)
![]() ) and isovector (
) and isovector (![]() )
SO one-body potentials read:
)
SO one-body potentials read: