Mini-PET

W tym przykładzie zaprezentowane będą różne przydatne techniki używane podczas eksploracyjnej analizy danych. Przykładowe dane pochodzą z Pracowni Fizycznej dla zaawansowanych z ćwiczenia mini-PET.

Pozytronowa tomografia emisyjna (PET) to technika obrazowania medycznego wykorzystującego promieniowanie jądrowe. Do organizmu wprowadzany jest izotop promieniotwórczy ulegający rozpadowi beta plus. Podczas tej przemiany emitowany jest pozyton (e+e^+), który w niewielkiej odległości od miejsca emisji ulega anihilacji z elektronem z materii. Proces anihilacji prowadzi do emisji dwóch kwantów gamma o energii równej masie elektronu (511 keV), które są emitowane w przeciwnych kierunkach. Jeżeli w otaczających pacjenta detektorach są będą one jednocześnie zarejestrowane, to będziemy wiedzieli, że na prostej łączącej detektory znajdowało się źródło promieniowania. Po zarejestrowaniu wielu tego typu zdarzeń, z przecięcia się linii możemy bardzo precyzyjnie zlokalizować przestrzennie źródło.

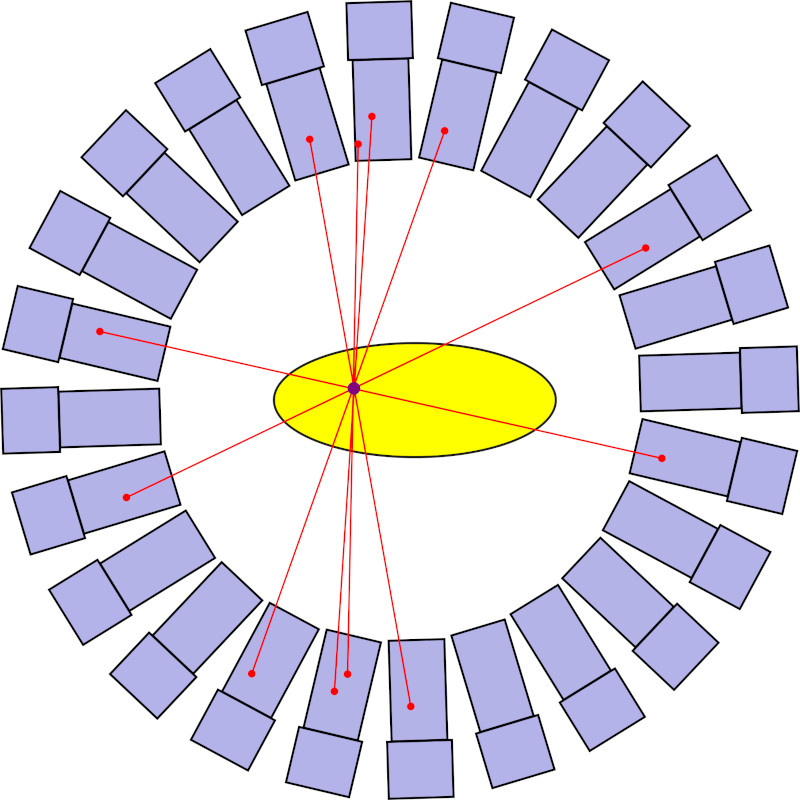
pet.jpg

Na pracowni mini-PET używa tylko jednej pary detektorów, ale istnieje możliwość przesuwania próbki. Aby znaleźć położenie źródła w fantomie, z dokładnością poniżej 1 mm, zwykle potrzeba około 20-30 pomiarów.

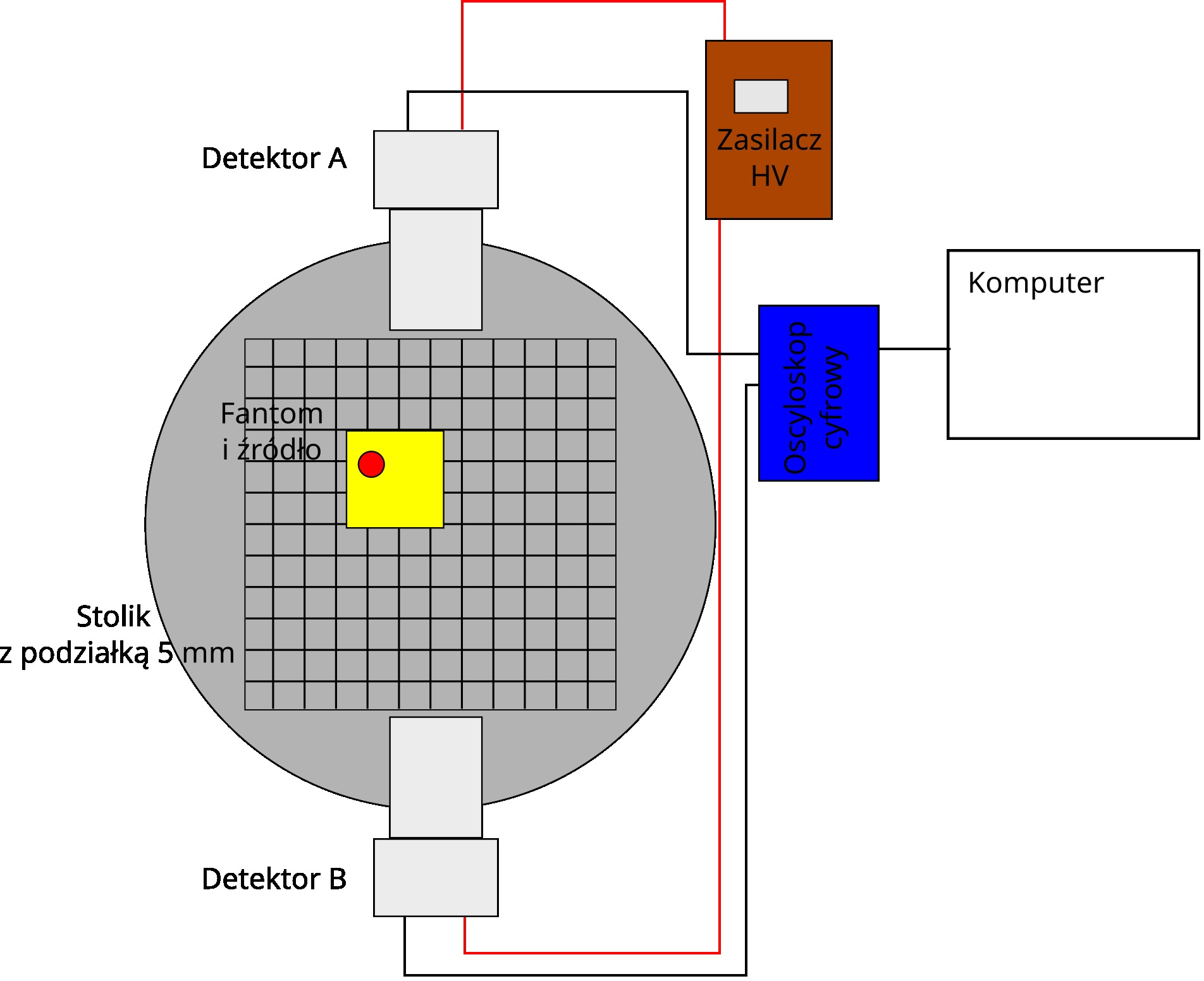
minipet.jpg

Przy tej ilości danych wciąż możliwe jest ich ręczne analizowanie, aczkolwiek może to być nużące i lepiej jest analizować je bardziej automatycznie. Tym bardziej, że jednym z głównych zagadnień analizy jest wybór poprawnych zdarzeń i analiza skuteczności różnych kryteriów wyboru. Jest to dobra ilustracja zagadnień jakie możemy napotkać przy analizie danych i spróbujemy poddać analizie przykładowy plik z pomiarów.

Plik jest w postaci tekstowej i ma postać:

# Start at 2020-03-12 18:08:26.630562
# EA  EB  tA  tB
# 
34.336 1.711 88.993 10.038
43.069 0.252 101.128 30.000
87.309 2.216 112.389 11.143
43.530 0.000 103.681 0.000
...
34.321 0.000 89.943 9.586
55.688 3.609 107.365 341.424
# Stop at 2020-03-12 18:13:26.785269
# Total running time: 300.155 s
# Total events: 20016

Jest tu nagłówek i stopka (ogólnie komentarze) oznaczone symbolami '#'. Właściwe dane są w 4 kolumnach, każdy wiersz odpowiada jednemu zdarzeniu zarejestrowanemu przez układ detektorów: energia w detektorze A i detektorze B (bezwymiarowe wielkości w kanałach ADC), względny czas detekcji w detektorze A i B (w ns).

Zaczniemy od wczytania danych do struktury DataFrame. Plik nie jest w formacie CSV, ale jeżeli podpowiemy parserowi jaki znak oznacza komentarz, a jaki oddziela kolumny, to możemy go wczytać automatycznie. Ponieważ nazwy kolumn są ukryte w linii komentarza, nadamy je ręcznie (teoretycznie moglibyśmy wczytać tę linię, usunąć znak komentarza, podzielić na ciągi i wygenerować nazwy automatycznie, ale w tym przypadku byłoby to więcej pracy niż pożytku).

using DataFrames
using CSV

df = DataFrame(CSV.File("minipet.txt", comment="#", header=false, delim=" ", ignorerepeated=true))
rename!(df, ["EA", "EB", "tA", "tB"])

Aby zorientować się co w gruncie rzeczy zawierają dane narysujemy widma energii (histogramy) dla obu detektorów

using StatsBase
using GRUtils

hA = fit(Histogram, df.EA, nbins=1000)
plot(hA.edges[1][1:end-1], hA.weights, "g-")
hold(true)

hB = fit(Histogram, df.EB, nbins=1000)
plot(hB.edges[1][1:end-1], hB.weights, "r-")

legend("A", "B")
hold(false)
display(gcf())

Wykres jest mało czytelny, ponieważ detektor B zawiera mnóstwo zdarzeń o małych wartościach. Jest to związane z tym, że sygnał wyzwalający pochodzi z detektora A i jeżeli jest tam sygnał powyżej pewnego progu to rejestrowany jest także sygnał B, gdzie często jest tylko szum. Ponieważ nie są to interesujące informacje, ręcznie podamy zakres histogramu.

hA = fit(Histogram, df.EA, 20:2:500)
plot(hA.edges[1][1:end-1], hA.weights, "g-")
hold(true)
hB = fit(Histogram, df.EB, 20:2:500)
plot(hB.edges[1][1:end-1], hB.weights, "r-")
legend("A", "B")
hold(false)
display(gcf())

Linia pojawiająca się w detektorze A pomiędzy 100 i 160 kanałem to właśnie kwant gamma 511 keV. W detektorze B jest ona pomiędzy 180 i 240 kanałem. W detektorze A widać także linię 1274 keV (kanały 300 - 380). W detektorze B jest ona poza zakresem dynamicznym.

Kalibrację detektora powinniśmy przeprowadzić w zasadzie w oparciu o źródła kalibracyjne zanim przystąpimy do właściwych pomiarów, ale na potrzeby ilustracji wykorzystamy te same dane do kalibracji. Ponieważ mamy tylko jedną linię w detektorze B, założymy, że kanał 0 odpowiada energii 0, a drugim punktem będzie linia 511 keV.

Położenie linii znajdziemy poprzez dopasowanie funkcji Gaussa z liniowym tłem do widma.

N(x)=A2πσ2exp⁡(−(x−μ)22σ2)+a0+a1x N(x) = \frac{A}{\sqrt{2\pi \sigma^2}} \exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right) + a_0 + a_1x

Funkcja gauss(x, p) oprócz zmiennej x pobiera listę parametrów:

  • p[1] = μ\mu

  • p[2] = A

  • p[3] = σ\sigma

  • p[4] = a0a_0

  • p[5] = a1a_1

Interesujące nas kanały będą znajdowały się w indeksach 46-71 i 141-181 dla detektora A (zaczęliśmy od 20 i szliśmy co 2) , oraz 81-111 dla detektora B. 

println(hA.edges[1][46:71], " ", hA.edges[1][141:181], " ", hB.edges[1][81:111])

Funkcja curve_fit z bibilioteki LsqFit dopasowuje funkcję do danych. Parametry to

curve_fit(model, xdata, ydata, p0)

gdzie model to funkcja pobierająca x i parametry, a p0 to początkowe parametry (powinniśmy podać sensowne przybliżenie, aby minimalizacja zbiegła do właściwego minimum).

using LsqFit

@. gauss(x, p) = p[2] / sqrt(2 * pi * p[3]^2) * exp(-(x - p[1])^2 / (2 * p[3]^2)) + p[4] + p[5] * x

fitA1 = curve_fit(gauss, hA.edges[1][46:71], hA.weights[46:71], [140.0, 1000.0, 10.0, 100.0, 0.0])

xf = 110:0.5:160
plot(hA.edges[1][46:71], hA.weights[46:71], "o")
hold(true)
plot(xf, gauss(xf, fitA1.param), "--")

Parametry dopasowania i niepewności możemy odczytać ze zwróconej informacji

using Printf

errs = standard_errors(fitA1)
names = ["μ", "A", "σ", "a₀", "a₁"]

for i in 1:length(fitA1.param)
    @printf("%s = %.3f ± %.3f \n", names[i], fitA1.param[i], errs[i])
end

Procedurę dopasowania powtórzymy dla pozostałych linii

fitA2 = curve_fit(gauss, hA.edges[1][141:181], hA.weights[141:181], [340.0, 1000.0, 10.0, 0.0, 0.0])
fitB1 = curve_fit(gauss, hB.edges[1][81:111], hB.weights[81:111], [210.0, 1000.0, 10.0, 0.0, 0.0])

subplot(1, 2, 1)
hold(false)
xf = 300:0.5:380
plot(hA.edges[1][141:181], hA.weights[141:181], "x")
hold(true)
plot(xf, gauss(xf, fitA2.param), "--")

subplot(1, 2, 2)
hold(false)
xf = 180:0.5:240
plot(hB.edges[1][81:111], hB.weights[81:111], "+")
hold(true)
plot(xf, gauss(xf, fitB1.param), "--")

Do położeń linii dopasujemy teraz liniową funkcję dla detektora A i B

lin(x, p) = p[1] .+ p[2] .* x

lines = [0.0, 511.0, 1274.5]

calA = curve_fit(lin, [0.0, fitA1.param[1], fitA2.param[1]], lines, [0.0, 1.0])
calB = curve_fit(lin, [0.0, fitB1.param[1]], lines[1:2], [0.0, 1.0])

@printf("EA = %.3f + %.3f x\n", calA.param[1], calA.param[2])
@printf("EB = %.3f + %.3f x\n", calB.param[1], calB.param[2])

Dodamy teraz nowe kolumny z wykalibrowanymi energiami rejestrowanymi w detektorach, a potem narysujemy histogramy.

lin(df.EA, calA.param)
transform!(df, [:EA] => (x -> lin(x, calA.param)) => :EAc)
transform!(df, [:EB] => (x -> lin(x, calB.param)) => :EBc)
Figure((800, 600), "pix")
hA = fit(Histogram, df.EAc, 20:5:1500)
plot(hA.edges[1][1:end-1], hA.weights, "g-")
hold(true)
hB = fit(Histogram, df.EBc, 20:5:1500)
plot(hB.edges[1][1:end-1], hB.weights, "r-")
legend("A", "B")
xlabel("E (keV)")

Sprawdźmy jak układają się zdarzenia na dwuwymiarowym wykresie EA vs. EB. Utniemy w histogramie najniższe kanały, aby wykres był czytelny.

hAB = fit(Histogram, (df.EAc, df.EBc), (20:10:1000, 20:10:1000))
Figure((800, 600), "pix")
heatmap(hAB.edges[1], hAB.edges[2], hAB.weights)
xlabel("EA (keV)")
ylabel("EB (keV)")

Widoczne jest jednoczesne występowanie zdarzeń o energii około 511 keV (rozrzut wynika z rozdzielczości energetycznej detektorów). Możemy wybrać te zdarzenia z listy stawiając odpowiednie warunki.

Figure((800, 600), "pix")
plot(hA.edges[1][1:end-1], hA.weights, "g-")
hold(true)
plot(hB.edges[1][1:end-1], hB.weights, "r-")
legend("A", "B")
xlabel("E (keV)")
xlim(400, 650)
xticks(10, 10)
sel1 = df[(490 .< df.EAc .< 550) .& (490 .< df.EBc .< 550), :]

Do tej pory sprawdziliśmy tylko widma energetyczne detektorów. Ale do dyspozycji mamy jeszcze względny czas rejestracji zdarzeń. Zobaczmy histogram różnicy w czasie pomiędzy detektorami.

Figure((800, 600), "pix")
tAB = fit(Histogram, df.tA - df.tB, nbins=1000)
plot(tAB.edges[1][1:end-1], tAB.weights, "-")

Zdarzenia o czasach około 100 ns są związane z rejestracją szumu w detektorze B. Ale jest pewna grupa zdarzeń o czasach około 0, która spełniałaby warunek jednoczesności rejestracji. Porównajmy jak wyglądają zdarzenia wybrane przez warunek energetyczny.

Figure((800, 600), "pix")
tAB = fit(Histogram, df.tA - df.tB, -50:0.5:50)
plot(tAB.edges[1][1:end-1], tAB.weights, "-")
hold(true)

tABsel1 = fit(Histogram, sel1.tA - sel1.tB, -50:0.5:50)
plot(tABsel1.edges[1][1:end-1], tABsel1.weights, "-")

Wszystkie wybrane w ten sposób zdarzenia mają rozkład czasowy bliski zera. Ale tego typu zdarzeń jest znacznie więcej! Może nasz warunek dobrego zdarzenia jest zbyt restrykcyjny? Być może niepotrzebnie redukujemy liczbę zdarzeń? Sprawdźmy jakie zdarzenia mają czas w okolicach zera.

sel2 = df[-5 .< df.tA - df.tB .< 5, :]
subplot(2, 2, 1)
hAsel2 = fit(Histogram, sel2.EAc, 0:10:1000)
plot(hAsel2.edges[1][1:end-1], hAsel2.weights, "-")
xlabel("\$E_A\$")

subplot(2, 2, 2)
hBsel2 = fit(Histogram, sel2.EBc, 0:10:1000)
plot(hBsel2.edges[1][1:end-1], hBsel2.weights, "-")
xlabel("\$E_B\$")


subplot(2, 2, (3, 4))

hABsel2 = fit(Histogram, (sel2.EAc, sel2.EBc), (0:10:1000, 0:10:1000))
heatmap(hABsel2.edges[1], hABsel2.edges[2], hABsel2.weights)
xlabel("E_B (keV)")
ylabel("E_A (keV)")

W obydwu detektorach mamy zdarzenia pełnej absorpcji, ale także rejestrację rozproszeń Comptona (kiedy kwant nie zostawia pełnej energii w detektorze). Nie musimy wyrzucać takich zdarzeń! Ale warunek oparty jedynie o czas jest nieco zbyt łagodny - nadal otrzymujemy zdarzenia o energii bliskiej 0 w detektorze B. Są to prawdopodobnie przypadkowe koincydencje z szumem.

Sprawdźmy tę koncepcję porównując widma dla zdarzeń o różnicy czasu pomiędzy 10 i 20 ns.

sel2b = df[10 .< df.tA - df.tB .< 20, :]
hAsel2b = fit(Histogram, sel2b.EAc, 0:10:1000)
plot(hAsel2b.edges[1][1:end-1], hAsel2b.weights, "-")
xlabel("\$E_A\$")

subplot(2, 2, 2)
hBsel2b = fit(Histogram, sel2b.EBc, 0:10:1000)
plot(hBsel2b.edges[1][1:end-1], hBsel2b.weights, "-")
xlabel("\$E_B\$")


subplot(2, 2, (3, 4))

hABsel2b = fit(Histogram, (sel2b.EAc, sel2b.EBc), (0:10:1000, 0:10:1000))
heatmap(hABsel2b.edges[1], hABsel2b.edges[2], hABsel2b.weights)
xlabel("E_B (keV)")
ylabel("E_A (keV)")

Widmo detektora A wygląda poprawnie, ale w detektorze B mamy tylko szum w okolicy zera.

Aby wyeliminować przypadkowe zdarzenia możemy zadać warunek oparty o dwuwymiarowy wykres. Zarówno w osi X jak i Y za maksimum ciągną się "ogony" związane z rozproszeniami Comptona, ale także możemy mieć zdarzenia gdzie w obydwu detektorach zarejestrowano tylko rozproszenie. Możemy zarządać, aby dobre zdarzenie miało poprawną różnicę czasową oraz aby energia kwantu była powyżej pewnego progu. Z widma detektora A dla czasów bliskich zera widać, że poniżej 100 keV następuje ucięcie, a poniżej tego progu liczba zliczeń gwałtownie spada. Zastosujemy taki sam warunek dla detektora B.

sel3 = df[(-5.0 .< df.tA - df.tB .< 5.0) .& (100 .< df.EAc .< 550) .& (100 .< df.EBc .< 550), :]
subplot(2, 2, 1)
hAsel3 = fit(Histogram, sel3.EAc, 0:10:1000)
plot(hAsel3.edges[1][1:end-1], hAsel3.weights, "-")
xlabel("\$E_A\$")

subplot(2, 2, 2)
hBsel3 = fit(Histogram, sel3.EBc, 0:10:1000)
plot(hBsel3.edges[1][1:end-1], hBsel3.weights, "-")
xlabel("\$E_B\$")

subplot(2, 2, 3)
tABsel3 = fit(Histogram, sel3.tA - sel3.tB, -50:0.5:50)
plot(tABsel3.edges[1][1:end-1], tABsel3.weights, "-")

subplot(2, 2, 4)

hABsel3 = fit(Histogram, (sel3.EAc, sel3.EBc), (0:10:1000, 0:10:1000))
heatmap(hABsel3.edges[1], hABsel3.edges[2], hABsel3.weights)
xlabel("E_B (keV)")
ylabel("E_A (keV)")

Dzięki takiej selekcji danych otrzymaliśmy 5 razy więcej dobrych zdarzeń niż za pomocą zwykłego warunku na energię, jednocześnie mając pewność, że zredukowaliśmy przypadkowe zdarzenia, które mogą redukować rozdzielczość przestrzenną pomiaru. Dzięki większej statystyce eksperyment może trwać odpowiednio krócej lub być dokładniejszy jeżeli zdecydujemy się mierzyć przez ten sam czas. W praktyce medycznej natomiast pacjent może otrzymać odpowiednio mniejszą dawkę promieniotwórczego preparatu, co zmniejsza szanse skutków ubocznych, przy jednoczesnych zachowaniu dokładności obrazowania.

W powyższym przykładzie zastosowaliśmy metodę eksploracji danych. Wiele procedur powtarza się na zasadzie kopiuj-wklej. Oczywiście następnym etapem analizy byłoby przygotowanie programu, gdzie takie czynności zostałyby zebrane w funckję i możliwa byłaby automatyczna analiza wszystkich danych pomiarowych.

CC BY-SA 4.0 Krzysztof Miernik. Last modified: December 04, 2023. Website built with Franklin.jl and the Julia programming language.