Wnioskowanie statystyczne
Jednym z elementów analizy danych jest opisanie uzyskanych wyników eksperymentalnych (pomiarów, obserwacji) za pomocą modelu, który pozwoliłby na przewidywanie zachowania się zjawiska czy układu w przyszłości. Pewne zjawiska można opisać analitycznie za pomocą funkcji lub równań (zwykłych, różniczkowych, całkowych); ewentualnie takie zagadnienie można rozwiązać numerycznie.
W takim przypadku mamy do czynienia ze zjawiskiem deterministycznym. Nie ogranicza nas to do mechaniki klasycznej - deterministyczne mogą być nie tylko takie parametry jak położenie, czy pęd, ale także takie jak funkcja falowa. Znając funkcję falową układu w dowolnym momencie, oraz działające siły, jesteśmy w stanie wyznaczyć stan układu w dowolnym czasie. Funkcja falowa przekłada się oczywiście na wszelkie inne informacje np. prawdopodobieństwo znalezienia cząstki w danym stanie.
Są jednak zagadnienia, które z natury mają charakter statystyczny. W niektórych przypadkach nie umiemy opisać rzeczywistości i wyprowadzić rozkładu statytycznego z bardziej pierwotnych zasad. Czasami świadomie wybieramy fenemenologiczną drogę, ponieważ rozwiązanie problemu jest zbyt czasochłonne lub nie jest potrzebne. W przypadku fenemenologicznego opisu bazujemy na obserwacjach, na ich podstawie tworzymy model (np. opisując statystyczny rozkład jakiegoś parametru funkcją). W przypadku tego podejścia nie wiemy do końca jaki powinien być rozkład (czasami możemy mieć pewne przesłanki, ograniczenia itp.), więc jego wyboru musimy dokonać na podstawie wnioskowania statystycznego poprzez porównanie zaproponowanych modeli.
Spróbujmy wygenerować dane ze znanego nam rozkładu, a potem porównać wyniki dopasowania różnych rozkładów i na tej podstawie dokonać wyboru modelu.
W Julii biblioteka Distributions zawiera bardzo bogatą kolekcję rozkładów prawdopodobieństwa i związanych z nimi narzędzi.
using Distributions
using Random
using StatsBase
using GRUtils
Random.seed!(251)
data = rand(Gamma(10.0, 2.0), 500)Figure((800, 600), "pix")
h1 = fit(Histogram, data, 0:0.5:50)
stairs(h1.edges[1][1:end-1], h1.weights)
hold(true)
h2 = fit(Histogram, data, 0:1:50)
stairs(h2.edges[1][1:end-1], h2.weights)
h3 = fit(Histogram, data, 0:2:50)
stairs(h3.edges[1][1:end-1], h3.weights)Zanim przejdziemy do opisywania wyników rozkładami, powinniśmy utworzyć z nich funkcję gęstości prawdopodobieństwa. Nasze histogramy do tej pory zawierały liczbę zliczeń w danym przedziale, zmieniając szerokość przedziału binowania zmieniamy kształt krzywej.
Aby temu zapobiec musimy stworzyć rozkład gęstości: podzielić każdy bin przez sumę zdarzeń oraz przez szerokość binu. W naszym przypadku wszystkie są tej samej szerokości więc łatwo zrobić tę operację ręcznie. W bardziej ogólnym przydku gdy biny mogą mieć różną szerokość można użyć funkcji normalize z biblioteki LinearAlgebra
using LinearAlgebra
hold(false)
h1 = fit(Histogram, data, 0:0.5:50)
h1 = normalize(h1, mode=:pdf)
stairs(h1.edges[1][1:end-1], h1.weights)
hold(true)
h2 = fit(Histogram, data, 0:1:50)
h2 = normalize(h2, mode=:pdf)
stairs(h2.edges[1][1:end-1], h2.weights)
h3 = fit(Histogram, data, 0:2:50)
h3 = normalize(h3, mode=:pdf)
stairs(h3.edges[1][1:end-1], h3.weights)Tak przygotowane dane możemy porównywać z funkcjami pdf (probability density function). Zaczniemy od dopasowania metodą najmniejszych kwadratów. Spróbujemy opisać dane za pomocą rozkładu normalnego, gamma i Cauchy'ego
using LsqFit
Figure((800, 600), "pix")
h = fit(Histogram, data, 0:1:50)
hn = normalize(h, mode=:pdf)
plot(hn.edges[1][1:end-1], hn.weights, "o")
hold(true)
n(x, p) = pdf.(Normal(p...), x)
c(x, p) = pdf.(Cauchy(p...), x)
g(x, p) = pdf.(Gamma(p...), x)
fn = curve_fit(n, hn.edges[1][1:end-1] .+ 0.5, hn.weights, [10.0, 1.0])
xf = 0:0.1:50
plot(xf, n(xf, fn.param), "-")
fc = curve_fit(c, hn.edges[1][1:end-1] .+ 0.5, hn.weights, [10.0, 1.0])
plot(xf, c(xf, fc.param), "-")
fg = curve_fit(g, hn.edges[1][1:end-1] .+ 0.5, hn.weights, [10.0, 1.0])
plot(xf, g(xf, fg.param), "-")
legend("Data", "Normal", "Cauchy", "Gamma")
hold(false)
display(gcf())Jak wybrać najlepszy model? W fizyce często automatycznie (i bez zastanowienia) posługujemy się testem Chi-kwadrat. Ten test można znaleźć w bibliotece HypothesisTests. Ze względu na jego konstrukcję można go stosować gdy porównujemy liczbę obserwowanych przypadków w pewnych kategoriach z modelem przewidującym prawdopodobieństwo ich zajścia.
Wykonując test porównamy liczby zliczeń dla komórek histogramu (uwaga - nie gęstość prawdopodobieństwa!), z gęstością wyznaczoną w modelach. Ta ostatnia wielkość powinna sumować się do jedności, ale ze względu na dyskretne przedziały, ucięcia zakresu i zaokrąglenia nie jest to koniecznie prawdą. Dlatego musimy znormalizować ten parametr.
using HypothesisTests
using Printf
chin = ChisqTest(h.weights, normalize(n(h.edges[1][1:end-1].+0.5, fn.param), 1));
chic = ChisqTest(h.weights, normalize(c(h.edges[1][1:end-1].+0.5, fc.param), 1));
chig = ChisqTest(h.weights, normalize(g(h.edges[1][1:end-1].+0.5, fg.param), 1));
println(chic)
println("Χ² (normal) = ", @sprintf("%.2f", chin.stat))
println("Χ² (Cauchy) = ", @sprintf("%.2f", chic.stat))
println("Χ² (gamma) = ", @sprintf("%.2f", chig.stat))Dopasowywanie metodą najmniejszych kwadratów i test to oczywiście nie jedyna metoda wyboru modelu.
Inną techniką wyboru parametrów rozkładu jest metoda największej wiarygodności, która polega na maksymalizacji funkcji wiarygodności - w pojedynczym przypadku obserwacji danej próby, dla wielu prób będzie to iloczyn prawdopodobieństw (stąd często wykorzystywany jest logarytm funkcji wiarygodności).
Biblioteka Distributions posiada funkcję fit, która zwróci nam najbardziej prawdopodobne parametry rozkładu znalezione metodą największej wiarygodności (zwykle, można wymusić stosując fit_mle, ale nie każdy rozkład jest zaimplementowany w procedurze maksymalizacji).
pn = params(fit_mle(Normal, data))
pc = params(fit(Cauchy, data))
pg = params(fit_mle(Gamma, data))plot(hn.edges[1][1:end-1], hn.weights, "o")
hold(true)
xf = 0:0.1:50
plot(xf, n(xf, pn), "-")
plot(xf, c(xf, pc), "-")
plot(xf, g(xf, pg), "-")
legend("Data", "Normal", "Cauchy", "Gamma")
hold(false)
display(gcf())
chin = ChisqTest(h.weights, normalize(n(h.edges[1][1:end-1].+0.5, pn), 1));
chic = ChisqTest(h.weights, normalize(c(h.edges[1][1:end-1].+0.5, pc), 1));
chig = ChisqTest(h.weights, normalize(g(h.edges[1][1:end-1].+0.5, pg), 1));
println("Χ² (normal) = ", @sprintf("%.2f", chin.stat))
println("Χ² (Cauchy) = ", @sprintf("%.2f", chic.stat))
println("Χ² (gamma) = ", @sprintf("%.2f", chig.stat))Inną ciekawą obserwacją jest fakt, że metoda najmniejszych kwadratów nie minimalizuje i wynik z metody największej wiarygodności jest inny (szczególnie dla rozkładu normalnego). Korzystając z kryterium moglibyśmy wybrać model Cauchy'ego jako najlepszy w tym przypadku, a Gamma jest zdecydowanie gorszy.
Zanim przejdziemy do innej metody wyboru modelu, narysujemy jak wygląda funkcja wiarygodności dla badanych rozkładów. Wygodny do stosowania jest logarytm tej funkcji. Dla dowolnego rozkładu można ją policzyć w następujący sposób
function llike(dist, x, pars)
ll = 0
for xi in x
ll += logpdf(dist(pars...), xi)
end
if ll == Inf || ll == -Inf
return prevfloat(typemax(Float64))
end
return -ll
endFunkcja logpdf liczy logarytm rozkładu gęstości prawdopodobieństwa. Jeżeli wartość funkcji wyjdzie nam Inf (na przykład dla pdf = 0), to zamieniamy ją na najbliższą liczbę Float64 (czyli bardzo dużą). Wreszcie zwracamy minus wartość ponieważ zwykle procedury znajdują minimum, a nie maksimum.
Wykorzystamy tę funkcję do stworzenia mapy wartości wiarygodności.
m = LinRange(0.1, 30, 64) |> collect
s = LinRange(0.1, 10, 64) |> collect
yn = zeros(size(m)[1], size(s)[1])
yc = zeros(size(m)[1], size(s)[1])
yg = zeros(size(m)[1], size(s)[1])
for j in 1:size(s)[1]
for i in 1:size(m)[1]
yn[i, j] = llike(Normal, data, [m[i], s[j]])
yc[i, j] = llike(Cauchy, data, [m[i], s[j]])
yg[i, j] = llike(Gamma, data, [m[i], s[j]])
end
end
yn = yn .- minimum(yn)
yc = yc .- minimum(yc)
yg = yg .- minimum(yg)
z = [0; 1; 2; LinRange(5, 1000, 7)]
colormap("terrain")
Figure((800, 1200), "pix")
subplot(3, 1, 1)
contourf(s, m, yn, z)
oplot([pn[2]], [pn[1]], "ro")
oplot([fn.param[2]], [fn.param[1]], "rx")
subplot(3, 1, 2)
contourf(s, m, yc, z)
oplot([pc[2]], [pc[1]], "ro")
oplot([fc.param[2]], [fc.param[1]], "rx")
subplot(3, 1, 3)
contourf(s, m, yg, z)
oplot([pg[2]], [pg[1]], "ro")
oplot([fg.param[2]], [fg.param[1]], "rx")
display(gcf())W przedstawionym zakresie każdy rozkład posiada wyraźne minimum. Miejsce gdzie różnica między minimum wynosi 1 (pierwsza poziomica), pozwala na wyznaczenie niepewności danego parametru. W przypadku rozkładu normalnego i Cauchy nie widać między parametrami korelacji, więc mamy poziome elipsy. Dla rozkładu gamma parametry są silnie skorelowane i minimum tworzy długi wąski wąwóz.
Problem wyboru modelu jest jednym z najtrudniejszych zagadnień statystyki. W latach 70-tych Hirotugu Akaike sformuował powszechnie obecnie stosowane kryterium oparte o teorię informacji. Każdy model jest tylko przybliżeniem i pewne informacje zostaną w nim utracone. Miara tego ile informacji została stracona może być wykorzystana do wyboru modelu: ten, który zachowa jej najwięcej zostanie wybrany jako najlepszy. Wzór jest następujący
gdzie to liczba parametrów modelu, a to maksimum funkcji wiarygodności.
Kryterium ma jedynie sens porównywania względnego modeli. Wielkość
określa prawdopodobieństwo, że model zminimalizuje utratę informacji w porównaniu do najlepszego modelu.
W naszym przypadku dla wszystkich modeli, a funkcja llike zwraca wynik ze znakiem minus, więc porównujemy następujące wyrażenia
aic_n = 4 + 2 * llike(Normal, data, pn)
aic_c = 4 + 2 * llike(Cauchy, data, pc)
aic_g = 4 + 2 * llike(Gamma, data, pg)
bestaic = min(aic_n, aic_c, aic_g)
println("ΔAIC Normal = ", aic_n - bestaic)
println("ΔAIC Cauchy = ", aic_c - bestaic)
println("ΔAIC Gamma = ", aic_g - bestaic)@printf("P cauchy %.3e \n", exp((aic_g - aic_c) / 2))
@printf("P normal %.3e \n", exp((aic_n - aic_c) / 2))Nie mamy wątpliwości, że kryterium AIC wskazuje na model Gamma!
Oczywiście wyniki będą zależeć od danej próby i od jej rozmiaru. Możemy zbadać skuteczność metody wyboru modelu opartą o chi-kwadrat oraz o AIC dla wielu próbek i sprawdzić jak skuteczność () zależy od ich rozmiaru ().
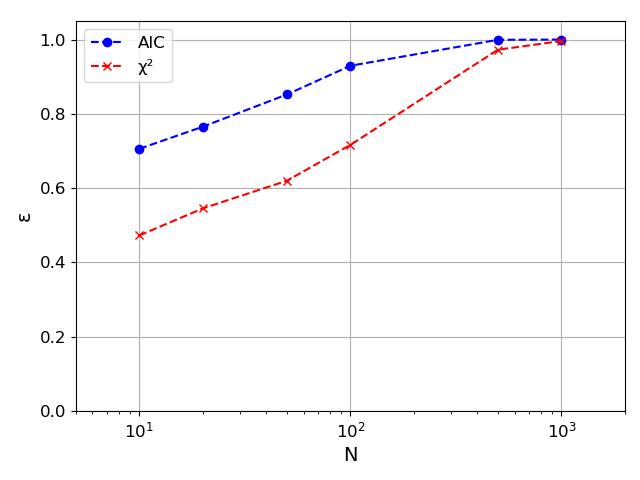
Jeżeli przyjrzymy się dokładniej źródle problemów z metodą opartą o dopasowanie, okaże się, że problem powstaje jeżeli mamy zdarzenia w ogonie rozkładu. Metoda oparta o najmniejsze kwadraty jest mało czuła na takie przypadki, ponieważ jest ich zawsze niewiele. W wartościach bezwzględnych różnica jest mała i bardziej "opłaca" się dobrać parametry rozkładu do najbardziej prawdopodobnych wartości. Tymczasem w metodzie MLE mało prawdopodobne zdarzenia z ogona może mieć duże znaczenie dla parametrów, bo przy ich innym doborze prawdopodobieństwo jego zajścia gwałtownie (eksponencjalnie) maleje i "opłaca" się tak dobrać parametry by zachować sensowne prawdopodobieństwo ich pojawienia się.
Random.seed!(103)
data = rand(Gamma(10.0, 2.0), 1000)
Figure((800, 1200), "pix")
h = fit(Histogram, data, nbins=50)
hn = normalize(h, mode=:pdf)
subplot(3, 1, 1)
plot(hn.edges[1][1:end-1], hn.weights, "o")
hold(true)
xf = h.edges[1][1]:0.1:h.edges[1][end]
println()
fg = curve_fit(g, hn.edges[1][1:end-1], hn.weights, [10.0, 1.0])
plot(xf, g(xf, fg.param), "g-")
pg = params(fit_mle(Gamma, data))
plot(xf, g(xf, pg), "r--")
ylog(true)
ylim(5e-4, 1e-1)
subplot(3, 1, 2)
plot(hn.edges[1][1:end-1], hn.weights - g(hn.edges[1][1:end-1], fg.param), "bo", markersize=0.5)
hold(true)
plot(hn.edges[1][1:end-1], hn.weights - g(hn.edges[1][1:end-1], pg), "rs", markersize=0.5)
ylim(-0.02, 0.02)
subplot(3, 1, 3)
plot(hn.edges[1][1:end-1], (hn.weights - g(hn.edges[1][1:end-1], fg.param)) ./ g(hn.edges[1][1:end-1], fg.param), "bo", markersize=0.5)
hold(true)
plot(hn.edges[1][1:end-1], (hn.weights - g(hn.edges[1][1:end-1], pg)) ./ g(hn.edges[1][1:end-1], pg), "rs", markersize=0.5)
ylim(-5, 5)
display(gcf())Zadanie
Korzystając z bazy NASA Power przeanalizować rozkład prędkości wiatru na wysokości 10 m. Dane powinny dotyczyć co najmniej 10 lat.
Z biblioteki Distributions wybrać modele, które przypominają uzyskany rozkład. Wybrać najlepszy model korzystając z kryterium Akaike i za pomocą dopasowania rozkładu.
Wyniki porównać z najczęściej stosowanymi modelami https://www.sciencedirect.com/science/article/abs/pii/S1364032119304988
using DataFrames
using CSV
df = DataFrame(CSV.File("wind.csv", header=15, delim=",", ignorerepeated=true))Innym zagadnieniem jakie możemy napotkać to testowanie czy dane próby są ze sobą zgodne (czy pochodzą z tego samego rozkładu). Procedura jest następująca
Stawiamy hipotezę zerową (np. dane pochodzą z tego samego rozkładu),
Wybieramy test, który bazuje na jakiejś statystyce (np. test K-S wyznacza maksimum różnic dystrybuanty)
Ustalamy poziom istotności - np. uznajemy, że przyjmujemy, że jeżeli wyliczone prawdodobieństwo, że dane są z tego samego rozkładu jest poniżej 5% to odrzucamy hipotezę, ewentualnie narażając się na popełnienie błędu pierwszego rodzaju - odrzucenie poprawnej hipotezy.
Przeprowadzamy wybrany test
W naszym przypadku, jeżeli chodzi o dane dotyczące wiatru, możemy:
stawiamy hipotezę, że nie ma różnic pomiędzy rozkładem wiatru dla różnych pór roku
ze względu na zmiany klimatu, czy rozkład różni się dla najwcześniejszych i najpóźniejszych lat
Biblioteka HyptothesisTests zawiera kolekcje testów. Jedne z najbardziej popularnych, które możemy użyc w naszej sytuacji to:
test Kołmogorowa-Smirnowa
test Andersona-Darlinga
Obydwa testy występują w wersjach dla jednej próby (tzn. przy teście czy dana populacja pochodzi z danego teoretycznego rozkładu) oraz dla dwóch prób (przy teście pochodzenia populacji z tego samego rozkładu, test A-D może mieć w ogólności prób).
Przetestujmy nasze hipotezy przy poziomie istotności 5%.
ApproximateTwoSampleKSTest(df[in.(df.MO, Ref([12, 1, 2, 3])), :].WS2M, df[in.(df.MO, Ref([4, 5, 6, 7])), :].WS2M)ApproximateTwoSampleKSTest(df[(2000 .<= df.YEAR .<= 2003), :].WS2M, df[(2018 .<= df.YEAR .<= 2021), :].WS2M)KSampleADTest(df[in.(df.MO, Ref([12, 1, 2, 3])), :].WS2M, df[in.(df.MO, Ref([4, 5, 6, 7])), :].WS2M)KSampleADTest(df[(2000 .<= df.YEAR .<= 2003), :].WS2M, df[(2018 .<= df.YEAR .<= 2021), :].WS2M)O ile więc nie mamy podstaw do odrzucenia hipotezy, że rozkład wiatru zmienił się w latach 2018-2021 w stosunku do 2000-2003, to oba testy zdecodywanie odrzucają hipotezę o stałości rozkładu wiatru w ramach roku. Możemy sprawdzić jak wyglądają rozkłady na histrogramach.
h1 = fit(Histogram, df[in.(df.MO, Ref([12, 1, 2, 3])), :].WS2M, 0:0.1:10)
h2 = fit(Histogram, df[in.(df.MO, Ref([4, 5, 6, 7])), :].WS2M, 0:0.1:10)
h3 = fit(Histogram, df[(2000 .<= df.YEAR .<= 2003), :].WS2M, 0:0.1:10)
h4 = fit(Histogram, df[(2018 .<= df.YEAR .<= 2021), :].WS2M, 0:0.1:10)
Figure((800, 800), "pix")
subplot(2, 1, 1)
plot(h1.edges[1][1:end-1], h1.weights, "o", markersize=0.5)
hold(true)
plot(h2.edges[1][1:end-1], h2.weights, "s", markersize=0.5)
legend("Zima", "Wiosna")
subplot(2, 1, 2)
plot(h3.edges[1][1:end-1], h3.weights, "v", markersize=0.5)
hold(true)
plot(h4.edges[1][1:end-1], h4.weights, "^", markersize=0.5)
legend("2000-2003", "2018-2021")
display(gcf())Zadanie
Przetestować hipotezy o:
stałości rozkładu temperatury (porównać wybrane przedziały lat)
stałości rozkładu wiatru dla 4 pór roku (parami)