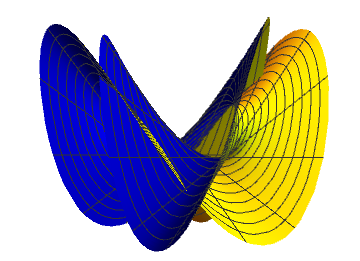
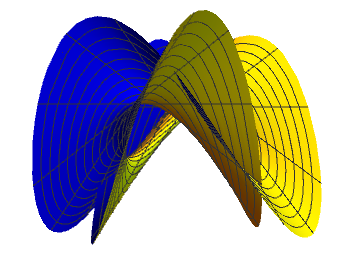
SPHERE EVERSION
Watch on Youtube
Read the math
Published in Differential Geometry and its Applications 64, 59 (2019)
See also: visualization by Marcel Padilla
Download simulation program (C++, OpenGL, platform >= Windows XP)
Sphere eversion means turning inside out a sphere (two-dimensional) in three-dimensional space without pinches or creases but allowing selfintersections. You cannot do it with a circle (one-dimensional) in a two-dimensional plane
DO IT YOURSELF
PAPER

INSTRUCTION
CUT: Cut out 3 sheets of paper with different color on each side (I bought a roll at Flying Tiger Copenhagen) as shown below. All 3 pictures show the same face color side (the other is behind). Make cuts along black lines. Some cuts are INSIDE the sheet, it is easier to cut them later after the first fold.
FOLD: Fold the sheets along green and red lines. Green folds are OUTSIDE (the facing green line becomes the outer fold edge) while red folds are INSIDE (the facing red line becomes the inner fold edge). Remember, inner cuts cross the fold. It is easier to cut the fold. You may swap the roles of the folds but be consistent.
GLUE: The shaded strips are to be glued. Just match the same shapes. In this way the sheet becomes formally a tube although folded.
HAVE FUN: The BEFORE and AFTER sheets can now be unfolded into a tube (and fold back). You need to turn the folds that are not cut by 90 degrees in opposite directions and then just pull the egdes. You can also shift the remaining triangles of the MIDDLE cut to show equivalence to AFTER or BEFORE.
PNG pictures: MIDDLE BEFORE AFTER
NYLON STRINGS
Watch on Youtube
You can model the eversion yourself using plastic tube and nylon string.
Download templates and instructions
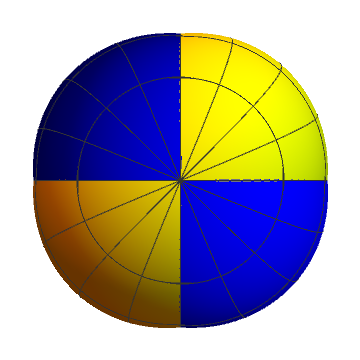
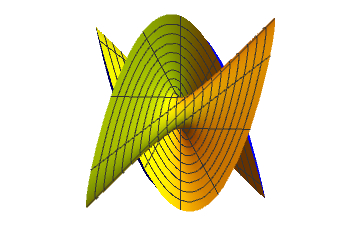
Halfway, Q - point
Central point of the sphere eversion is Morin sufrace, symmetric so that none of sides is priviledged.
Quadruple point: the origin is passed 4 times by the surface. In addition there are 4 saddle-like intersections.
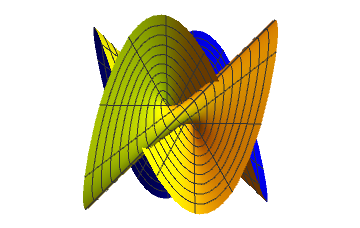
For a moment we send poles to infinity to get a ruled surface

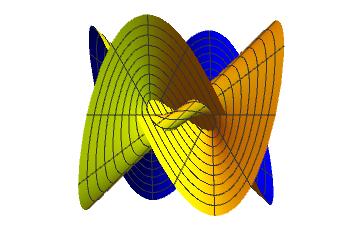
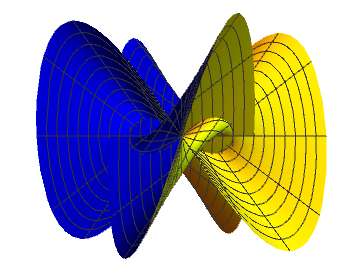
... and close it now


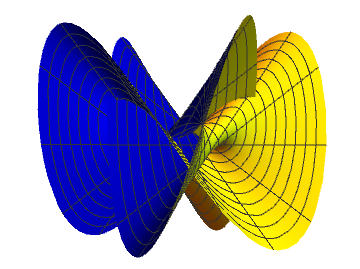
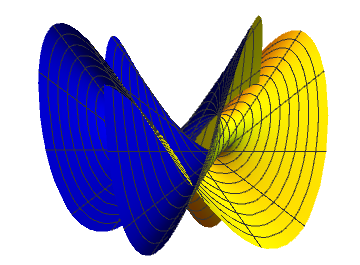
T - point
The quadruple point splits into 4 triple points which finally disappear in pairs


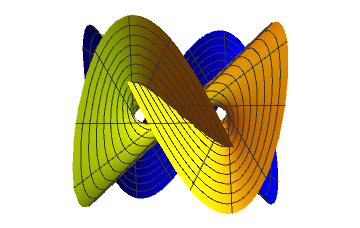
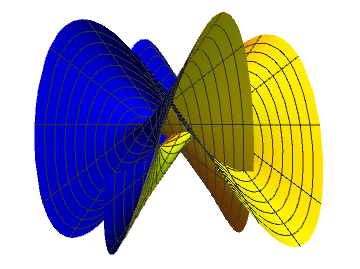
D - point
The central intersection loop gets unentangled and finally disappears at the origin

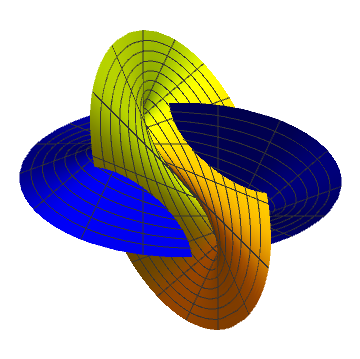
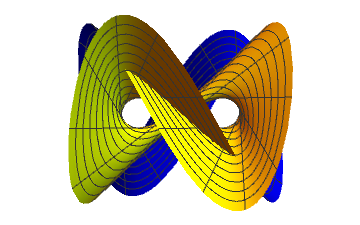
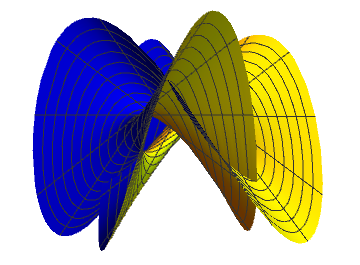
Last stage
A wormhole opens with only simple intersection left