Wnioskowanie Statystyczne

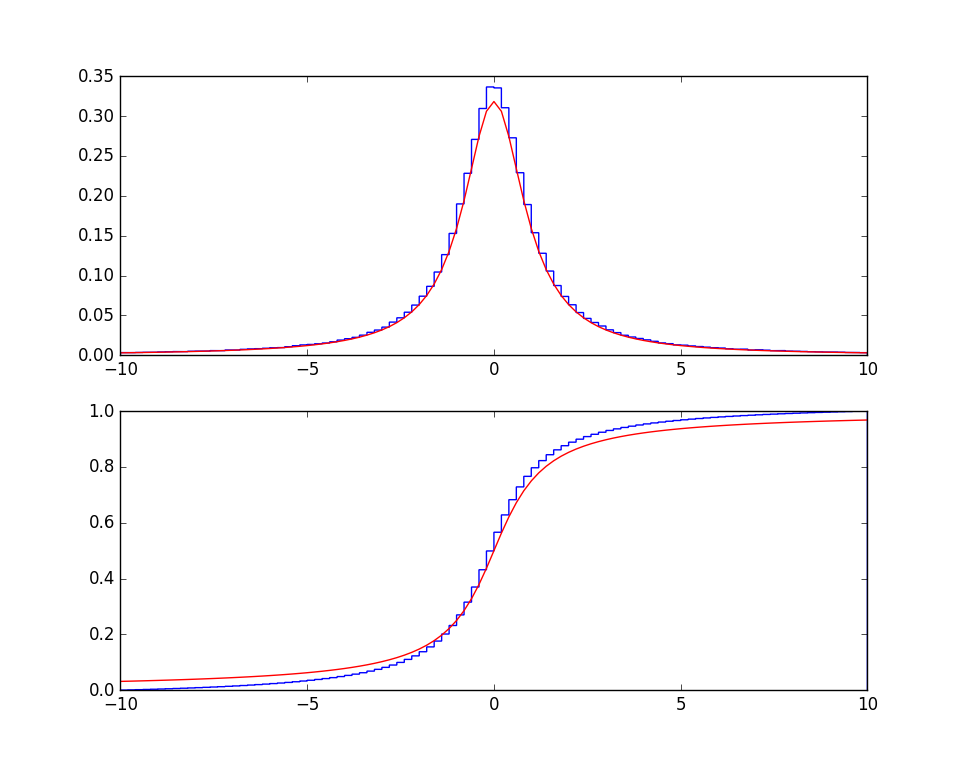
Posiłkując się powyższym przykładem napisz funkcję MyGen(N) dla rozkładu, którego funkcja gęstości prawdopodobieństwa jest dana wzorem: $$f(x) = \frac{1}{\pi (1+x^{2})}.$$ Następnie narysuj dla niego dystrybuantę i dystrybuantę empiryczną na przedziale [-10, 10].

Wyznaczmy najpierw dystrybuantę dla rozkładu f(x): $$F(x)=\int_{-\infty}^{x}\frac{1}{\pi(1+u^2)}du=\frac{1}{\pi} \int_{-\infty}^{x}\frac{1}{1+u^2}du= \left| \frac{1}{1+u^2}=arctg(u) \right| = \left[ \frac{1}{\pi} arctg(u) \right] _{-\infty}^{x}=$$ $$=\frac{1}{\pi} arctg(x) - \frac{1}{\pi} arctg(-\infty) = \frac{1}{\pi} arctg(x) + \frac{1}{\pi} arctg(\infty) =$$ $$\left| \lim_{x\to\infty} arctg(x) = \frac{\pi}{2} \right| = \frac{arctg(x)}{\pi}+\frac{\pi}{2 \pi}=\frac{arctg(x)}{\pi}+\frac{1}{2}$$ Dystrybuanta: $$F(x)=\frac{arctg(x)}{\pi}+\frac{1}{2}$$ Wyznaczmy funkcję odwrotną do dystrybuanty: $$y=\frac{1}{\pi}arctg(x)+\frac{1}{2} \Rightarrow \pi \left( y - \frac{1}{2} \right) = arctg(x) \Rightarrow x=tg \left[ \pi \left( y - \frac{1}{2} \right) \right]$$ Funkcja odwrotna do dystrybuanty: $$F^{-1}(x)= tg \left[ \pi \left( y - \frac{1}{2} \right) \right]$$

import scipy.stats as st
import numpy as np
import pylab as py

def MyGen(size=1):
	x=np.random.random(size) # liczby z generatora jednostajnego na przedziale [0,1)
	y=np.tan(np.pi*(x-1/2))  # korzystamy z metody odwracania dystrybuanty
	return y

x=MyGen(int(1e6))
bins=np.linspace(-10, 10, 101)
py.subplot(211)
py.hist(x, bins, density=True, histtype='step')
py.plot(bins,1./(np.pi*(1+bins**2)), 'r')
py.subplot(212)
py.hist(x, bins, density=True, histtype='step', cumulative=True)
py.plot(bins, np.arctan(bins)/np.pi+0.5, 'r')
py.show()

Rozwiązanie: