Analiza Matematyczna
Ćwiczenia

J. de Lucas

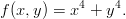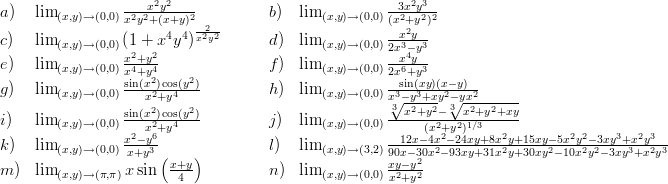
Zadanie 1.  Obliczyć granice następujących funkcji

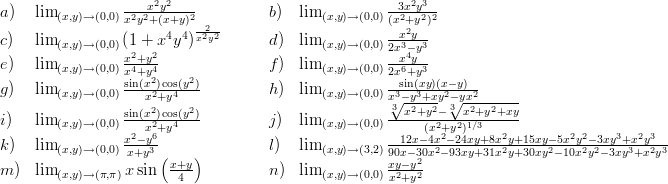
a) lim (x,y)→ (0,0) -22x2y2---2 b) lim (x,y)→ (0,0) -32x2y32-2 xy +(x+y) -2-- (xx+2yy ) c) lim (x,y)→ (0,0)(1 + x4y4) x2y2 d ) lim (x,y)→ (0,0) 2x3--y3- e) lim x2+y2- f ) lim -x4y-- (x,y)→ (0,0) xsi4+ny(x42)cos(y2) (x,y)→ (0,0) 2xs6+iny(3xy)(x-y) g) lim (x,y)→ (0,0) ---x2+y4---- h ) lim (x,y)→ (0,0) x√3--y3+xy2-√yx2------ sin(x2)cos(y2)- 3-x2+y2- 3-x2+y2+xy i) lim (x,y)→ (0,0) x2+y4 j) lim (x,y)→ (0,0) (x2+y2)1∕3 k) lim (x,y)→ (0,0) x2--y36 l) lim (x,y)→ (3,2) -12x-4x22-24xy+8x22y+15xy-25x2y22-32xy3+3x2y32-3- x+y (x+y) 9x0xy--y302x -93xy+31x y+30xy- 10x y -3xy+x y m ) lim (x,y)→ (π,π)xsin 4 n ) lim (x,y)→ (0,0) x2+y2

Zadanie 2.  Zbadać ciągłość następujęcych funkcji

( { exyx-1, dla x ⁄= 0, a) f(x, y) = ( y, dla x = 0, b) f(x, y) = xco2s+(xyy2+)1-, ({ 2 2 [ (--1--) (--1--)] c) f(x, y) = (x + y ) cos x2+y2 + sin x2+y2 , dla (x,y) ⁄= 0, (0, dla (x,y) = 0 ({ sin(xy)- d) f(x, y) = xy , dla xy ⁄= 0, (1, dla xy = 0, ({ log(1+|xy|)- e) f(x, y) = |xy| dla xy ⁄= 0, (1, dla xy = 0,

Zadanie 3.  Obliczyć pochodne cząstkowe rzędu pierwszego następujących funkcji

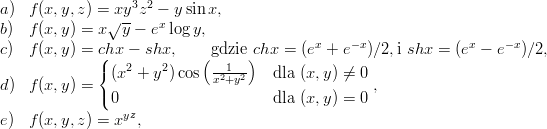
a) f (x, y,z) = xy3z2 - y sin x, √ -- x b) f (x, y) = x y - e log y, x -x x -x c) f (x, y) = c(hx - shx, (gdzie)chx = (e + e )∕2,i shx = (e - e )∕2, {(x2 + y2) cos -21-2 dla (x,y ) ⁄= 0 d) f (x, y) = ( x +y , 0 dla (x,y ) = 0 e) f (x, y,z) = xyz,

Zadanie 4.  Czy funkcja f : ℝ2 → ℝ różniczkowalna w punkcie (x,y) musi być C1 w tym punkcie?

Zadanie 5.  Udowodnij, że funkcja f : ℝ2 → ℝ różniczkowalna w punkcie (x,y) musi być C0 w tym punkcie.

Zadanie 6.  Obliczyć pochodne kierunkowe funkcji

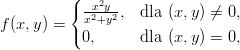
( 2 { x2x+yy2, dla (x,y) ⁄= 0, f(x, y) = ( 0, dla (x,y) = 0,
w kierunku wektora v = (a,b) w punkcie (0, 0).

Zadanie 7.  Zbadaj rózniczkowalność funkcji f(x,y) = |xy| sin(xy).

Zadanie 8. Zbadaj rózniczkowalność funkcji

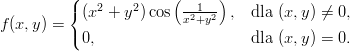
( ( ) { (x2 + y2)cos x2+1y2- , dla (x, y) ⁄= 0, f(x,y) = ( 0, dla (x, y) = 0.

Zadanie 9. Sprawdź, że funkcja

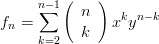
n∑-1( ) fn = n xkyn- k k=2 k
spełnia, że
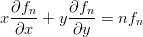
∂fn ∂fn x---- + y---- = nfn ∂x ∂y
dla każdego n ∈ ℕ.

Zadanie 10.Sprawdzić, że funkcja f(x2 + y2 + z2) spełnia, że

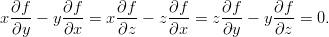
∂f ∂f ∂f ∂f ∂f ∂f x ---- y ---= x--- - z--- = z--- - y ---= 0. ∂y ∂x ∂z ∂x ∂y ∂z

Zadanie 11. Zbadaj rózniczkowalność funkcji

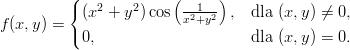
( ( ) { (x2 + y2)cos --1-- , dla (x, y) ⁄= 0, f(x,y) = x2+y2 ( 0, dla (x, y) = 0.

Zadanie 12. Dana funkcja f(x,y) = |xy|, czy spełnia się, że

∂f ∂f [D (hx,hy)f ](x,y ) = ---(x, y)hx + ---(x,y)hy. ∂x ∂y

Zadanie 13. Dana funkcja f ∈ C2(ℝ), napisać wyraż enia

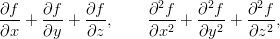
2 2 2 ∂f- ∂f- ∂f- ∂-f- ∂-f- ∂--f ∂x + ∂y + ∂z , ∂x2 + ∂y2 + ∂z2,
w wspórzędnach walcowych {r,ϕ,z}, gdzie
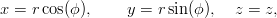
x = rcos(ϕ ), y = r sin(ϕ ), z = z,
w wspólrzędnach sferycznych {r,ϕ,θ} gdzie
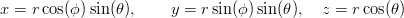
x = r cos(ϕ)sin(θ), y = r sin (ϕ )sin(θ), z = rcos(θ)
w wspólrzędnach elyptycznych {r,ϕ,θ} gdzie
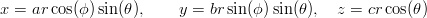
x = arcos(ϕ )sin (θ), y = brsin(ϕ) sin(θ), z = crcos(θ)
i a,b,c > 0.

Zadanie 14.Obliczyć

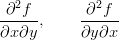
2 2 ∂--f-, ∂--f-- ∂x∂y ∂y∂x
dla funkcji
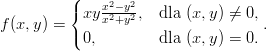
( { xyx2-y2, dla (x,y) ⁄= 0, f (x,y) = x2+y2 . ( 0, dla (x,y) = 0.

Zadanie 15.Czy istnieje funkcja f ∈ C2(ℝ2) taka, że ∂f∕∂x = 2x5 - 6 i ∂f∕∂y = 2y + 5?

Zadanie 16.P. Prawo stanu gazu doskonałego dla dowolnej ilości gazu przyjmuje postać: PV = nRT, gdzie P to ciśnienie gazu, V to objętość gazu, n to ilość moli, T to temperatura i R to stała gazowa. Wykaż, że

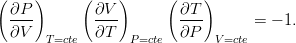
( ∂P ) (∂V ) ( ∂T ) ---- ---- ---- = - 1. ∂V T=cte ∂T P =cte ∂P V=cte

Zadanie 17. Znaleźć i zbadać punkty krytyczne funkcji

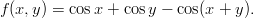
f (x, y) = cosx + cos y - cos(x + y ).

Zadanie 18. Znaleźć i zbadać punkty krytyczne funkcji

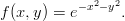
f(x, y) = e-x2-y2.

Zadanie 19. Znaleźć największy i najmniejsze wartości funkcji

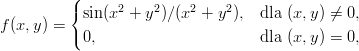
( {sin(x2 + y2)∕(x2 + y2), dla (x,y) ⁄= 0, f(x,y ) = (0, dla (x,y) = 0,
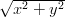na zbiorze K = {(x,y)∣√x2-+--y2- ≤ π∕2}.

Dla tych, którzy nudzą się i chcą coś więcej...

Zadanie 20. Dana funkcja f : ℝn → ℝ typu C1 taka, że f(λx 1,…,λxn) = λnf(x 1,…,xn) dla λ ∈ ℝ, udowodnij, że

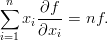
∑n ∂f xi---- = nf. i=1 ∂xi

Zadanie 21. Zbadać punkty krytyczne ciągłej funkcji f : ℝn → ℝ taka, że f(λx 1,…,λxn) = |λ|f(x1,…,xn).

Zadanie 22. Zbadać punkty krytyczne ciągłej funkcji f : ℝ2 → ℝ taka, że f(r cos θ,r sin θ) = f(r cos θ′,r sin θ′) dla wszystkich r,θ,θ′∈ ℝ i ∂f∕∂r > 0.

Zadanie 23. Znaleźć i zbadać punkty krytyczne funkcji

4 4 f(x, y) = x + y .
Cwiczenia i rozwiazania