


Next: Pairing in odd-mass nuclei
Up: Hartree-Fock-Bogoliubov solution of the
Previous: Pairing and the HFB
Regularization of the local pairing interaction
As discussed in Sec. 5, in many HFB applications, pairing
interaction is often assumed to be in the form of the zero-range,
density-dependent force. Calculations using the contact interaction
are numerically simpler, but the pairing gap diverges when the
dimension of the pairing-active space increases for a fixed strength
of the interaction. In roots of this problem is the ultraviolet
divergence of abnormal density for zero-range pairing interaction
[80,81,54]:
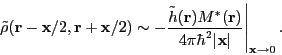 |
(17) |
Consequently, in practical calculations, one has to apply a cutoff
procedure to truncate the pairing-active space of s.p. states
[19,21,37], and the pairing strength has to be
readjusted accordingly. Thus the energy cutoff and the pairing
strength together define the pairing interaction, and this definition
can be understood as a phenomenological introduction of finite range
[21,82,83]. Such a sharp cut-off regularization
is performed in the spirit of the effective field theory, whereupon
contact interactions are used to describe low-energy phenomena while
the coupling constants are readjusted for any given energy cutoff to
account for high energy effects. It has been shown that by an
appropriate renormalization the pairing strength for each value of
the cutoff energy, one practically eliminates the dependence of
various observables on the cutoff parameter[21,54].
Figure 4 illustrates the procedure for the total energy
in the tin isotopes. While for a fixed pairing strength total
energies depend significantly on
the cut-off energy (top), for a fixed pairing gap the
changes obtained with renormalized interactions (bottom) are very
small indeed.
Figure 4:
Total energies in the tin isotopes calculated within the
HFB+SkP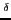 model[21]. Top panel shows the results
for the fixed interaction strength
model[21]. Top panel shows the results
for the fixed interaction strength 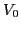 and for several cut-off
energies
and for several cut-off
energies
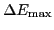 added to the usual
added to the usual
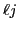 -dependent cut-off energy
-dependent cut-off energy
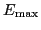 [19].
Bottom panel shows similar results when the values of
[19].
Bottom panel shows similar results when the values of 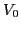 are
renormalized to keep the average neutron pairing gap in
are
renormalized to keep the average neutron pairing gap in 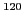 Sn
the same for each
Sn
the same for each
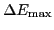 .
.
![\includegraphics[width=0.60\textwidth]{renorm.eps}](img155.png) |
The cutoff energy dependence of the pairing strength can also be
handled by means of a regularization scheme by defining the
regularized local abnormal density
[84,85,80,81,86,87,54]:
![\begin{displaymath}
\tilde\rho_r(\mathbf{r})=\lim_{\mathbf{x}\rightarrow 0}
\lef...
...x}/2,\mathbf{r}+\mathbf{x}/2)-f(\mathbf{r},\mathbf{x})\right],
\end{displaymath}](img156.png) |
(18) |
where 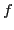 is a regularization counterterm, which removes the
divergence (17) at
is a regularization counterterm, which removes the
divergence (17) at 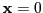 . For cutoff energies high
enough, one can express
. For cutoff energies high
enough, one can express 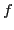 through the s.p. Green's function at
the Fermi level,
through the s.p. Green's function at
the Fermi level,
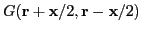 , which also
exhibits a
, which also
exhibits a 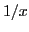 divergence. In practical calculations, one cane use
the Thomas-Fermi (TF) approximation for the local s.p. Green’s
function; this approach has been used with success for a description
of spherical and deformed nuclei
[86,87,54,37]. As demonstrated in
Ref.[54] the differences between pairing renormalization
and regularization procedures are rather small.
divergence. In practical calculations, one cane use
the Thomas-Fermi (TF) approximation for the local s.p. Green’s
function; this approach has been used with success for a description
of spherical and deformed nuclei
[86,87,54,37]. As demonstrated in
Ref.[54] the differences between pairing renormalization
and regularization procedures are rather small.
A combination of the renormalization and regularization methods
described above is the hybrid technique[57] based on the
TF approximation to the non-resonant HFB continuum
[88,89]. This approach is of great practical
interest as it makes it possible to carry out calculations in wide
pairing windows and very large coordinate spaces. In the hybrid
method, the high-energy continuum above the cutoff energy 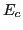 is
divided into the non-resonant part and deep-hole states. While
deep-hole states have to be treated separately, the non-resonant
continuum contribution to HFB densities and fields can be integrated
out by means of the TF approximation. The choice of the cutoff
is
divided into the non-resonant part and deep-hole states. While
deep-hole states have to be treated separately, the non-resonant
continuum contribution to HFB densities and fields can be integrated
out by means of the TF approximation. The choice of the cutoff 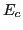 is determined by positions of deep-hole levels[57]; this
information can be obtained by solving the HF problem.
is determined by positions of deep-hole levels[57]; this
information can be obtained by solving the HF problem.



Next: Pairing in odd-mass nuclei
Up: Hartree-Fock-Bogoliubov solution of the
Previous: Pairing and the HFB
Jacek Dobaczewski
2012-07-17
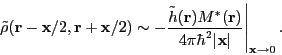
![\includegraphics[width=0.60\textwidth]{renorm.eps}](img155.png)
![]() is
divided into the non-resonant part and deep-hole states. While
deep-hole states have to be treated separately, the non-resonant
continuum contribution to HFB densities and fields can be integrated
out by means of the TF approximation. The choice of the cutoff
is
divided into the non-resonant part and deep-hole states. While
deep-hole states have to be treated separately, the non-resonant
continuum contribution to HFB densities and fields can be integrated
out by means of the TF approximation. The choice of the cutoff ![]() is determined by positions of deep-hole levels[57]; this
information can be obtained by solving the HF problem.
is determined by positions of deep-hole levels[57]; this
information can be obtained by solving the HF problem.