Tetrahedral and Octahedral Symmetry Instabilities

A tendency of generating local minima at non-zero tetrahedral deformation is referred to as the tetrahedral symmetry instability. The corresponding minima

Figure 4: Total energies for $^{156}$Dy nucleus. Top: in function of the quadrupole ( $A20\leftrightarrow \alpha _{20}$) and tetrahedral ( $A32\leftrightarrow \alpha _{32}$) deformations showing a minimum at about 1 MeV above the prolate deformed ground-state. Bottom: similar in function of the quadrupole deformation and the octahedral deformation of the first rank $o_4$. Observe the $\sim$1 MeV barrier separating the two local minima from the ground-state minimum.

are separated with relatively high barriers from the competing, e.g., ground-state minima. It is one of the characteristic features of this mechanism that it is not limited to the tetrahedral doubly-magic nuclei. To the contrary, similar effects are predicted for many nuclei in the vicinity of those doubly magic ones.

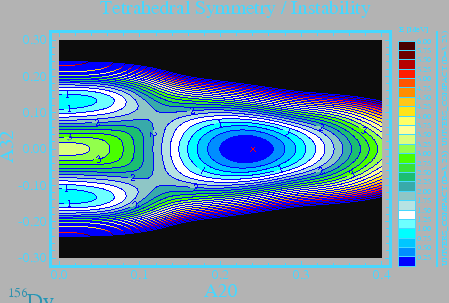
To illustrate this kind of persistent tetrahedral effects, we have chosen the $^{156}$Dy nucleus that has 2 protons in excess of the tetrahedral magic $Z=64$ gap. The corresponding illustration in Fig. 4 was obtained by minimizing the total energy in the 3-dimensional deformation space $(\alpha_{20}, t_{3}\equiv \alpha_{32}, o_{4})$. Each map was constructed by projecting the total energy onto the variable that is not marked on the x- and y-axis ($o_{4}$ for the top frame, $t_{3}$ for the bottome frame). The double minimum structure in the deformation plane $\alpha_{20}$-$\alpha_{32}$ (quadrupole-tetrahedral) is clearly visible. Comparisons show that the tetrahedral deformation brings over 3 MeV of energy gain in this nucleus (as compared to the original energy at the spherical shape). Similarly, the octahedral deformation brings an additional energy gain of about 0.5 MeV. Thus both types of symmetries combine to creating a final minimum with tetrahedral symmetry only, made of the superposition of pure tetrahedral and pure octahedral symmetry components of the nuclear surfaces.

So far we have presented the results based on the calculations employing the non-selfconsistent deformed Woods-Saxon potential; it will be instructive to verify the predictions employing the self-consistent Hartree-Fock method as presented in the next Section.