


Next: Nuclear Surfaces Invariant Under
Up: NUCLEI WITH TETRAHEDRAL SYMMETRY
Previous: Symmetry Arguments - Qualitatively
An ideal tool to study the point-group symmetries and their impact on the
implied properties of the nuclear single-particle spectra are non-selfconsistent realizations of the mean-field approach with parametrized
potentials, as it will be illustrated in Sect. 5 below. One of the very
successful approaches of this kind is provided by the Hamiltonians with the
deformed Woods-Saxon type potentials with its universal1 parametrization that has been in use over many years by now. The
corresponding mean-field Hamiltonian,
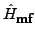 , has the
form,
, has the
form,
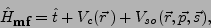 |
(1) |
with the central potential defined by
![\begin{displaymath}
V_c(\vec{r})
\equiv
\frac{\bar{V}}{1+\exp[{{\rm dist}_\Si...
...}\,)/a}]}
+
\frac{1}{2}(1+\tau_3)\,V_{Coulomb}(\vec{r}\,).
\end{displaymath}](img42.png) |
(2) |
Above,
![$\bar{V}\equiv V_0\,[1\pm\kappa(N-Z)/(N+Z)]$](img43.png) (signs: "+" for protons, "-"
for neutrons);
(signs: "+" for protons, "-"
for neutrons); 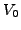 ,
, 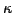 , and
, and 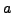 are adjustable parameters and
are adjustable parameters and 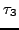 denotes the third component of the isospin. The symbol
denotes the third component of the isospin. The symbol
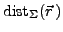 denotes the distance between the current
point position
denotes the distance between the current
point position 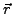 and the nuclear surface
and the nuclear surface 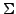 defined in terms of
the spherical harmonics
defined in terms of
the spherical harmonics
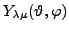 by
by
![\begin{displaymath}
\Sigma:\quad
R(\vartheta,\varphi)
=
R_0 c(\{\alpha\})
\...
...^\star_{\lambda\mu} Y_{\lambda\mu}(\vartheta,\varphi)\bigg].
\end{displaymath}](img50.png) |
(3) |
Above,
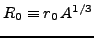 is the nuclear radius parameter and the function
is the nuclear radius parameter and the function
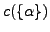 takes care of the nuclear constant volume that is kept
independent of the nuclear deformation. Note that there are effectively three
parameters of the central potential for protons and three for neutrons; they are
denoted as
takes care of the nuclear constant volume that is kept
independent of the nuclear deformation. Note that there are effectively three
parameters of the central potential for protons and three for neutrons; they are
denoted as 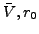 , and
, and 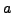 - the central potential depth, radius, and
diffusivity parameters, respectively. It is sometimes convenient to introduce an
alternative representation that replaces
- the central potential depth, radius, and
diffusivity parameters, respectively. It is sometimes convenient to introduce an
alternative representation that replaces 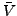 for the protons and a similar
parameter for the neutrons by a suitably chosen set of two parameters. In our
case these are
for the protons and a similar
parameter for the neutrons by a suitably chosen set of two parameters. In our
case these are 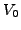 and
and 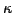 as introduced just below Eq. (2).
as introduced just below Eq. (2).
The spin-orbit potential has the usual form,
![\begin{displaymath}
V_{so}(\vec{r},\vec{p},\vec{s})
\equiv
\lambda_{so} [\nabla V(\vec{r})\wedge\vec{p}\,]\cdot\vec{s},
\end{displaymath}](img54.png) |
(4) |
where 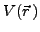 is another Woods-Saxon type deformed potential that differs
from the analogous term in the central potential by the numerical values of the
adjustable constants: here
is another Woods-Saxon type deformed potential that differs
from the analogous term in the central potential by the numerical values of the
adjustable constants: here
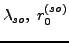 , and
, and 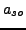 .
.
Beginning with the single-particle spectra obtained by diagonalization of the
above Hamiltonian within the Cartesian harmonic oscillator basis we apply the
macroscopic-microscopic method of Strutinsky using the macroscopic
Yukawa-plus-exponential approach. The formalism that we use here was presented
in details in Refs.[12,13].



Next: Nuclear Surfaces Invariant Under
Up: NUCLEI WITH TETRAHEDRAL SYMMETRY
Previous: Symmetry Arguments - Qualitatively
Jacek Dobaczewski
2006-10-30
![]() , has the
form,
, has the
form,