


Next: Octahedral Symmetry
Up: Interplay Between Tetrahedral and
Previous: Interplay Between Tetrahedral and
The only solutions that are obtained in terms of the spherical harmonics for
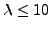 are of the third, seventh and ninth order. For each
multipolarity we find one independent deformation parameter that
characterizes/defines all the other intervening components. We denote those
independent parameters
are of the third, seventh and ninth order. For each
multipolarity we find one independent deformation parameter that
characterizes/defines all the other intervening components. We denote those
independent parameters 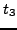 ,
, 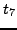 and
and 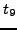 . In the lowest order
(
. In the lowest order
(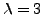 ) we find only two related spherical harmonics intervening, viz. the ones with
) we find only two related spherical harmonics intervening, viz. the ones with 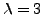 and
and 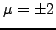 :
:
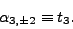 |
(11) |
We find no solutions of order 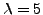 . In the
. In the
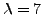 order we find four intervening spherical harmonics, i.e., the ones
corresponding to
order we find four intervening spherical harmonics, i.e., the ones
corresponding to 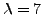 ,
, 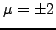 and
and 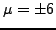 :
:
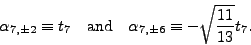 |
(12) |
Finally, for 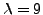 we obtain
we obtain
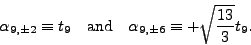 |
(13) |
We may conclude that there exist only very few spherical harmonics of order
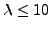 that may be used to construct the surfaces of tetrahedral
symmetry; but even those that are allowed to intervene are strongly correlated
and we have merely 3 independent deformation parameters that characterize the
full parametric freedom within tetrahedral symmetry up to the 10
that may be used to construct the surfaces of tetrahedral
symmetry; but even those that are allowed to intervene are strongly correlated
and we have merely 3 independent deformation parameters that characterize the
full parametric freedom within tetrahedral symmetry up to the 10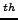 order.
order.



Next: Octahedral Symmetry
Up: Interplay Between Tetrahedral and
Previous: Interplay Between Tetrahedral and
Jacek Dobaczewski
2006-10-30
![]() are of the third, seventh and ninth order. For each
multipolarity we find one independent deformation parameter that
characterizes/defines all the other intervening components. We denote those
independent parameters
are of the third, seventh and ninth order. For each
multipolarity we find one independent deformation parameter that
characterizes/defines all the other intervening components. We denote those
independent parameters ![]() ,
, ![]() and
and ![]() . In the lowest order
(
. In the lowest order
(![]() ) we find only two related spherical harmonics intervening, viz. the ones with
) we find only two related spherical harmonics intervening, viz. the ones with ![]() and
and ![]() :
: