


Next: Isospin mixing
Up: Isospin mixing in nuclei
Previous: Introduction
Theory
The isospin-projected DFT technique [11,12,13]
utilizes the ability of the
self-consistent MF method to properly describe the balance between
the long-range Coulomb force and the short-range nuclear interaction,
represented in this work by the Skyrme-type energy density functional (EDF). To
remove the spurious isospin-symmetry-breaking effects, we use the
standard one-dimensional isospin projection after variation, which
allows us to decompose the Slater determinant 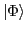 into
good isospin states
into
good isospin states 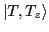 :
:
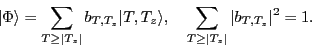 |
(1) |
Here,
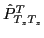 stands for the conventional
one-dimensional isospin-projection operator:
stands for the conventional
one-dimensional isospin-projection operator:
where 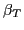 denotes the Euler angle
associated with the rotation operator
denotes the Euler angle
associated with the rotation operator
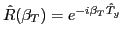 about the
about the 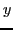 -axis in the isospace,
-axis in the isospace,
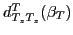 is
the Wigner function [17], and
is
the Wigner function [17], and 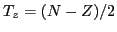 is the third component
of the total isospin
is the third component
of the total isospin 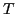 . The normalization factors
. The normalization factors 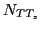 , or
interchangeably the expansion coefficients
, or
interchangeably the expansion coefficients 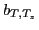 that encode the
isospin content of
that encode the
isospin content of
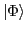 , read:
, read:
where
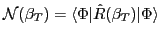 is the so-called overlap kernel. For technical aspects concerning the
calculation of the overlap and Hamiltonian kernels, we refer the reader to
Ref. [13].
The isospin-projected DFT technique utilizes the ability of
the HF solver HFODD [18] to produce fully
symmetry-unrestricted Slater determinants
is the so-called overlap kernel. For technical aspects concerning the
calculation of the overlap and Hamiltonian kernels, we refer the reader to
Ref. [13].
The isospin-projected DFT technique utilizes the ability of
the HF solver HFODD [18] to produce fully
symmetry-unrestricted Slater determinants 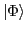 .
.
The isospin projection determines the set of good isospin states
(called the basis in the following), which in the next step is used to rediagonalize
the entire nuclear Hamiltonian, consisting of the kinetic energy, Skyrme EDF,
and the isospin-breaking Coulomb force. The rediagonalization leads to the
eigenstates:
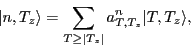 |
(4) |
numbered by index 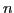 . The amplitudes
. The amplitudes 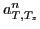 define the degree of
isospin mixing through the so-called isospin-mixing
coefficients (or isospin impurities)
for the
define the degree of
isospin mixing through the so-called isospin-mixing
coefficients (or isospin impurities)
for the 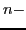 th eigenstate:
th eigenstate:
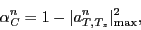 |
(5) |
where
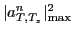 stands for the squared norm of the dominant amplitude in the wave function
stands for the squared norm of the dominant amplitude in the wave function
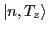 .
It is worth stressing that the isospin projection, unlike particle-number
or angular-momentum projections, is essentially non-singular; hence, it
can be safely used with the local EDFs. The rigorous analytical proof of this useful property can be found in Ref. [13].
.
It is worth stressing that the isospin projection, unlike particle-number
or angular-momentum projections, is essentially non-singular; hence, it
can be safely used with the local EDFs. The rigorous analytical proof of this useful property can be found in Ref. [13].
The combined isospin and angular-momentum projection
leads to the set of states,
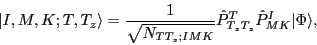 |
(6) |
which form another normalized basis built on 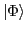 .
Here,
.
Here,
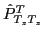 and
and 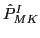 stand for the isospin
and angular-momentum projection operators, respectively, and
stand for the isospin
and angular-momentum projection operators, respectively, and
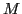 and
and 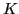 denote the angular-momentum components along
the laboratory and intrinsic
denote the angular-momentum components along
the laboratory and intrinsic 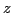 -axes, respectively [19].
Now the problem becomes
more complicated because of the overcompleteness of the basis (6)
related to the
-axes, respectively [19].
Now the problem becomes
more complicated because of the overcompleteness of the basis (6)
related to the 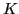 -mixing. This is overcome by performing the rediagonalization
of the Hamiltonian in the so-called collective space, spanned for
each
-mixing. This is overcome by performing the rediagonalization
of the Hamiltonian in the so-called collective space, spanned for
each 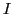 and
and 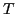 by the natural states,
by the natural states,
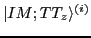 , as
described in Refs. [18,20].
Such a rediagonalization gives the solutions:
, as
described in Refs. [18,20].
Such a rediagonalization gives the solutions:
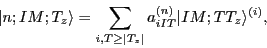 |
(7) |
which are labeled by the index 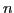 and by the conserved quantum numbers
and by the conserved quantum numbers 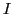 ,
, 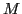 , and
, and
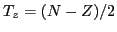 [cf. Eq. (4)].
[cf. Eq. (4)].



Next: Isospin mixing
Up: Isospin mixing in nuclei
Previous: Introduction
Jacek Dobaczewski
2011-02-20
![]() into
good isospin states
into
good isospin states ![]() :
: