In both CHF and CRMF calculations, the set of independent-particle configurations
in nuclei around ![]() Ce was considered. The final sets used in
additivity analysis consisted of 183 and 105 configurations in the
CHF and CRMF variants, respectively. All ambiguous cases, due to
crossings, convergence difficulties, etc., were removed from those
sets. Since the CRMF calculations are more time-consuming than the
CHF ones, the CRMF set is smaller. Nonetheless, the adopted CRMF set is
sufficiently large to provide reliable results. To put things in perspective,
in Ref. [5], where the CHF analysis of additivity principle in the
SD bands of the
Ce was considered. The final sets used in
additivity analysis consisted of 183 and 105 configurations in the
CHF and CRMF variants, respectively. All ambiguous cases, due to
crossings, convergence difficulties, etc., were removed from those
sets. Since the CRMF calculations are more time-consuming than the
CHF ones, the CRMF set is smaller. Nonetheless, the adopted CRMF set is
sufficiently large to provide reliable results. To put things in perspective,
in Ref. [5], where the CHF analysis of additivity principle in the
SD bands of the ![]() mass region was carried out,
74 calculated SD configurations were considered.
mass region was carried out,
74 calculated SD configurations were considered.
Every calculated product-state configuration was labeled using the standard notation in
terms of parity-signature blocks
![]() , where
, where ![]() are the numbers of occupied s.p. orbitals
having parity
are the numbers of occupied s.p. orbitals
having parity ![]() and signature
and signature ![]() . In addition, the s.p. states were labeled
by the Nilsson quantum numbers and signature
. In addition, the s.p. states were labeled
by the Nilsson quantum numbers and signature
![]() of the active orbitals at zero frequency. The orbital identification
is relatively straightforward
when the s.p. levels do not cross (or cross with a small interaction matrix element),
but it can become ambiguous when the crossings with
strong mixing occur. In some cases,
it was necessary to construct diabatic routhians by removing weak interaction at
crossing points. Even with these
precautions, a reliable configuration assignment was not always possible;
the exceptional cases were excluded from the additivity analysis. Clearly,
the likelihood of the occurrence
of level crossings is reduced when the s.p. level density is small, e.g.,
in the vicinity of large shell gaps.
of the active orbitals at zero frequency. The orbital identification
is relatively straightforward
when the s.p. levels do not cross (or cross with a small interaction matrix element),
but it can become ambiguous when the crossings with
strong mixing occur. In some cases,
it was necessary to construct diabatic routhians by removing weak interaction at
crossing points. Even with these
precautions, a reliable configuration assignment was not always possible;
the exceptional cases were excluded from the additivity analysis. Clearly,
the likelihood of the occurrence
of level crossings is reduced when the s.p. level density is small, e.g.,
in the vicinity of large shell gaps.
Large deformed energy gaps develop at high rotational velocity for ![]() =58 and
=58 and ![]() =73
(see Figs. 2 and 3). Therefore, the lowest
SD band (
=73
(see Figs. 2 and 3). Therefore, the lowest
SD band (![]() band) in
band) in ![]() Ce is a natural
choice for the highly deformed core configuration in the
Ce is a natural
choice for the highly deformed core configuration in the ![]()
![]() 130 mass region.
The
additivity analysis was performed at a large rotational frequency of
130 mass region.
The
additivity analysis was performed at a large rotational frequency of ![]() =0.65MeV.
This choice was dictated by the fact that (i) at this frequency the
pairing is already considerably quenched, and (ii) no level crossings appear
in the core configuration around this frequency (cf. Figs. 2 and 3). Moreover, at this frequency, the lowest
neutron
=0.65MeV.
This choice was dictated by the fact that (i) at this frequency the
pairing is already considerably quenched, and (ii) no level crossings appear
in the core configuration around this frequency (cf. Figs. 2 and 3). Moreover, at this frequency, the lowest
neutron ![]() intruder orbital already appears below the
intruder orbital already appears below the ![]() =73 neutron gap
(see Fig. 2). The choice of an odd-even core,
strongly motivated by its doubly
closed character at large deformations/spins, does not impact the
additivity scheme, which is insensitive to the selection of the reference system.
=73 neutron gap
(see Fig. 2). The choice of an odd-even core,
strongly motivated by its doubly
closed character at large deformations/spins, does not impact the
additivity scheme, which is insensitive to the selection of the reference system.
The highly deformed core configuration in ![]() Ce ([18,19,18,18]
Ce ([18,19,18,18]![]() [14,14,15,15]
[14,14,15,15]![]() )
has the following orbital structure:
)
has the following orbital structure:
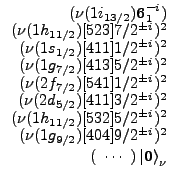 and
and
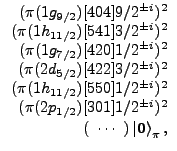 are the neutron and proton vacua, respectively.
The spherical subshells from which the deformed s.p. orbitals emerge
(cf. Fig. 1) are indicated in the front of the Nilsson labels.
are the neutron and proton vacua, respectively.
The spherical subshells from which the deformed s.p. orbitals emerge
(cf. Fig. 1) are indicated in the front of the Nilsson labels.
The Nilsson orbital content of an excited configuration is given in
terms of particle and hole excitations with respect to the core configuration
through the action of particle/hole operators with quantum labels corresponding
to the occupied or emptied Nilsson orbitals. The character of the orbital
(particle or hole) is defined by the position of the orbital with respect to
the Fermi level of the core configuration. It is clear from Fig. 2
that the neutron states
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and ![]() have hole character, while
have hole character, while ![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() , and
, and
![]() have
particle character. In a similar way, the proton orbitals
have
particle character. In a similar way, the proton orbitals
![]() ,
,
![]() ,
,
![]() , and
, and
![]() and
and
![]() can be viewed as holes, while
can be viewed as holes, while
![]() ,
,
![]() ,
,
![]() , and
, and
![]() have particle character (see Fig. 3).
have particle character (see Fig. 3).