


Next: Mean-field calculations with tensor
Up: Tensor densities in the
Previous: Spin-orbit and tensor forces
Within the energy-density approach, one does not relate the EDF to an
average of the two-body force, but one postulates the EDF based on
symmetry conditions only. Then, the most general EDF, depending on the
spin-current densities, reads[4]
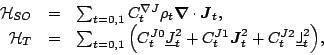 |
(5) |
where the spherical-symmetry condition has been released.
The
standard pseudoscalar
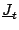 , vector
, vector
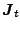 ,
and pseudotensor
,
and pseudotensor
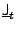 parts of the
spin-current density,[16]
parts of the
spin-current density,[16]
 |
(6) |
are defined as
 |
(7) |
The tensor energy density
 now depends
on six coupling constants,
now depends
on six coupling constants,  ,
, 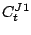 , and
, and 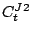 ,
for
,
for 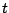 =0,1, and not on two coupling constants,
=0,1, and not on two coupling constants, 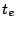 and
and 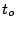 , as in Eq. 3.
Similarly, the SO energy density
, as in Eq. 3.
Similarly, the SO energy density
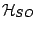 depends now on two coupling constants
depends now on two coupling constants
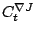 for
for 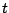 =0,1,
and not on one,
=0,1,
and not on one, 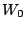 , (the latter generalization has been introduced
and studied in Ref.[17]).
, (the latter generalization has been introduced
and studied in Ref.[17]).
From the symmetry conditions imposed by the spherical, axial, and
reflection symmetries one obtains[18] that:
- 1
- The pseudoscalar densities
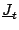 vanish unless the axial or reflection symmetries are broken.
vanish unless the axial or reflection symmetries are broken.
- 2
- The pseudotensor densities
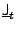 vanish unless the spherical symmetry is broken.
vanish unless the spherical symmetry is broken.
Finally, the gauge-invariance symmetry conditions[4]
require that there are only two gauge-invariant combinations
of the pseudoscalar, vector,
and pseudotensor terms, namely,
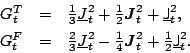 |
(8) |
In such a case, only four out of the six tensor coupling constants are linearly
independent, i.e.,
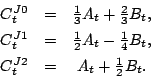 |
(9) |
On the other hand, the averaging of the tensor forces (1)
implies that only two out of the six tensor coupling constants remain
linearly independent, i.e.,
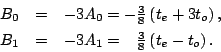 |
(10) |



Next: Mean-field calculations with tensor
Up: Tensor densities in the
Previous: Spin-orbit and tensor forces
Jacek Dobaczewski
2006-04-22
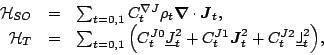
![]() now depends
on six coupling constants,
now depends
on six coupling constants, ![]() ,
, ![]() , and
, and ![]() ,
for
,
for ![]() =0,1, and not on two coupling constants,
=0,1, and not on two coupling constants, ![]() and
and ![]() , as in Eq. 3.
Similarly, the SO energy density
, as in Eq. 3.
Similarly, the SO energy density
![]() depends now on two coupling constants
depends now on two coupling constants
![]() for
for ![]() =0,1,
and not on one,
=0,1,
and not on one, ![]() , (the latter generalization has been introduced
and studied in Ref.[17]).
, (the latter generalization has been introduced
and studied in Ref.[17]).