 |
As in previous studies based on the SLy4 functional,[21,22]
we found that all nuclei considered in this work have spherical
shapes in their ground states. This is because ![]() =184 appears to be
the magic neutron number in most theoretical models based on
the Skyrme approach.[23] Due to the magic character of
=184 appears to be
the magic neutron number in most theoretical models based on
the Skyrme approach.[23] Due to the magic character of ![]() =184
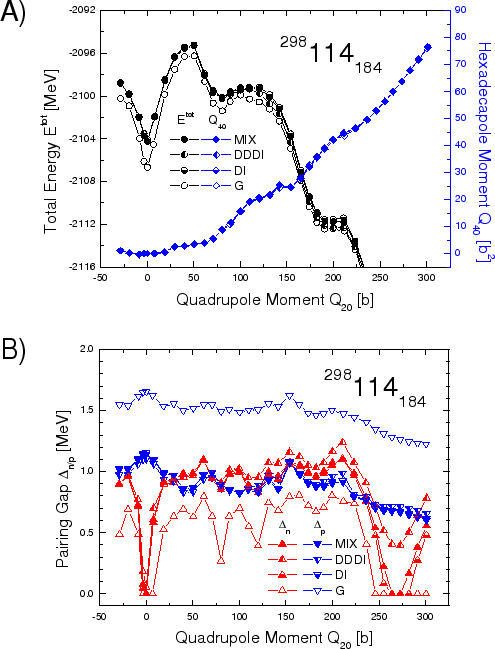
isotones, ground-state neutron pairing gaps calculated in BCS vanish.
The ground-state proton pairing gaps, on the other hand, show considerable
variations with
=184
isotones, ground-state neutron pairing gaps calculated in BCS vanish.
The ground-state proton pairing gaps, on the other hand, show considerable
variations with ![]() .
They are large in the open-shell rutherfordium (
.
They are large in the open-shell rutherfordium (![]() =104), but
in
=104), but
in ![]() =114 the values of
=114 the values of ![]() are considerably reduced. As expected,
proton pairing is much weakened for
are considerably reduced. As expected,
proton pairing is much weakened for ![]() =126 which is predicted to be
semi-magic.[21,22,23]
=126 which is predicted to be
semi-magic.[21,22,23]
The calculated static fission paths have reflection-symmetric
shapes, i.e.,
![]() for all odd multipolarities
for all odd multipolarities
![]() . Furthermore, one can see that irrespective of the pairing
interaction used, the hexadecapole moments are almost identical, and
they gradually increase (from 0 up to about 80b
. Furthermore, one can see that irrespective of the pairing
interaction used, the hexadecapole moments are almost identical, and
they gradually increase (from 0 up to about 80b![]() ) along the
calculated static fission paths. In contrast to
) along the
calculated static fission paths. In contrast to ![]() , the
collective potentials (i.e., total energies
, the
collective potentials (i.e., total energies
![]() as
functions of
as
functions of ![]() ) differ depending on the pairing model
employed. This is particularly evident for
) differ depending on the pairing model
employed. This is particularly evident for ![]() Rf
Rf![]() (Fig. 1A) where the fission barrier calculated within the
SHF+BCS(G) model is significantly higher as compared to those
obtained in the SHF+BCS(
(Fig. 1A) where the fission barrier calculated within the
SHF+BCS(G) model is significantly higher as compared to those
obtained in the SHF+BCS(![]() ) variants. In the case of
) variants. In the case of
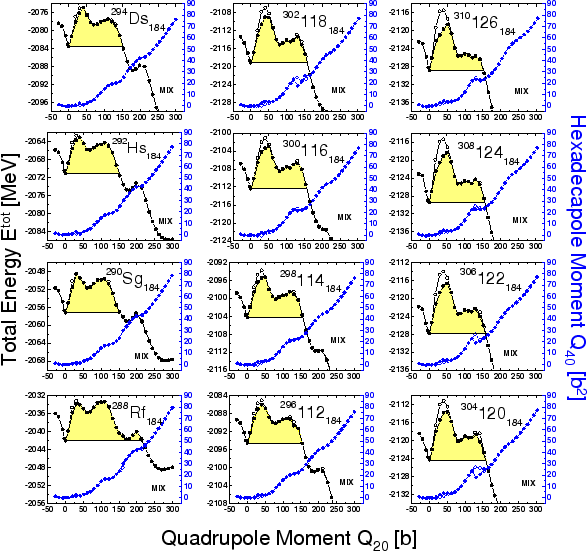
![]() (Fig. 2A), the fission barriers
calculated with the SHF+BCS(G) and SHF+BCS(
(Fig. 2A), the fission barriers
calculated with the SHF+BCS(G) and SHF+BCS(![]() ) interactions
are considerably closer to one another than in the case of
) interactions
are considerably closer to one another than in the case of
![]() Rf
Rf![]() . Furthermore, for
. Furthermore, for
![]() (Fig. 3A), all fission barriers calculated with both
pairing models are almost identical. This can be attributed to the
behavior of proton pairing along the fission paths. Indeed, in
(Fig. 3A), all fission barriers calculated with both
pairing models are almost identical. This can be attributed to the
behavior of proton pairing along the fission paths. Indeed, in
![]() Rf
Rf![]() there is a large systematic difference between
there is a large systematic difference between
![]() values in SHF+BCS(G) and SHF+BCS(
values in SHF+BCS(G) and SHF+BCS(![]() ) variants,
with the seniority-pairing model producing considerably larger
pairing gaps. This difference decreases when going towards
) variants,
with the seniority-pairing model producing considerably larger
pairing gaps. This difference decreases when going towards
![]() in which
in which ![]() obtained within the
SHF+BCS(G) model are much closer to those obtained within the
SHF+BCS(
obtained within the
SHF+BCS(G) model are much closer to those obtained within the
SHF+BCS(![]() ) model. This result indicates that the isospin
dependence of seniority pairing strengths given by Eq. (1) is
too strong and thus unrealistic. Another interesting observation is
that neutron/proton pairing gaps (hence, corresponding potential
energies) calculated within the SHF+BCS(
) model. This result indicates that the isospin
dependence of seniority pairing strengths given by Eq. (1) is
too strong and thus unrealistic. Another interesting observation is
that neutron/proton pairing gaps (hence, corresponding potential
energies) calculated within the SHF+BCS(![]() ) framework are very
similar, regardless of the parameterization variant used (MIX, DDDI
or DI), see Eq. (4).
) framework are very
similar, regardless of the parameterization variant used (MIX, DDDI
or DI), see Eq. (4).
 |