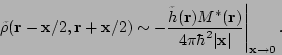Next: Bibliography
Up: Pairing renormalization and regularization
Previous: Summary and Conclusions
Divergence in the Abnormal Density
In the DFT-HFB approach, the starting point is the Energy Density
Functional (EDF)
![$\mathcal{H}[\rho,\tilde\rho]$](img81.png) , where
, where 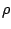 is the
particle density and
is the
particle density and 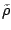 is the abnormal density:
is the abnormal density:
where 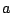 and
and 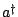 are the particle annihilation and
creation operators, respectively, and
are the particle annihilation and
creation operators, respectively, and 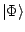 is the HFB
state. In the following, we assume that
is the HFB
state. In the following, we assume that 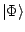 is a product of
the neutron and proton states,
is a product of
the neutron and proton states,
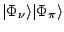 .
Therefore, the neutron and proton wave functions are not coupled, and
in the notation below we can, for simplicity, omit the isospin index
with the understanding that all equations are separately valid for
neutrons and protons.
.
Therefore, the neutron and proton wave functions are not coupled, and
in the notation below we can, for simplicity, omit the isospin index
with the understanding that all equations are separately valid for
neutrons and protons.
For the HFB state 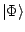 , the particle and abnormal
densities can be written as [12]:
, the particle and abnormal
densities can be written as [12]:
where the two-component quasiparticle wave function
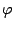 is the solution of the HFB equation:
is the solution of the HFB equation:
| |
|
![$\displaystyle \sum_{\sigma_1}\int d^3\mathbf{r_1}\left[\begin{array}{cc}h_{\mu}...
..._1)&-h_{\mu}(\mathbf{r_2}\sigma_2,\mathbf{r_1}\sigma_1)\end{array}\right]\times$](img96.png) |
|
| |
|
![$\displaystyle \times\left[\begin{array}{c}\varphi_{1i}(\mathbf{r_1}\sigma_1)\\ ...
...(\mathbf{r_2}\sigma_2)\\ \varphi_{2i}(\mathbf{r_2}\sigma_2)\end{array}\right],$](img97.png) |
(20) |
for a given quasiparticle energy 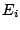 .
.
The HFB equations are a result of variational minimization of the
energy density functional
![$\mathcal{H}[\rho,\tilde\rho]$](img81.png) with the constraint of the
mean value of particles kept constant:
with the constraint of the
mean value of particles kept constant:
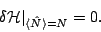 |
(21) |
This condition defines the s.p. Hamiltonian 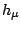 and
the pairing Hamiltonian
and
the pairing Hamiltonian 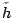 in the HFB equations (20):
in the HFB equations (20):
where 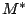 is the effective mass and
is the effective mass and 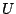 is the self-consistent mean-field potential.
In the following derivations, the spin-orbit term is omitted as unimportant in the regularization scheme, although it is, of course, always included in calculations.
is the self-consistent mean-field potential.
In the following derivations, the spin-orbit term is omitted as unimportant in the regularization scheme, although it is, of course, always included in calculations.
By multiplying the HFB equations (20) by vector
![$[\varphi_{2i}^*,-\varphi_{1i}^*]$](img104.png) , integrating over coordinates and
summing over all the positive energy HFB solutions, one obtains:
, integrating over coordinates and
summing over all the positive energy HFB solutions, one obtains:
![$\displaystyle {\sum_{E_i>0,\sigma_2} E_i\int d^3\mathbf{r_2}
\left[\begin{array...
...mathbf{r_2}\sigma_2)\\ \varphi_{2i}(\mathbf{r_2}\sigma_2)
\end{array}\right]=}$](img105.png) |
| |
|
![$\displaystyle =\sum_{E_i>0,\sigma_1\sigma_2} \int d^3\mathbf{r_1}d^3\mathbf{r_2...
...(\mathbf{r_1}\sigma_1)\\ \varphi_{2i}(\mathbf{r_1}\sigma_1)
\end{array}\right]$](img106.png) |
(24) |
i.e.,
Since for every HFB solution
![$([\varphi_{1i},\varphi_{2i}],E_i)$](img110.png) there
exists also an orthogonal solution
there
exists also an orthogonal solution
![$([\varphi_{2i},-\varphi_{1i}],-E_i)$](img111.png) ,
the left-hand side of Eq. (25) vanishes as a sum over
scalar products of orthogonal wave functions.
,
the left-hand side of Eq. (25) vanishes as a sum over
scalar products of orthogonal wave functions.
For local and spin-independent Hamiltonians 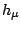 and
and 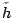 ,
Eqs. (23) and (23) read
,
Eqs. (23) and (23) read
Note that for an attractive pairing force, the local pairing potential
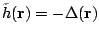 is negative,
where
is negative,
where
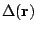 is the standard position-dependent pairing gap.
By defining function
is the standard position-dependent pairing gap.
By defining function
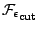 as
as
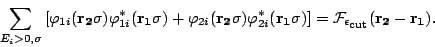 |
(28) |
and using expression (19) for the abnormal density, one obtains
after integrating the kinetic-energy term by parts:
where
and
When the summation over positive quasiparticle energies is extended to infinity,
the completeness relation implies that
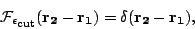 |
(34) |
and the only term in Eq. (29) capable of canceling out this singularity
is
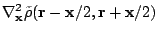 . Therefore,
the Laplacian of the abnormal density
. Therefore,
the Laplacian of the abnormal density
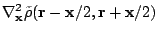 must be singular
at
must be singular
at 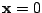 . Moreover, using the expression
. Moreover, using the expression
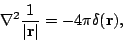 |
(35) |
it is clear that due to the zero-range pairing interaction
abnormal density 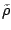 has an ultraviolet
has an ultraviolet 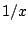 divergence:
divergence:
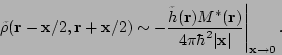 |
(36) |



Next: Bibliography
Up: Pairing renormalization and regularization
Previous: Summary and Conclusions
Jacek Dobaczewski
2006-01-19
![]() , where
, where ![]() is the
particle density and
is the
particle density and ![]() is the abnormal density:
is the abnormal density:
![]() , the particle and abnormal
densities can be written as [12]:
, the particle and abnormal
densities can be written as [12]:
![]() with the constraint of the
mean value of particles kept constant:
with the constraint of the
mean value of particles kept constant:
![]() , integrating over coordinates and
summing over all the positive energy HFB solutions, one obtains:
, integrating over coordinates and
summing over all the positive energy HFB solutions, one obtains:
![$\displaystyle {\sum_{E_i>0,\sigma_2} E_i\int d^3\mathbf{r_2}
\left[\begin{array...
...mathbf{r_2}\sigma_2)\\ \varphi_{2i}(\mathbf{r_2}\sigma_2)
\end{array}\right]=}$](img105.png)
![$\displaystyle =\sum_{E_i>0,\sigma_1\sigma_2} \int d^3\mathbf{r_1}d^3\mathbf{r_2...
...(\mathbf{r_1}\sigma_1)\\ \varphi_{2i}(\mathbf{r_1}\sigma_1)
\end{array}\right]$](img106.png)
![]() and
and ![]() ,
Eqs. (23) and (23) read
,
Eqs. (23) and (23) read