|
To complete the presentation of our results, we here formulate and discuss the separability rule, by which our planar (2D) and chiral (3D) HF TAC solutions turn out to be simple superpositions of independent HF PAC (1D) rotations about 2 or 3 principal axes, respectively.

|
Take, for instance, the total alignments on the principal axes,
![]() , where
, where ![]() , as functions of the corresponding
components of the angular frequency. Such quantities were examined in
Section 3.4 for the PAC calculations, but they can be
equally well extracted for the planar and chiral solutions. A
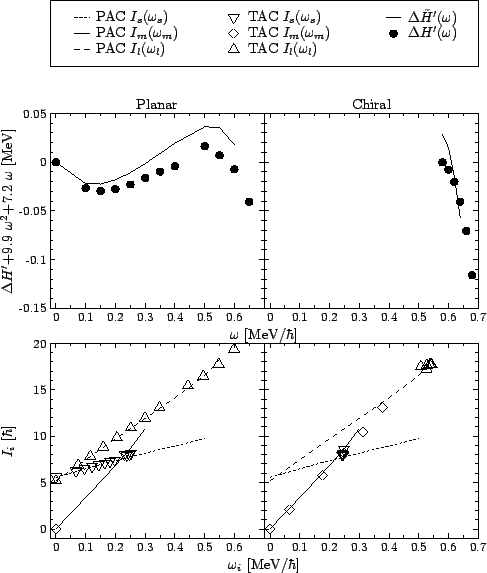
comparison of the PAC and TAC results in
, as functions of the corresponding
components of the angular frequency. Such quantities were examined in
Section 3.4 for the PAC calculations, but they can be
equally well extracted for the planar and chiral solutions. A
comparison of the PAC and TAC results in ![]() La is shown in the
lower part of Fig. 11 for the
La is shown in the
lower part of Fig. 11 for the ![]() variant of
calculations with the SkM* force. The PAC values of
variant of
calculations with the SkM* force. The PAC values of ![]() ,
, ![]() , and
, and
![]() are plotted with lines, respectively: dotted, solid, and
dashed. The TAC results are marked with symbols, respectively:
down-triangles, diamonds, and up-triangles. The left and right parts
of the Figure show the TAC values of
are plotted with lines, respectively: dotted, solid, and
dashed. The TAC results are marked with symbols, respectively:
down-triangles, diamonds, and up-triangles. The left and right parts
of the Figure show the TAC values of
![]() for the planar
and chiral solutions, respectively. It is obvious that the results
obtained for the rotation about tilted axes are almost identical to
those obtained from the independent PAC calculations.
for the planar
and chiral solutions, respectively. It is obvious that the results
obtained for the rotation about tilted axes are almost identical to
those obtained from the independent PAC calculations.
Unlike the angular momentum, the average value of the total TAC Routhian,
![]() of Eq. (1), cannot be
trivially decomposed into contributions from rotations about the three
principal axes. Yet, for each TAC solution, characterized
by an angular frequency
of Eq. (1), cannot be
trivially decomposed into contributions from rotations about the three
principal axes. Yet, for each TAC solution, characterized
by an angular frequency ![]() , we have its three intrinsic
components,
, we have its three intrinsic
components, ![]() , and we can consider a sum,
, and we can consider a sum,
![]() , of the
corresponding values of the PAC Routhians,
, of the
corresponding values of the PAC Routhians,
![]() ,
i.e.,
,
i.e.,
For the chiral solution, as
![]() we take the
same value as for the planar case, because the chiral band can be
regarded as a continuation of the planar one, as discussed in
Section 3.7. The equivalent Routhian can be plotted only
in such a frequency range in which the PAC solutions are obtained for
the corresponding components
we take the
same value as for the planar case, because the chiral band can be
regarded as a continuation of the planar one, as discussed in
Section 3.7. The equivalent Routhian can be plotted only
in such a frequency range in which the PAC solutions are obtained for
the corresponding components ![]() . In that range,
. In that range,
![]() deviates from
deviates from ![]() by
not more than 30keV, as it can be seen from the Figure, whereas the
total Routhian itself drops by about 8MeV between
by
not more than 30keV, as it can be seen from the Figure, whereas the
total Routhian itself drops by about 8MeV between ![]() and
0.6MeV/
and
0.6MeV/![]() . Therefore, we conclude that the equivalent
Routhian, constructed out of the PAC solutions, reproduces the full
TAC Routhian to a very high accuracy.
. Therefore, we conclude that the equivalent
Routhian, constructed out of the PAC solutions, reproduces the full
TAC Routhian to a very high accuracy.
Another piece of information that is
contained in the TAC results, and not directly in the PAC results, is how the total
angular frequency, ![]() , should be distributed over the three
principal axes for each given point of a band representing the rotation
about a tilted axis. That, however, can also be determined from the PAC
solutions by means of the Kerman-Onishi requirement [37]
(see Section 2) that the angular-momentum vector must be
parallel to the angular-frequency vector. Indeed, this condition
is equivalent to the system of three non-linear equations,
, should be distributed over the three
principal axes for each given point of a band representing the rotation
about a tilted axis. That, however, can also be determined from the PAC
solutions by means of the Kerman-Onishi requirement [37]
(see Section 2) that the angular-momentum vector must be
parallel to the angular-frequency vector. Indeed, this condition
is equivalent to the system of three non-linear equations,
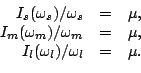 |
(28) |
We have thus demonstrated that within our HF results, the general 2D or 3D rotation separates into two or three, in a sense independent, 1D rotations about the principal axes. This is possible mainly because our solutions are very stiff against deformation changes with rotational frequency. Had they been soft, rotations about different (principal or tilted) axes could cause different shape polarizations that would prevent such a simple superposition of motions. Yet, whenever the motions are separable, the PAC calculations supplemented with the Kerman-Onishi condition are actually sufficient to describe the 2D or 3D rotations. Although this rule has to be, in principle, confirmed numerically in each particular case, it is plausible that it will hold in all analogous cases of stiff alignments, by which the difficult TAC calculations can be replaced by much more easily performed PAC calculations.