In this Appendix, we discuss elementary rotational properties of
s.p. eigenstates of a mean-field Hamiltonian, which
is symmetric with respect to the ![]() group.
The group
group.
The group ![]() comprises the time-reversal operation,
comprises the time-reversal operation, ![]() ,
three signature operations,
,
three signature operations, ![]() ,
, ![]() ,
, ![]() ,
which are rotations through 180
,
which are rotations through 180![]() about the three Cartesian
axes, and products of the time-reversal and signature operations,
which are called
about the three Cartesian
axes, and products of the time-reversal and signature operations,
which are called ![]() -signatures, cf. Ref. [45] for more
information about this group in the context of mean-field
calculations.
In most cranking solutions corresponding to quadrupole
deformation, the group
-signatures, cf. Ref. [45] for more
information about this group in the context of mean-field
calculations.
In most cranking solutions corresponding to quadrupole
deformation, the group ![]() is a symmetry group of the s.p. Hamiltonian,
is a symmetry group of the s.p. Hamiltonian, ![]() , of Eq. (3).
For a single Kramers
pair in a fixed potential, we investigate the response of the s.p. angular momenta to a cranking frequency applied in an arbitrary
direction. Our conclusions are based only on symmetry arguments, and
are thus independent on the particular implementation of the mean
field.
, of Eq. (3).
For a single Kramers
pair in a fixed potential, we investigate the response of the s.p. angular momenta to a cranking frequency applied in an arbitrary
direction. Our conclusions are based only on symmetry arguments, and
are thus independent on the particular implementation of the mean
field.
Irrespective of spatial symmetries, whenever the s.p. Hamiltonian is invariant under the time reversal, its spectrum
exhibits the two-fold Kramers degeneracy. We consider a single
Kramers pair, whose states are denoted as
![]() and
and
![]() , where
, where
| (29) |
All information about the matrix elements of the angular-momentum
operator,
![]() , between the states
, between the states
![]() and
and
![]() can be represented in a convenient way in terms of
the real alignment vector,
can be represented in a convenient way in terms of
the real alignment vector,
![]() , and the complex
decoupling vector,
, and the complex
decoupling vector,
![]() , of the state
, of the state
![]() .
They are defined as
.
They are defined as
| (30) |
| (31) |
If the s.p. Hamiltonian is symmetric with respect to the ![]() group, it is possible to chose the states forming the Kramers pair
as eigenstates of any of the three signature operators,
group, it is possible to chose the states forming the Kramers pair
as eigenstates of any of the three signature operators, ![]() , where
, where
![]() , but only one at a time, because the signature operators do
not commute among themselves, i.e., for
, but only one at a time, because the signature operators do
not commute among themselves, i.e., for ![]()
We choose states
![]() so that they correspond to eigenvalues
so that they correspond to eigenvalues ![]() under the action of
under the action of
![]() , while the eigenvalues of
, while the eigenvalues of
![]() are
are ![]() .
Multiplication rules (32) allow to easily express eigenstates
.
Multiplication rules (32) allow to easily express eigenstates
![]() ,
,
![]() ,
,
![]() , and
, and
![]() through linear combinations of eigenstates
through linear combinations of eigenstates
![]() and
and
![]() .
By fixing the relative phase
between states
.
By fixing the relative phase
between states
![]() and
and
![]() we obtain the following expressions:
we obtain the following expressions:
| (37) | |||
| (38) | |||
| (39) | |||
| (40) |
The fact that
![]() and
and
![]() are eigenstates
of
are eigenstates
of ![]() , together with the transformation rules of the
components,
, together with the transformation rules of the
components, ![]() , of the angular momentum operator under the
three signatures,
, of the angular momentum operator under the
three signatures,
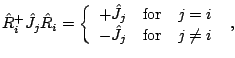 |
(41) |
From these relations and for the eigenstates defined as in Eqs. (33)-(36), it follows that all the quantities
![]() and
and
![]() can be expressed through the three
``diagonal'' components,
can be expressed through the three
``diagonal'' components,
![]() , of the alignment vector,
, of the alignment vector,
The symmetry group ![]() itself does not impose any conditions on
the``diagonal'' components,
itself does not impose any conditions on
the``diagonal'' components,
![]() . However, these
values can be further restricted if some other symmetry is present.
For example,
if
. However, these
values can be further restricted if some other symmetry is present.
For example,
if ![]() is axially symmetric, say with respect to the
is axially symmetric, say with respect to the ![]() axis,
then the states
axis,
then the states
![]() ,
,
![]() are eigenstates
of
are eigenstates
of ![]() , which leads to quantization of
, which leads to quantization of
![]() . In
fact,
. In
fact,
![]() , because
, because
![]() , while in the adopted convention
, while in the adopted convention
![]() . For states
. For states
![]() and
and
![]() , defined by (33) and (35),
one easily finds
, defined by (33) and (35),
one easily finds
| (49) |
We now consider the TAC for a single Kramers pair
in a ![]() -symmetric potential. We make two simplifying
assumptions. First, that the Hamiltonian
-symmetric potential. We make two simplifying
assumptions. First, that the Hamiltonian ![]() in the Routhian
in the Routhian
![]() of Eq. (3) does not change with rotational
frequency (non-selfconsistent cranking). Second, that the considered
Kramers pair has no coupling to other eigenstates of
of Eq. (3) does not change with rotational
frequency (non-selfconsistent cranking). Second, that the considered
Kramers pair has no coupling to other eigenstates of ![]() through the angular-momentum operator (isolated pair). The TAC under such
conditions becomes a two-dimensional diagonalization problem, that
can be solved analytically.
through the angular-momentum operator (isolated pair). The TAC under such
conditions becomes a two-dimensional diagonalization problem, that
can be solved analytically.
We use the basis of states
![]() and
and
![]() .
For a degenerate Kramers pair,
.
For a degenerate Kramers pair, ![]() reduces to its eigenvalue,
reduces to its eigenvalue,
![]() . Matrix elements of the angular-momentum operator are defined by
Eq. (46). Altogether, matrix of the s.p. Routhian
(3) takes the form
. Matrix elements of the angular-momentum operator are defined by
Eq. (46). Altogether, matrix of the s.p. Routhian
(3) takes the form
Values of alignments (53) are undefined if, and only
if, all the products
![]() vanish - in particular
when
vanish - in particular
when ![]() . In such a case, the Routhian (52) is
proportional to unity, and the mean angular momenta of its
eigenstates depend on their (arbitrary) unitary mixing.
. In such a case, the Routhian (52) is
proportional to unity, and the mean angular momenta of its
eigenstates depend on their (arbitrary) unitary mixing.
Two extreme cases of the dependence (53) deserve particular attention.
In axial nuclei, precisely one two-fold degenerate substate of each
deformation-split ![]() -shell has
-shell has
![]() and
and
![]() , which represents the soft alignment.
According to Eq. (50), all other necessarily have a
vanishing decoupling parameter, and are thus stiffly aligned with the
symmetry axis. For prolate shapes, the lowest-energy substate has
, which represents the soft alignment.
According to Eq. (50), all other necessarily have a
vanishing decoupling parameter, and are thus stiffly aligned with the
symmetry axis. For prolate shapes, the lowest-energy substate has
![]() , and is soft, while for oblate
shapes it is the highest substate. In triaxial nuclei, values of the
parameters
, and is soft, while for oblate
shapes it is the highest substate. In triaxial nuclei, values of the
parameters
![]() , where
, where ![]() corresponds to the short,
medium, and long principal axes, are equal to the s.p. alignments
obtained from the one-dimensional cranking about the three axes.
Indeed, for cranking about the axis
corresponds to the short,
medium, and long principal axes, are equal to the s.p. alignments
obtained from the one-dimensional cranking about the three axes.
Indeed, for cranking about the axis ![]() , the s.p. states are
eigenstates of
, the s.p. states are
eigenstates of ![]() . For example, from the results of
Section 3.4, one can see that for the lowest
. For example, from the results of
Section 3.4, one can see that for the lowest ![]() substates of a triaxial nucleus only
substates of a triaxial nucleus only
![]() is non-zero, while
for the highest substates only
is non-zero, while
for the highest substates only
![]() does not vanish. These
alignments are thus stiff. Note that there are no states with stiff
alignment on the medium axis. The response to rotation of the middle
does not vanish. These
alignments are thus stiff. Note that there are no states with stiff
alignment on the medium axis. The response to rotation of the middle
![]() substates is soft, because all the three
parameters,
substates is soft, because all the three
parameters,
![]() ,
,
![]() ,
,
![]() , are
non-zero.
, are
non-zero.
In realistic cranking calculations the symmetry arguments discussed
here interplay with the fact that there is angular-momentum coupling
between different Kramers pairs and that the mean field does change
with rotational frequency. In the results of the present paper,
however, the change of deformation induced by rotation is negligible.
The angular-momentum coupling of the lowest and highest ![]() substates to other s.p. states is rather weak, what can be seen from
the small curvature of their one-dimensional Routhians in
Fig. 2. The stiff character of their alignments is
fully confirmed in our self-consistent calculations, as discussed in
Section 3.4 and further in the paper. Investigation on how
suitable the notion of soft and stiff alignment is in other physical
cases remains a subject for further research.
substates to other s.p. states is rather weak, what can be seen from
the small curvature of their one-dimensional Routhians in
Fig. 2. The stiff character of their alignments is
fully confirmed in our self-consistent calculations, as discussed in
Section 3.4 and further in the paper. Investigation on how
suitable the notion of soft and stiff alignment is in other physical
cases remains a subject for further research.