To test the applicability of our method near the neutron drip line, we
performed calculations for ![]() Sn, which the Skyrme parameter set
SkM
Sn, which the Skyrme parameter set
SkM![]() with volume-type delta pairing interaction places very close
to the two-neutron drip line. The results in the isoscalar
with volume-type delta pairing interaction places very close
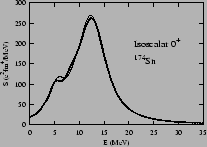
to the two-neutron drip line. The results in the isoscalar ![]() channel are shown in Fig. 1, which displays three curves
calculated within different single-particle spaces. We include
single-particle states for which occupation probabilities are larger
than a cutoff parameter
channel are shown in Fig. 1, which displays three curves
calculated within different single-particle spaces. We include
single-particle states for which occupation probabilities are larger
than a cutoff parameter
![]() (which is set to a very small
value so that we omit little of physical significance) if the system is
paired in the HFB ground state, or those for which the Hartree-Fock (HF)
energies are lower than a cutoff parameter
(which is set to a very small
value so that we omit little of physical significance) if the system is
paired in the HFB ground state, or those for which the Hartree-Fock (HF)
energies are lower than a cutoff parameter
![]() , if
the system is unpaired. In
, if
the system is unpaired. In ![]() Sn, the neutrons are paired, and
protons are unpaired in the HFB calculation. Figure 1
demonstrates that our solution converges when we make
Sn, the neutrons are paired, and
protons are unpaired in the HFB calculation. Figure 1
demonstrates that our solution converges when we make
![]() small enough and
small enough and
![]() large enough. Since the
neutrons of
large enough. Since the
neutrons of ![]() Sn are paired, there is a spurious state associated
with particle-number nonconservation. We checked that the transition
strengths for the particle-number operator are smaller than 10
Sn are paired, there is a spurious state associated
with particle-number nonconservation. We checked that the transition
strengths for the particle-number operator are smaller than 10![]() to the real excited states.
to the real excited states.
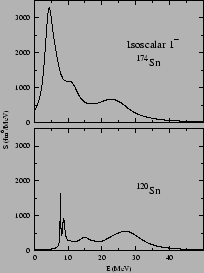
The isoscalar ![]() mode is challenging technically because of spurious
center-of-mass motion; a careful calculation is necessary to accurately
separate the spurious state from real excited states. In calculations
that are not fully self-consistent, the strength is often corrected by
including a term
mode is challenging technically because of spurious
center-of-mass motion; a careful calculation is necessary to accurately
separate the spurious state from real excited states. In calculations
that are not fully self-consistent, the strength is often corrected by
including a term
![]() (where
(where
![]() with
with
![]() the mean value in the HFB ground
state) in the isoscalar-dipole transition operator [4]. We
performed calculations of the strength functions with and without the
correction term and obtained identical results for real excited states;
our
the mean value in the HFB ground
state) in the isoscalar-dipole transition operator [4]. We
performed calculations of the strength functions with and without the
correction term and obtained identical results for real excited states;
our ![]() solutions are therefore essentially free from contamination.
In a perfect calculation, the spurious state would have zero energy and
the correction term would remove strength only from this state. In our
calculation of
solutions are therefore essentially free from contamination.
In a perfect calculation, the spurious state would have zero energy and
the correction term would remove strength only from this state. In our
calculation of ![]() Sn (
Sn (![]() Sn), even though the spurious state
energy is 0.319 (0.713) MeV, the correction removes almost no strength
except from this spurious state. This check is important for proving
that the strong enhancement of strength at low energy in nuclei near
the neutron drip line, illustrated in Fig. 2, is not an
artifact of the calculation.
Sn), even though the spurious state
energy is 0.319 (0.713) MeV, the correction removes almost no strength
except from this spurious state. This check is important for proving
that the strong enhancement of strength at low energy in nuclei near
the neutron drip line, illustrated in Fig. 2, is not an
artifact of the calculation.
Finally we mention that the energy-weighted sum rules of the ![]() ,
, ![]() , and
, and
![]() modes of
modes of ![]() Sn are satisfied with errors of
Sn are satisfied with errors of ![]() % at most.
% at most.
|
|