


Next: Results
Up: enam04mario-02w
Previous: Introduction
Particle-Number-Projected Skyrme-HFB Method
The particle-number-projected HFB state can be written as:
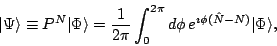 |
(1) |
where 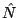 is the number operator,
is the number operator, 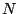 is the particle number,
and
is the particle number,
and 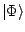 is the HFB wavefunction which does not have a
well-defined particle number. As shown in Ref. [3], the PNP
HFB energy
is the HFB wavefunction which does not have a
well-defined particle number. As shown in Ref. [3], the PNP
HFB energy
![\begin{displaymath}
\textsf{E}^{N}[\rho,\bar{\rho}]=\frac{\left\langle \Phi \ver...
...langle \Phi \vert e^{i\phi ({\hat{N}}-N)}\vert\Phi
\rangle },
\end{displaymath}](img15.png) |
(2) |
is an energy functional of the unprojected particle-hole
and pairing densities 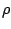 and
and 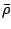 , respectively.
In the case of the Skyrme force, the projected energy (2)
reads:
, respectively.
In the case of the Skyrme force, the projected energy (2)
reads:
![\begin{displaymath}
\textsf{E}^{N}[\rho,\tilde{\rho}]= \int d\phi ~y(\phi ) \int...
...f
r} \left({ H}({\bf r},\phi)+\tilde{ H}({\bf
r},\phi)\right),
\end{displaymath}](img18.png) |
(3) |
where
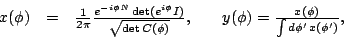 |
(4) |
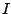 is the unit matrix, and the gauge-angle-dependent energy
densities
is the unit matrix, and the gauge-angle-dependent energy
densities
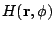 and
and
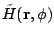 are
derived from the unprojected ones by simply replacing particle
(pairing) local densities by their gauge-angle-dependent
counterparts. The latter ones are defined by the
gauge-angle-dependent density matrices.
are
derived from the unprojected ones by simply replacing particle
(pairing) local densities by their gauge-angle-dependent
counterparts. The latter ones are defined by the
gauge-angle-dependent density matrices.
Obviously, the projected energy (3) is a functional
of the unprojected density matrices. Its
derivatives with respect to
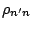 and
and
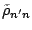 lead to the PNP Skyrme-HFB equations
lead to the PNP Skyrme-HFB equations
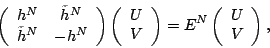 |
(5) |
where
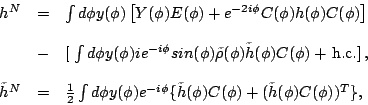 |
(6) |
and
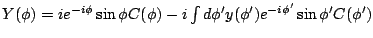 and
and
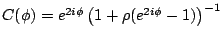 . The gauge-angle-dependent field
matrices
. The gauge-angle-dependent field
matrices 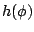 and
and
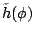 are obtained by simply
replacing the particle and pairing local densities in the
unprojected fields with their gauge-angle-dependent counterparts.
are obtained by simply
replacing the particle and pairing local densities in the
unprojected fields with their gauge-angle-dependent counterparts.



Next: Results
Up: enam04mario-02w
Previous: Introduction
Jacek Dobaczewski
2005-01-24
![]() and
and
![]() lead to the PNP Skyrme-HFB equations
lead to the PNP Skyrme-HFB equations