


Next: Results
Up: enam04piotr-07w
Previous: Introduction
By using the code HFBTHO [3], we perform the HFB calculations
within the particle space of 20 harmonic oscillator shells, which
leads to the single-particle energies of 200MeV and above. When
no truncation is performed in the quasiparticle space, the Bogoliubov
transformation is unitary, and this guarantees that the pairing
tensor 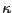 is antisymmetric. This is no longer
true for the finite energy cutoff.
The inset in Fig. 1 shows
the maximum matrix element of the symmetric and antisymmetric parts
of the pairing tensor as functions of the cutoff energy
is antisymmetric. This is no longer
true for the finite energy cutoff.
The inset in Fig. 1 shows
the maximum matrix element of the symmetric and antisymmetric parts
of the pairing tensor as functions of the cutoff energy 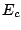 in the
quasiparticle space. Typically, the former does not exceed 1% of the
latter; however, a non-zero symmetric component means that the fermion
quasiparticle state representing the HFB ground state does not exist.
Usually one simply disregards this symmetric part in the Skyrme-HFB
calculations.
in the
quasiparticle space. Typically, the former does not exceed 1% of the
latter; however, a non-zero symmetric component means that the fermion
quasiparticle state representing the HFB ground state does not exist.
Usually one simply disregards this symmetric part in the Skyrme-HFB
calculations.
Figure 1:
Total energies of 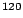 Sn obtained for the Sly4 Skyrme
functional and different values of the energy and SVD cutoffs. Stars
correspond to the standard HFB solutions and diamonds to two values
of the SVD cutoff:
Sn obtained for the Sly4 Skyrme
functional and different values of the energy and SVD cutoffs. Stars
correspond to the standard HFB solutions and diamonds to two values
of the SVD cutoff: 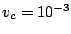 and
and 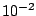 . The maximum
matrix element of the antisymmetric (left scale) and symmetric
(right scale) parts of the pairing tensor are shown in the inset.
. The maximum
matrix element of the antisymmetric (left scale) and symmetric
(right scale) parts of the pairing tensor are shown in the inset.
|
|
Our method ensures the antisymmetricity of the pairing
tensor and, at the same time, keeps the number of quasiparticle states
limited. The approach is based on finding an optimal truncated
particle space, dictated by a given quasiparticle truncation, in
which the HFB equations are solved without any further cutoff.
Full-space diagonalization of the HFB equations is necessary only to
provide the aforementioned optimal basis.
The Singular Value Decomposition (SVD) [4] is an algebraic method, which, by
means of finding the so-called singular values, orders orthonormal
basis states according to their importance for decomposition of a
rectangular matrix into a sum of components. We use it to decompose
the combined matrix ![$[B^*A^*]$](img17.png) , where
, where 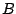 and
and 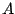 are the Bogoliubov
matrices corresponding to a non-unitary transformation, and assemble
the optimal basis by taking only those particle states which have the
corresponding singular values above a certain SVD cutoff,
are the Bogoliubov
matrices corresponding to a non-unitary transformation, and assemble
the optimal basis by taking only those particle states which have the
corresponding singular values above a certain SVD cutoff, 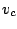 .
Since for each value of the SVD cutoff the dimension of the resulting
particle space is different, one has to refit the pairing strength
as function of
.
Since for each value of the SVD cutoff the dimension of the resulting
particle space is different, one has to refit the pairing strength
as function of 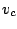 . We do it so that the pairing gap is the same in
both steps: in the full-space solution obtained for a given energy
cutoff and in the truncated-space solution. Our
calculations are carried out according to the following scheme:
. We do it so that the pairing gap is the same in
both steps: in the full-space solution obtained for a given energy
cutoff and in the truncated-space solution. Our
calculations are carried out according to the following scheme:
- Self-consistent solution of the HFB equations in the full space.
- Singular Value Decomposition of the combined matrix
![$[B^*A^*]$](img17.png) corresponding to the full-space solution.
corresponding to the full-space solution.
- Defining the truncated particle space by keeping the SVD states that
correspond to singular values above the SVD cutoff
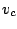 .
.
- Self-consistent solution of the HFB equations in the truncated
particle space.
- Fitting the pairing strength by repeating step
(d) with different pairing strengths until the
pairing gaps in the full and truncated spaces are equal.
Figure 2:
Number of neutron particle states in
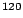 Sn in the
truncated spaces (solid lines) and numbers of quasiparticle states
below the cutoff energies (dotted lines) as functions of the SVD
cutoff, for different values of the
energy cutoff.
Sn in the
truncated spaces (solid lines) and numbers of quasiparticle states
below the cutoff energies (dotted lines) as functions of the SVD
cutoff, for different values of the
energy cutoff.
|
|



Next: Results
Up: enam04piotr-07w
Previous: Introduction
Jacek Dobaczewski
2005-01-23
![\includegraphics[width=0.95\columnwidth]{gap_truncated_mixed_full_total_no_states_col.eps}](img16.png)
![\includegraphics[width=0.95\columnwidth]{gap_truncated_mixed_full_total_no_states_col.eps}](img16.png)
![]() , where
, where ![]() and
and ![]() are the Bogoliubov
matrices corresponding to a non-unitary transformation, and assemble
the optimal basis by taking only those particle states which have the
corresponding singular values above a certain SVD cutoff,
are the Bogoliubov
matrices corresponding to a non-unitary transformation, and assemble
the optimal basis by taking only those particle states which have the
corresponding singular values above a certain SVD cutoff, ![]() .
Since for each value of the SVD cutoff the dimension of the resulting
particle space is different, one has to refit the pairing strength
as function of
.
Since for each value of the SVD cutoff the dimension of the resulting
particle space is different, one has to refit the pairing strength
as function of ![]() . We do it so that the pairing gap is the same in
both steps: in the full-space solution obtained for a given energy
cutoff and in the truncated-space solution. Our
calculations are carried out according to the following scheme:
. We do it so that the pairing gap is the same in
both steps: in the full-space solution obtained for a given energy
cutoff and in the truncated-space solution. Our
calculations are carried out according to the following scheme:
![\includegraphics[width=0.95\columnwidth]{gap_truncated_volume_full_no_states_svd_col.eps}](img21.png)