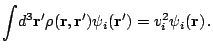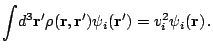Canonical basis

The canonical states are obtained by diagonalizing the density matrix (see e.g. Refs. [10,18] for the interpretation of the canonical basis)

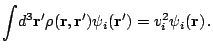$$\int\!d^3\mathbf r'\rho({\mathbf r},{\mathbf r}')\psi_i({\mathbf r}')=v_i^2\psi_i({\mathbf r})\,.$$ (50)

As discussed in Refs. [5,18], all canonical states have localized wave functions and form a basis. The energies of the canonical states are defined as the diagonal matrix elements of the Hartree-Fock field 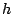$h$ in the canonical basis,

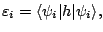$$\varepsilon_i=\langle\psi_i\vert h\vert\psi_i\rangle ,$$ (51)

and the pairing gaps associated with these states are the diagonal matrix elements of the pairing field,

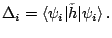$$\Delta_i=\langle\psi_i\vert\tilde h\vert\psi_i\rangle\,.$$ (52)

Finally, the canonical quasiparticle energy can be defined using the same kind of formula as (48),

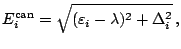$$E^{\text{can}}_i=\sqrt{(\varepsilon_i-\lambda)^2+\Delta_i^2}\,,$$ (53)

while the occupation probabilities of canonical states are given by

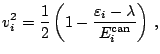$$v_i^2=\frac{1}{2}\left(1-\frac{\varepsilon_i-\lambda}{E^{\text{can}}_i}\right)\,,$$ (54)

These characteristics of the canonical states can be found in the output file hfb_n_p.spe, see Sec. 7.