


Next: Local gauge transformations of
Up: Galilean and gauge invariance
Previous: Galilean and gauge invariance
The gauge-transformed nonlocal densities read [25,36,24]
Since the local gauge transformations form a U(1) group, invariance
with respect to transformations that are of the first-order in gauge
angles,
![$ \left[1+iG\right]\rho(\vec {r},\vec {r}')$](img494.png) , where
, where
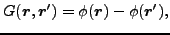 |
(36) |
is enough to ensure full gauge invariance. By Taylor expanding
the exponential functions in eq. 34 and 35
after they are inserted in the functional one may, of course,
also prove this fact explicitly.
One specific type of gauge transformation is the Galilean
transformation, for which the gauge angles depend linearly on
positions, i.e.,
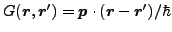 , and which
corresponds to a transformation to a reference frame that moves
with velocity
, and which
corresponds to a transformation to a reference frame that moves
with velocity
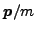 . For this transformation, only first-order
derivatives of
. For this transformation, only first-order
derivatives of 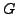 survive, which makes Galilean invariance
less restrictive than the full gauge invariance.
survive, which makes Galilean invariance
less restrictive than the full gauge invariance.



Next: Local gauge transformations of
Up: Galilean and gauge invariance
Previous: Galilean and gauge invariance
Jacek Dobaczewski
2008-10-06
![]() , and which
corresponds to a transformation to a reference frame that moves
with velocity
, and which
corresponds to a transformation to a reference frame that moves
with velocity
![]() . For this transformation, only first-order
derivatives of
. For this transformation, only first-order
derivatives of ![]() survive, which makes Galilean invariance
less restrictive than the full gauge invariance.
survive, which makes Galilean invariance
less restrictive than the full gauge invariance.