


Next: Potentials in the spherical
Up: The NLO potentials, fields,
Previous: Spherical HO basis
Densities in the spherical HO basis
For any density matrix one can always
perform a multipole expansion.
This strategy fits very well our applications
to the spherical HF solutions, where only the monopole component of
the density matrix is nonzero, and to the RPA applications in spherical
nuclei, where all multipole excitations separate from one another. Therefore,
in what follows we consider the density matrix of multipolarity 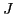 in the form given by the Wigner-Eckart theorem:
in the form given by the Wigner-Eckart theorem:
and depending on its reduced matrix elements
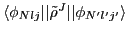 Then, the non-local densities can be expressed in terms of the
spherical HO wave functions (79) as
Then, the non-local densities can be expressed in terms of the
spherical HO wave functions (79) as
that is,
We can now replace the spin coordinates by the spin projections,
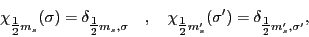 |
(90) |
and we can use the Wigner-Eckart theorem for the Pauli matrices,
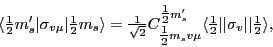 |
(91) |
with
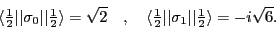 |
(92) |
After inserting the nonlocal density (93) into
the expression for local densities (76), and after acting
with derivatives on spherical wave functions, as in Eqs. (81) and (82),
we obtain
where, by using the phase convention
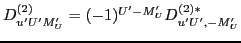 ,
we have introduced the complex conjugation into the derivative
operator (31).
,
we have introduced the complex conjugation into the derivative
operator (31).
After a lengthy but straightforward derivation presented
in B, we obtain the following result:
for the radial form factors
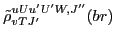 given by:
given by:
where
In view of the fact that only the coefficients
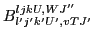 for
for
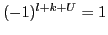 and
and
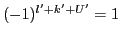 are required in Eq. (99),
we may replace them by coefficients
are required in Eq. (99),
we may replace them by coefficients
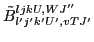 :
:
where we have used symmetry properties of 9j symbols under the
transposition of rows and columns and transposition with respect to
the main diagonal.
Finally, all secondary densities of Eq. (77) can
now be calculated in terms of one compact expression:
where the radial form factors read



Next: Potentials in the spherical
Up: The NLO potentials, fields,
Previous: Spherical HO basis
Jacek Dobaczewski
2010-01-30
![]() in the form given by the Wigner-Eckart theorem:
in the form given by the Wigner-Eckart theorem: