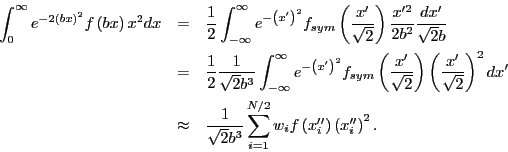Next: Overview of the software
Up: The NLO potentials, fields,
Previous: Exchange Coulomb energy
Numerical integration
Numerical Gauss-Hermite integration is used to calculate the radial integrals occurring in the expressions for
matrix elements [Eqs. (113) and (114)] and total energies [Eq. (120)]. This kind of integration
is for integrals of the form
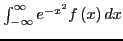 , and in order to
obtain this form our integrals are transformed by using
, and in order to
obtain this form our integrals are transformed by using
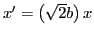 . The integrals
can then be written as:
. The integrals
can then be written as:
Where
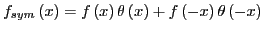 was used in an intermediate step.
To reduce the number of grid points by half to
was used in an intermediate step.
To reduce the number of grid points by half to
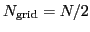 it was also used that for Gauss-Hermite integration, the weight functions
it was also used that for Gauss-Hermite integration, the weight functions 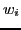 and
grid points
and
grid points
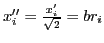 are symmetric about the origin. The integrals for matrix elements and total energies
of most terms become exact when
are symmetric about the origin. The integrals for matrix elements and total energies
of most terms become exact when
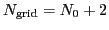 , where
, where 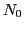 denotes the maximum HO shell included in the basis.
But in general more points are needed when the integrand cannot be expressed
as a product of four basis states, e.g., in the
case for the Coulomb interaction and also for the density-dependent terms.
denotes the maximum HO shell included in the basis.
But in general more points are needed when the integrand cannot be expressed
as a product of four basis states, e.g., in the
case for the Coulomb interaction and also for the density-dependent terms.
Jacek Dobaczewski
2010-01-30
![]() , and in order to
obtain this form our integrals are transformed by using
, and in order to
obtain this form our integrals are transformed by using
![]() . The integrals
can then be written as:
. The integrals
can then be written as: