


Next: Bibliography
Up: Solution of self-consistent equations
Previous: Derivation of Eq. (98)
Derivation of Eq. (113)
After inserting Eq. (111) into Eq. (112)
we must sum up products of four Clebsh-Gordan coefficients, similarly as in Eq. (129),
that is,
and then as in Eq. (131):
We can now perform the summation over 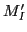 and
and 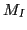 , which gives the factor
, which gives the factor
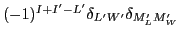 and allows for a summation over
and allows for a summation over 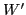 and
and 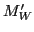 . After inserting all these results into
Eq. (112), we obtain
. After inserting all these results into
Eq. (112), we obtain
Now, we have to sum up products of three Clebsh-Gordan coefficients,
similarly as in Eq. (133), that is,
This gives:
Finally, summations over 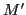 and
and 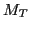 give the factor
give the factor
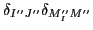 ,
that is:
,
that is:
where we have also used Eq. (90).
This shows explicitly that in the field calculated for the density
matrix with multipolarity 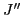 , only the multipole
, only the multipole 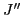 appears.
appears.
References



Next: Bibliography
Up: Solution of self-consistent equations
Previous: Derivation of Eq. (98)
Jacek Dobaczewski
2010-01-30
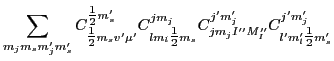
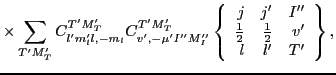
![]() and
and ![]() , which gives the factor
, which gives the factor
![]() and allows for a summation over
and allows for a summation over ![]() and
and ![]() . After inserting all these results into
Eq. (112), we obtain
. After inserting all these results into
Eq. (112), we obtain