


Next: Regularization of the Contact
Up: Large-Scale Microscopic Nuclear Mass
Previous: Large-Scale Microscopic Nuclear Mass
Going away from the beta stability valley
towards particle drip lines, the
Fermi energy becomes very small and the nucleonic densities and fields
acquire large spatial extensions due to the coupling to the particle
continuum. In this region of weakly bound nuclei, the asymptotic
behavior of nuclear densities has an effect on nuclear properties.
Consequently, when performing calculations for drip-line systems,
it is important
to have a firm grasp on physics at large distances.
The recently developed HFB-THO technique
based on the transformed harmonic oscillator (THO) method
[27,28,22] is very helpful in this respect:
it is fast, efficient, and easy to implement.
Figure 3:
Comparison of the neutron densities
(in logarithmic scale) calculated for the deformed nucleus
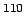 Zn using coordinate-space 2D calculations
(solid squares) with the configurational calculations based on
THO (open squares) and HO (open circles) basis [29].
Each point corresponds to
one Gauss-integration node in the
Zn using coordinate-space 2D calculations
(solid squares) with the configurational calculations based on
THO (open squares) and HO (open circles) basis [29].
Each point corresponds to
one Gauss-integration node in the 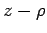 plane, and the results
are plotted as functions of the distance from the origin,
plane, and the results
are plotted as functions of the distance from the origin,
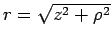 .
.
![\includegraphics[width=0.9\textwidth]{fig3.eps}](img69.png) |
Figure 3 shows the neutron density
of the deformed nucleus
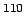 Zn obtained
in two
configurational calculations based on expansions in the harmonic
oscillator (HO) and THO bases
[27,28,22] compared to full-fledged
2D coordinate-space calculations [30,29] with the box
boundary conditions.
Every point in the figure
corresponds to the value of the neutron density at a given
Gauss-integration node in the
Zn obtained
in two
configurational calculations based on expansions in the harmonic
oscillator (HO) and THO bases
[27,28,22] compared to full-fledged
2D coordinate-space calculations [30,29] with the box
boundary conditions.
Every point in the figure
corresponds to the value of the neutron density at a given
Gauss-integration node in the 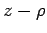 plane. Since the nucleus is
deformed, and there are always several nodes near a sphere of the
same radius
plane. Since the nucleus is
deformed, and there are always several nodes near a sphere of the
same radius
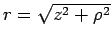 , there can be seen some
scatter of points corresponding to different densities in different
directions.
While the significant deviation from the correct
decaying behavior is seen in the HO results, the THO expansion
agrees very well with the deformed coordinate-space method.
Other promising techniques that can alternatively be used in this
context are the
Gaussian-expansion basis method [31] and the Berggren
expansion method [32].
, there can be seen some
scatter of points corresponding to different densities in different
directions.
While the significant deviation from the correct
decaying behavior is seen in the HO results, the THO expansion
agrees very well with the deformed coordinate-space method.
Other promising techniques that can alternatively be used in this
context are the
Gaussian-expansion basis method [31] and the Berggren
expansion method [32].



Next: Regularization of the Contact
Up: Large-Scale Microscopic Nuclear Mass
Previous: Large-Scale Microscopic Nuclear Mass
Jacek Dobaczewski
2006-01-17
![\includegraphics[width=0.9\textwidth]{fig3.eps}](img69.png)
![\includegraphics[width=0.9\textwidth]{fig3.eps}](img69.png)