

Next: Results
Up: Giant Monopole Resonances and
Previous: Separable Pairing Interaction
Nuclear Incompressibility
The isoscalar incompressibility of infinite nuclear matter is defined by
the well-known formula [1]
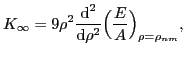 |
(29) |
where  is the saturation density of nuclear matter. Of
course,
is the saturation density of nuclear matter. Of
course,
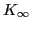 cannot be directly measured; however, by using
Eq. (29) it can be calculated from theoretical equation of
state
cannot be directly measured; however, by using
Eq. (29) it can be calculated from theoretical equation of
state 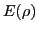 or it can be indirectly estimated from measurements
of monopole excitations of finite nuclei.
or it can be indirectly estimated from measurements
of monopole excitations of finite nuclei.
The incompressibility of finite nucleus, 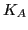 , is defined by its scaling-model
relation [28] to
the centroid of the giant monopole resonance (GMR),
, is defined by its scaling-model
relation [28] to
the centroid of the giant monopole resonance (GMR),
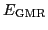 , as
, as
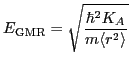 |
(30) |
where
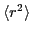 is the average square radius of the nucleus.
Eq. (30) is derived under the assumption that most of the monopole
strength is concentrated within one dominant peak, see Ref. [1].
The centroid of the GMR can be extracted from its strength function as
the ratio of the first and zero moments, that is,
is the average square radius of the nucleus.
Eq. (30) is derived under the assumption that most of the monopole
strength is concentrated within one dominant peak, see Ref. [1].
The centroid of the GMR can be extracted from its strength function as
the ratio of the first and zero moments, that is,
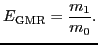 |
(31) |
There exist several alternative ways to extract
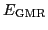 through
different moments of the strength function, such as
through
different moments of the strength function, such as
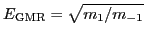 or
or
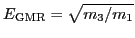 . However, they are more sensitive
to details of the strength function and thus less appropriate
for studies of the incompressibility.
. However, they are more sensitive
to details of the strength function and thus less appropriate
for studies of the incompressibility.
In analogy to the Weizsäcker formula for the nuclear masses,
one can introduce [1] a similar relation for nuclear incompressibilities,
Similarly as in the liquid-drop model, we refer to 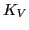 ,
, 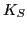 ,
, 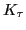 ,
,
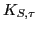 , and
, and 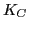 as the volume, surface, symmetry, surface-symmetry,
and Coulomb incompressibility parameters, respectively. By adjusting
these parameters to the incompressibilities
as the volume, surface, symmetry, surface-symmetry,
and Coulomb incompressibility parameters, respectively. By adjusting
these parameters to the incompressibilities 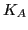 , calculated in finite nuclei
from Eqs. (30) and (31),
we can obtain an estimate of the infinite-matter incompressibility as
, calculated in finite nuclei
from Eqs. (30) and (31),
we can obtain an estimate of the infinite-matter incompressibility as
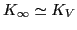 .
.


Next: Results
Up: Giant Monopole Resonances and
Previous: Separable Pairing Interaction
Jacek Dobaczewski
2012-02-28
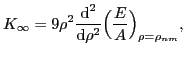
![]() , is defined by its scaling-model
relation [28] to
the centroid of the giant monopole resonance (GMR),
, is defined by its scaling-model
relation [28] to
the centroid of the giant monopole resonance (GMR),
![]() , as
, as