

Next: Spherical symmetry
Up: SPATIAL SYMMETRIES OF THE
Previous: Introduction
Density matrices and densities
Within the HFB approach to the nuclear many-body problem, the mean
value of a many-body Hamiltonian is a functional (the energy
functional) of the p-h and p-p density matrices defined,
respectively, as
where
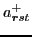 and
and
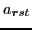 create and
annihilate, respectively, nucleons at point
create and
annihilate, respectively, nucleons at point 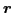 , spin
, spin
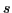 =
=
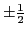 , and isospin
, and isospin 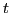 =
=
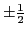 , while
, while
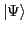 is the HFB independent-quasiparticle state. The properties of density matrices that
directly result from their definitions are the following:
is the HFB independent-quasiparticle state. The properties of density matrices that
directly result from their definitions are the following:
The dependence on the spin and isospin variables in the density
matrices can be easily separated by expanding in the spin and isospin
Pauli matrices
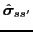 and
and
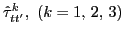 , respectively:
, respectively:
where
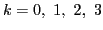 .
The spin-isospin components of the p-h (
.
The spin-isospin components of the p-h (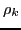 ,
, 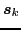 ) and
p-p
(
) and
p-p
(
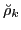 ,
,
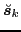 )
nonlocal densities are functions of two position vectors
)
nonlocal densities are functions of two position vectors 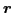 and
and
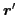 and have the following symmetry properties that result from
Eqs. (3) and (4):
and have the following symmetry properties that result from
Eqs. (3) and (4):
for 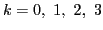 , and:
, and:
where the upper sign is for 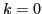 (isoscalars) and the lower for
(isoscalars) and the lower for 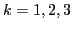 (isovectors).
(isovectors).
In general, the p-h and p-p density matrices transform differently
under the single-particle unitary transformations.
However, it is proved in I that for the spatial transformations such as
rotations, space-inversion, etc., the transformation rules for the
p-p density matrix are the same as those for the p-h density matrix.
These rules are obviously the same for all the isospin components.
Therefore, in further discussion of the space symmetries, we shall
omit the accent ``breve" and the index 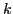 . Also, we shall not take
into account conditions (7) and (8), i.e., the
hermiticity of the p-h densities and the symmetry or antisymmetry
of the p-p densities. We mention only that the former condition
ensures the reality of all the p-h local densities, whereas the latter
one results in vanishing of either the isoscalar or the isovector p-p
local densities.
. Also, we shall not take
into account conditions (7) and (8), i.e., the
hermiticity of the p-h densities and the symmetry or antisymmetry
of the p-p densities. We mention only that the former condition
ensures the reality of all the p-h local densities, whereas the latter
one results in vanishing of either the isoscalar or the isovector p-p
local densities.
Within the local
density approximation, the
energy functional is built from
the local densities (
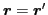 ) and derivatives thereof.
The exact definitions of all used local
densities are given, e.g., in Refs.[9,10]. Here we only provide
schematic definitions that clearly expose the corresponding spatial properties.
The densities of interest are:
) and derivatives thereof.
The exact definitions of all used local
densities are given, e.g., in Refs.[9,10]. Here we only provide
schematic definitions that clearly expose the corresponding spatial properties.
The densities of interest are:
- zero-order local densities
- particle or pairing density
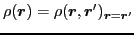 |
(9) |
- spin density
 |
(10) |
- first-order local densities
- second-order local densities
- kinetic density
![$\displaystyle {\tau}(\bm{r}) =\big[ (\bm{\nabla}\cdot\bm{\nabla}') {\rho}(\bm{r},\bm{r}')\big]_{\bm{r}=\bm{r}'}$](img58.png) |
(16) |
- spin-kinetic density
![$\displaystyle \bm{T}(\bm{r}) =\big[ (\bm{\nabla}\cdot\bm{\nabla}') \bm{s}(\bm{r},\bm{r}')\big]_{\bm{r}=\bm{r}'}$](img59.png) |
(17) |
- spin-tensor density
![$\displaystyle {\bm{F}}(\bm{r}) =\tfrac{1}{2}\big[ (\bm{\nabla} \!\otimes\!\bm{\...
...!\otimes\!\bm{\nabla})\!\cdot\! {\bm{s}}(\bm{r},\bm{r}')\big]_{\bm{r}=\bm{r}'}.$](img60.png) |
(18) |
We confine ourselves to the second-order derivatives as is usually
done. But our analysis can also be extended to higher-order derivatives
of the nonlocal densities that
have recently been considered.[11]

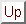

Next: Spherical symmetry
Up: SPATIAL SYMMETRIES OF THE
Previous: Introduction
Jacek Dobaczewski
2010-01-30
![]() . Also, we shall not take
into account conditions (7) and (8), i.e., the
hermiticity of the p-h densities and the symmetry or antisymmetry
of the p-p densities. We mention only that the former condition
ensures the reality of all the p-h local densities, whereas the latter
one results in vanishing of either the isoscalar or the isovector p-p
local densities.
. Also, we shall not take
into account conditions (7) and (8), i.e., the
hermiticity of the p-h densities and the symmetry or antisymmetry
of the p-p densities. We mention only that the former condition
ensures the reality of all the p-h local densities, whereas the latter
one results in vanishing of either the isoscalar or the isovector p-p
local densities.
![]() ) and derivatives thereof.
The exact definitions of all used local
densities are given, e.g., in Refs.[9,10]. Here we only provide
schematic definitions that clearly expose the corresponding spatial properties.
The densities of interest are:
) and derivatives thereof.
The exact definitions of all used local
densities are given, e.g., in Refs.[9,10]. Here we only provide
schematic definitions that clearly expose the corresponding spatial properties.
The densities of interest are: