Angular-momentum projection near the band termination

In the vicinity of band termination, the number of contributing configurations drops down and the physics simplifies significantly. Reliable approximate analytical symmetry restoration schemes can be easily derived for these cases; for details we refer the reader to the analysis presented recently in Refs. [28,29]. In the present paper we aim at further studying and testing these approximate methods against rigorous AMP results.

Let us first consider the energy splittings between the favored- and unfavored-signature terminating states, $[f_{7/2}^n]_{I_{\text{max}}}$ and $[f_{7/2}^n]_{I_{\text{max}}-1}$, respectively, within the $[f_{7/2}^n]$ configurations, where $n$ denotes the number of particles in the $f_{7/2}$ sub-shell. Within the naïve noncollective cranking model, the unique aligned $\vert\Phi_{I_{\text{max}}}\rangle$ states can be considered as many-body reference states (HF vacua) with projections of the angular momentum being conserved quantum numbers equal to the maximum allowed values, $I_y=I_{\text{max}}$. From these local HF vacua, the $\vert\Phi_{I_{\text{max}}-1}^{(\tau)}\rangle$ states can be generated by particle-hole (ph) excitations; in particular, by changing either the signature of a single neutron ($\tau=\nu$) or a single proton ($\tau=\pi$). In spite of the fact that the underlying CHF solutions are almost spherical, they manifestly break the rotational invariance. Indeed, the two $I_{\text{max}}\!-\!1$ CHF solutions have conserved projections of the angular momentum, $I_y=I_{\text{max}}\!-\!1$, but are in this case linear combinations of the total-angular momentum states with $I=I_{\text{max}}$ and $I_{\text{max}}\!-\!1$, i.e., up to a normalization factor:

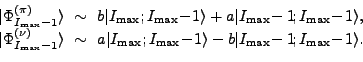$$\begin{array}{rcl} \vert\Phi_{I_{\text{max}}-1}^{(\pi)}\rangl... ..._{\text{max}}\!-1\!;I_{\text{max}} \!-\!1 \rangle . \end{array}$$ (14)

The simplicity of the encountered situation allows for an approximate analytical estimate of mixing coefficients $a$ and $b$ [28,29]. Equivalently, one can find these coefficients by performing the exact AMP of the $\vert\Phi_{I_{\text{max}}-1}^{(\pi)}\rangle$ or $\vert\Phi_{I_{\text{max}}-1}^{(\pi)}\rangle$ states. The resulting probabilities $P(I_{\text{max}}-1)$ of finding the $I_{\text{max}}\!-\!1$ components within the $\vert\Phi^{(\pi)}_{I_{\text{max}}-1}\rangle$ states are shown in Fig. 5a. The AMP results match perfectly the analytical results obtained in Refs. [28,29], confirming reliability of the approximate method.

Calculated energy differences $E(I_{\text{max}})-E(I_{\text{max}}\!-\!1)$ are shown in Fig. 5b. Since the CHF solutions break the isobaric invariance, the AMPs of the $\vert\Phi_{I_{\text{max}}-1}^{(\pi)}\rangle$ and $\vert\Phi_{I_{\text{max}}-1}^{(\nu)}\rangle$ states are not fully equivalent, and lead to slightly different energies. Results shown in Fig. 5 represent arithmetic averages of both AMP energies. The only exception is $^{42}$Sc, where we were able to perform numerical integration with a desired accuracy only when projecting from the $\vert\Phi_{I_{\text{max}}-1}^{(\nu)}\rangle$ CHF state, and the depicted point represents this single result. It is evident from the Figure that, except for $^{42}$Sc and $^{45}$Sc, the quality of the results is comparable to the state-of-the-art shell-model calculations of Refs. [30,29].

Figure: Upper panel (a): probabilities of finding the $I_{\text{max}}\!-\!1$ spin components in the $\vert\Phi^{(\pi)}_{I_{\text{max}}-1}\rangle$ CHF solutions. Squares and dots show results calculated using the exact AMP and approximate method of Ref. [28], respectively. Lower panel (b): energy differences between the favored- and unfavored-signature terminating states, $[f_{7/2}^n]_{I_{\text{max}}}$ and $[f_{7/2}^n]_{I_{\text{max}}-1}$, respectively. Values calculated using the AMP method (diamonds) are compared to those obtained within the shell-model [28] (circles) and empirical data [31,32,33,34,35,36] (dots).

The unfavored-signature $I_{\text{max}}\!-\!1$ CHF states discussed above were created by building the signature-inverting ph excitations on top of the $I_{\text{max}}$ reference state. Similar procedure applied to create $I_{\text{max}}\!-\!2$ CHF solutions leads to several nearly-spherical states, located, on average, above the reference state.

In this case, however, the SSB mechanism enters the game by pushing the collective (deformed) CHF solution down, below the reference state, and relatively close to the empirical energy. Hence, by going from the $I_{\text{max}}\!-\!1$ to $I_{\text{max}}\!-\!2$ states, the physics changes quite dramatically, showing clearly two contrasting facets of the SSB mechanism of rotational symmetry in nuclear physics.

Figure 6: Energy differences between the $[f_{7/2}^n]_{I_{\text{max}}}$ terminating states and the lowest $[f_{7/2}^n]_{I_{\text{max}}-2}$ states. Dots and circles represent the empirical data [31,32,33,34,35,36,37] and SM results of Ref. [28], respectively. Open diamonds label the lowest CHF solutions, which are collective except for the cases of $^{42}$Ca and $^{42,43}$Sc. Full diamonds represent the AMP results. Relative energies between the $I_{\text{max}}$ reference state, non-collective ph $I_{\text{max}}\!-\!1$ and $I_{\text{max}}\!-\!2$ excitations (thin lines), SSB effect in the $I_{\text{max}}\!-\!2$ state (thick dashed line), and final AMP configuration mixing (solid lines) are schematically illustrated in the inset.

In the case of the $I_{\text{max}}\!-\!1$ states, the symmetry restoration results in a repulsion of two nearly-degenerate proton and neutron CHF states, which are located above the reference $I_{\text{max}}$ state. On the one hand, the reorientation mode, $\vert I_{\text{max}};I_{\text{max}}\!-\!1\rangle$, is shifted down and becomes degenerate with the $\vert I_{\text{max}};I_{\text{max}}\rangle$ solution, as required by the rotational invariance. On the other hand, the physical mode, $\vert I_{\text{max}}\!-\!1;I_{\text{max}}\!-\!1\rangle$, is shifted up and becomes the unfavored-signature terminating state.

In the case of the $I_{\text{max}}\!-\!2$ states, the SSB mechanism results in a repulsion of several nearly-degenerate proton and neutron ph states. The collective CHF mode, $\vert\Phi_{I_{\text{max}}-2}\rangle$, is shifted below the reference $I_{\text{max}}$ state, in accordance with data. By the AMP mixing, the symmetry-restored collective mode projected from $\vert\Phi_{I_{\text{max}}-2}\rangle$, i.e., the $\vert I_{\text{max}}\!-\!2;I_{\text{max}}\!-\!2\rangle$ state, gains some additional binding energy. The situation described above is schematically illustrated in the inset of Fig. 6.

Calculated energy differences, $E(I_{\text{max}})-E(I_{\text{max}}\!-\!2)$, are shown in Fig. 6. The CHF solutions, except for $^{42}$Ca and $^{42,43}$Sc, correspond to collective states having $\beta_2\sim$ 0.10 - 0.12. The AMP shifts these states almost uniformly down by about 300 - 400keV, enlarging the splitting by that amount, and improving an overall agreement between theory and experiment. It is, however, evident from the Figure that, here, the AMP does not improve upon the incorrect isotopic/isotonic dependence of the CHF results. The magnitude of rotational correction is determined predominantly by the shape change, and does not vary from case to case. One can speculate that a detailed agreement with data would require an additional isospin-symmetry restoration.

Figure 7: Energy differences between the $[d_{3/2}^{-1}f_{7/2}^{n+1}]_{I_{\text{max}}}$ terminating states and the lowest $[d_{3/2}^{-1}f_{7/2}^{n+1}]_{I_{\text{max}}\!-\!2}$ states. Dots and circles represent empirical data [31,32,33,34,35,36,37] and SM results of Ref. [28], respectively. Open and full diamonds label the collective CHF solutions and AMP results, respectively.

A similar trend was found for the $I_{\text{max}}\!-\!2$ states for configurations involving one-proton ph excitation from $d_{3/2}$ to $f_{7/2}$ subshell, see Fig. 7. Here, all the lowest $I_{\text{max}}\!-\!2$ states are found to be deformed. The energy gain due to the AMP is again of the order of 300 - 400keV and weakly depends on $N$ and $Z$, thus merely reflecting an increase of deformation between nearly-spherical $I_{\text{max}}$ states and terminating collective cranking solutions for $I_{\text{max}}\!-\!2$. This example confirms that the onset of collectivity causes a uniform mixing of various angular momenta, regardless of individual features of specific nuclei. Indeed, in the studied nuclei, probabilities of finding the $I_{\text{max}}\!-\!2$ spin component within the $\vert\Phi_{I_{\text{max}}-2}\rangle=\sum_I w_I \vert I\rangle$ CHF deformed wave packets are $\vert{w}_{I_{\text{max}}-2}\vert^2 = 0.34\pm 0.05$, i.e., they extremely weakly depend on $N$ and $Z$. Moreover, values of $\vert{w}_{I_{\text{max}}-2}\vert^2$ appear to be very similar to $\vert{w}_{I_{\text{max}}}\vert^2$, which are equal to $0.35\pm 0.04$, and again almost do not change from one nucleus to another.

Situation changes quite radically for the unfavored-signature $[d_{3/2}^{-1} f_{7/2}^{n+1}]_{I_{\text{max}}-1}$ states. Within the CHF approximation, in $N\ne Z$ and $N\ne Z+1$ nuclei there are three $I_{\text{max}}\!-\!1$ configurations that can be created from the $I_{\text{max}}$ reference state. Indeed, this can be done by a signature-inverting $ph$ excitation involving either the neutron ($\nu$) or proton ($\pi$) $f_{7/2}$ particle, or the proton $d_{3/2}$ hole ($\bar\pi$), see Ref. [28]. The CHF solutions represent, therefore, mixtures of two physical $\vert I_{\text{max}}\!-\!1;I_{\text{max}}\!-\!1\rangle_i, i=1,2$, states with the spurious reorientation $\vert I_{\text{max}};I_{\text{max}}\!-\!1\rangle$ mode.

In such a case, the $I_y$ $\rightarrow$$I$ AMP scheme only removes the spurious mode, not affecting the mixing ratio of the two physical solutions $\vert I_{\text{max}}\!-\!1;I_{\text{max}}\!-\!1\rangle_i, \, i=1,2$. Hence, in contrast with the case of the $[f_{7/2}^{n}]_{I_{\text{max}}-1}$ states, quality of the results strongly depends on the quality of the underlying CHF field. The AMP results corresponding to the $\bar\pi$ CHF solutions, which in $^{42-45}$Sc, $^{44-46}$Ti, and $^{47}$V are the lowest in energy, show that the admixtures of spurious components are of the order of 10%, see the inset in Fig. 8. The obtained rotational corrections are, therefore, small -- of the order of 100 - 200keV, and the disagreement with data remains quite large, as shown in Fig. 8. We show these results only as an example of possible AMP calculations. However, for a complete analysis, one should, in principle, perform the GCM mixing of the AMP states corresponding to any possible CHF $I_{\text{max}}\!-\!1$ configuration. A study in this direction is left for the future work.

Figure 8: Energy differences between the $[d_{3/2}^{-1}f_{7/2}^{n+1}]_{I_{\text{max}}}$ terminating states and the lowest unfavored-signature terminating $d_{3/2}^{-1}f_{7/2}^{n+1}]_{I_{\text{max}}-1}$ states. Dots represent empirical data [32,33,34,35,36,37] and open and full diamonds represent the CHF and AMP results, respectively. Inset shows probabilities of finding the $I_{\text{max}}\!-\!1$ components within the lowest CHF solution $\vert\Phi_{I_{\text{max}}-1}\rangle$.