J. Dobaczewski, K. Bennaceur, F. Raimondi
July 17, 2012
A consistent formulation of the low-energy energy-density-functional (EDF) approach in terms of effective theory is long overdue in nuclear physics. Effective theories are now used in different domains of physics with a tremendous success. They quantify and formalize basic physical intuitions about aspects of the description that are essential, and those that can be treated in terms of controlled and correctible approximations. One spectacular example relates to derivations of nuclear forces based on the chiral perturbation theory augmented by the effective-field-theory treatment of corrective terms [1,2]. Analogous effective approach can also be applied in a much simpler context of quantal one-body dynamics [3].
Successful derivations from chiral effective field theory of
relativistic [4,5] and
nonrelativistic [6,7] nuclear EDFs were recently
accomplished. They lead to local EDFs with density-dependent
couplings associated with the underlying pion-exchange interaction.
These approaches strive to map out the in-medium nucleonic effects at
the two-pion-mass (2
![]() MeV/c
MeV/c![]() ) or Fermi-momentum
(
) or Fermi-momentum
(![]() MeV/
MeV/
![]() fm
fm![]() ) scales. However,
the energy scale of low-energy nuclear phenomena in finite nuclei is
much lower. For example, to dissociate a nucleon from a nucleus one
has to increase its kinetic energy by
) scales. However,
the energy scale of low-energy nuclear phenomena in finite nuclei is
much lower. For example, to dissociate a nucleon from a nucleus one
has to increase its kinetic energy by
![]() ,
that is, a typical separation energy of
,
that is, a typical separation energy of
![]() MeV corresponds to the momentum
increase of
MeV corresponds to the momentum
increase of
![]() MeV/
MeV/![]() . Moreover, the
low-energy EDFs are supposed to describe nuclear excitations and
shell-effects at even lower energies of 1MeV or
. Moreover, the
low-energy EDFs are supposed to describe nuclear excitations and
shell-effects at even lower energies of 1MeV or
![]() MeV/
MeV/![]() and below.
and below.
Therefore, what in the QCD-driven chiral dynamics is the small-energy scale, becomes a short-range high-energy scale of nucleon-nucleon force acting on relatively weakly bound nucleons in nuclei. The question of bridging these two different energy scales is the subject of current intense studies in nuclear physics [8]. In finite nuclei, surface effects decrease the infinite-matter particle binding energies by about a factor of two. In the present study, we aim at building a phenomenological low-energy EDFs, with gradient terms providing for the surface terms, corresponding the nuclear leptodermous expansion [9,10].
Ideas of the effective theory have recently been applied in constructing the EDFs based on higher-order derivatives of nuclear one-body densities [11]. When analyzed in terms of the density-matrix expansion [12], the obtained quasilocal EDFs converge fast with the order of derivatives [13], which is a very encouraging feature of the approach. The quasilocal EDFs are also obtained by the Hartree-Fock averaging of higher-order zero-range pseudopotentials [14].
However, one aspect of the approach developed so far is still missing, namely, the quasilocal EDFs and zero-range pseudopotentials do not provide us with any expansion scale, against which the higher-order derivatives could be classified. In the chiral effective field theory, such a scale is given by the cut-off energy in the momentum-space integrals, and allows for formulating a consistent power-counting scheme of the diagrammatic expansion [15]. In low-energy nuclear physics, an analogous cut-off regularization of the zero-range interactions has already been proposed [16,17], and the dimensional regularization was also studied [18], however, a consistent expansion scheme is not yet available.
In the present study, we introduce the expansion scale by employing
the regularized higher-order zero-range (pseudo)potentials - exactly
as it was illustrated in the simple examples discussed in
Ref. [3]. Among a plethora of various ways to regularize
delta interactions, we consider the one based on the Gaussian
function,
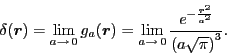 |
(1) |
In our definition of the pseudopotential (2), operators
![]() act on the product of the locality
delta functions
act on the product of the locality
delta functions
![]() and
regularized delta function
and
regularized delta function
![]() . Derivatives of
the delta functions have to be understood in the usual sense of
distributions, namely, when the pseudopotential (2) is
inserted into a matrix element, or when it is averaged with respect to
densities, the integration by parts transfers all derivatives onto
wave functions or densities. After the integration by parts, the
locality deltas reduce the integral to two variables,
. Derivatives of
the delta functions have to be understood in the usual sense of
distributions, namely, when the pseudopotential (2) is
inserted into a matrix element, or when it is averaged with respect to
densities, the integration by parts transfers all derivatives onto
wave functions or densities. After the integration by parts, the
locality deltas reduce the integral to two variables,
![]() and
and ![]() , only.
, only.
To give a specific example, up to the second-order, that is,
up to the next-to-leading-order (NLO) expansion, operators
![]() read
read
Before considering the general pseudopotential (2), let us
first assume that the differential operators
![]() depend only on the sum of relative momenta,
depend only on the sum of relative momenta,
![]() . At NLO,
this corresponds to equal second-order coupling constants,
. At NLO,
this corresponds to equal second-order coupling constants,
![]() . Such particular differential
operators commute with the locality deltas
. Such particular differential
operators commute with the locality deltas
![]() , and thus can
be applied directly onto the regularized delta
, and thus can
be applied directly onto the regularized delta
![]() . In such a case, pseudopotential (2)
reduces to a simple local potential
. In such a case, pseudopotential (2)
reduces to a simple local potential
Within the spirit of the effective theory, the series in
Eq. (5) is cut at a given
![]() .
Then, at a given fixed scale
.
Then, at a given fixed scale ![]() , coupling constant
, coupling constant ![]() have to be adjusted to data. If the expansion is relevant, the results
should only weakly depend on the regularization scale
have to be adjusted to data. If the expansion is relevant, the results
should only weakly depend on the regularization scale ![]() , provided
it is neither too large, when the expansion scale intrudes into the
physical scale of low-energy phenomena, nor too small, where
unresolved high-energy features are incorrectly described.
At any given order one can pick a specific scale
, provided
it is neither too large, when the expansion scale intrudes into the
physical scale of low-energy phenomena, nor too small, where
unresolved high-energy features are incorrectly described.
At any given order one can pick a specific scale ![]() where the
results agree best with the data.
where the
results agree best with the data.
Before such a complete program is carried out, in the present
exploratory study we use the fact that a successful parametrization of
the local potential already exists in the form of the Gogny
interaction [20,21], whose
finite-range part can be written as
At NLO (
![]() ), the eight coupling constants,
), the eight coupling constants,
![]() and
and ![]() , of the local regularized potential
(4) can be easily obtained from the eight parameters of the
central Gogny force,
, of the local regularized potential
(4) can be easily obtained from the eight parameters of the
central Gogny force, ![]() and
and ![]() . Indeed, at this
order, potentials (5) are combinations of a Gaussian and
Gaussian multiplied by
. Indeed, at this
order, potentials (5) are combinations of a Gaussian and
Gaussian multiplied by ![]() , which span similar sets of
functions as those of two Gaussians with two different ranges.
, which span similar sets of
functions as those of two Gaussians with two different ranges.
Below we use a prescription that can be
applied at any order
![]() , and which is based on global
characteristics of the potentials. Namely, we determine coupling
constants
, and which is based on global
characteristics of the potentials. Namely, we determine coupling
constants ![]() in Eq. (5) by requiring that the
lowest moments of both potentials are equal, that is,
in Eq. (5) by requiring that the
lowest moments of both potentials are equal, that is,
To determine properties of finite nuclei, in the present study we used the EDF approach for regularized potential defined in Eq. (4), along with the coupling constants (8) derived for the D1S Gogny force [21]. Numerical calculations were performed by implementing regularized potentials in the code HFODD (v2.53r) [22,23], which was adapted to solving self-consistent equations for finite-range interactions.
In Fig. 1, we present results of calculations
performed for eight doubly magic nuclei: ![]() O,
O, ![]() Ca,
Ca,
![]() Ca,
Ca, ![]() Ni,
Ni, ![]() Ni,
Ni, ![]() Sn,
Sn, ![]() Sn, and
Sn, and
![]() Pb. In each case, we show relative deviations of binding
energies (left panels) and rms radii (right panels) as compared to
values obtained with the original Gogny interaction. One can see
that with increasing order of expansion, the convergence is very
rapid; indeed, for every next order, the obtained relative deviations
decrease by about a factor of four, and at N
Pb. In each case, we show relative deviations of binding
energies (left panels) and rms radii (right panels) as compared to
values obtained with the original Gogny interaction. One can see
that with increasing order of expansion, the convergence is very
rapid; indeed, for every next order, the obtained relative deviations
decrease by about a factor of four, and at N![]() LO they are well
below 1%.
LO they are well
below 1%.
![\includegraphics[width=\columnwidth]{regdelta.fig1.eps}](img77.png)
|
We note here that the results presented in Fig. 1 were
obtained without any adjustment of parameters. However, one can expect
that such small adjustments can easily correct for
the smooth trends observed in Fig. 1. This is so because
binding energies of nuclei, which result form cancellations of the
kinetic and potential energies, are extremely sensitive to parameters
of the interaction. For example, we checked that modifications of the
Gogny density-dependent term of the order of 0.05% are able to bring
the N![]() LO mass of
LO mass of ![]() Pb exactly to the Gogny value.
Pb exactly to the Gogny value.
The regularized potentials proposed in this study (with or without
the restricted dependence on the relative momenta introduced
above), will later be used in extensive optimization procedures -
similarly as it has been done for other standard functionals used
within the EDF approaches. Nevertheless, even without such extensive
adjustments, basic features of the obtained effective theory can
already be illustrated by studying scaling properties of the results.
To this end, in Fig. 2 we show deviations of binding
energies and radii relative to those obtained for ![]() Pb. One can
see that the results scaled in this way are almost independent of the
regularization scale, which is an extremely encouraging result,
consistent with the effective-theory principles.
Pb. One can
see that the results scaled in this way are almost independent of the
regularization scale, which is an extremely encouraging result,
consistent with the effective-theory principles.
![\includegraphics[width=\columnwidth]{regdelta.fig2.eps}](img78.png)
|
Effective theories are built to provide us with expansions that converge better when the bound-state energy or scattering energy is lower. Spectacular examples of such a convergence pattern exist for weakly bound electron states in quantum mechanics of a one-body Coulomb problem [3] or for phase shifts of the two-body nucleon-nucleon scattering [2]. Convergence of an effective theory can be best visualized by the so-called Lepage plot [3], which shows the dependence of the error in the description of a given observable on energy. Such error should decrease with decreasing energy and with increasing order of expansion.
In many physical systems, scale of energy is inverted with respect to the scale of distance, that is, small distances correspond to large energies and vice versa. In finite nuclei, the situation is more complex, because the average energy per particle and average internucleon distance are almost constant throughout the mass chart, which is a simple consequence of the saturation of nuclear forces and near-constancy of density inside nuclei. Should then the effective theories work better in light (small) nuclei or in heavy (large) ones?
Good arguments in favor of the second option are provided by the density-matrix expansion (DME) [12], which uses the fact that the range of nuclear forces is smaller than characteristic distances at which densities in nuclei vary, see Refs. [24,13] and references cited therein, and by the ideas of the leptodermous expansion [9,10]. Indeed, since the largest variations of densities occur at nuclear surfaces, effective theories should work best in large nuclei, where the surface region is relatively small with respect to the nuclear bulk.
To study this
problem, in Fig. 3 we show reduced deviations of binding
energies,
![]() , and radii,
, and radii,
![]() , in function of the particle number
, in function of the particle number ![]() . This allows us to
compare results obtained for different nuclei in the same scale.
Since the relative deviations are almost independent of the
regularization scale
. This allows us to
compare results obtained for different nuclei in the same scale.
Since the relative deviations are almost independent of the
regularization scale ![]() (cf. Fig. 2), here we
plot them at
(cf. Fig. 2), here we
plot them at ![]() fm.
fm.
![\includegraphics[width=\columnwidth]{regdelta.fig3.eps}](img80.png)
|
We see that the results obtained for nuclei
beyond about ![]() scale with mass as those for
scale with mass as those for ![]() Pb. From the
point of view of the effective theory and proposed expansion, one can
interpret this result as a high similarity of these nuclei, that is,
their sizes are not different enough to induce significant
differences in their convergence properties, and they all would
appear at the same point of the Lepage plot. We also see that
properties of lighter nuclei, with
Pb. From the
point of view of the effective theory and proposed expansion, one can
interpret this result as a high similarity of these nuclei, that is,
their sizes are not different enough to induce significant
differences in their convergence properties, and they all would
appear at the same point of the Lepage plot. We also see that
properties of lighter nuclei, with ![]() , converge slightly
better than those of the heavier ones. However, only a future complete
analysis, performed for the entire mass table and for optimized
functionals, can here provide conclusive results.
, converge slightly
better than those of the heavier ones. However, only a future complete
analysis, performed for the entire mass table and for optimized
functionals, can here provide conclusive results.
We complete our analysis by discussing values of coupling constants
(8) in the so-called natural units, see
Refs. [25,26] and references cited therein.
Since the EDF generated by our regularized potential contains
only terms quadratic in densities, in the natural units
the coupling constants have the following dimensionless values,
Coupling constants ![]() (8) are plotted in
Fig. 4. Their almost-linear
(8) are plotted in
Fig. 4. Their almost-linear ![]() -dependence, which we see in
the logarithmic scale, allows us to derive the slope of this
dependence that corresponds to the value of
-dependence, which we see in
the logarithmic scale, allows us to derive the slope of this
dependence that corresponds to the value of
![]() MeV/
MeV/
![]() fm
fm![]() (dashed line).
For our regularized potentials at N
(dashed line).
For our regularized potentials at N![]() LO, we thus obtain a similar scale
LO, we thus obtain a similar scale
![]() as that characterizing the zero-range interactions at NLO
(
as that characterizing the zero-range interactions at NLO
(
![]() =2) [25,26]. Next, we fix the
normalization factor
=2) [25,26]. Next, we fix the
normalization factor ![]() so as to make the values of dimensionless
coupling constants
so as to make the values of dimensionless
coupling constants ![]() of the order of unity, which gives
of the order of unity, which gives
![]() MeV/
MeV/
![]() /(77MeV
/(77MeV![]() fm
fm![]() ).
As we see, this value is significantly smaller than the pion decay
constant
).
As we see, this value is significantly smaller than the pion decay
constant ![]() MeV/
MeV/
![]() , which normalizes
the EDFs derived directly from the chiral effective field
theory [25].
, which normalizes
the EDFs derived directly from the chiral effective field
theory [25].
![\includegraphics[width=0.7\columnwidth]{regdelta.fig4.eps}](img96.png)
|
![\includegraphics[width=\columnwidth]{regdelta.fig5.eps}](img100.png)
|
In our opinion, future prospects for using the proposed regularized (pseudo)potentials are high. First, similarly as in the simple one-body examples [3], they may present better convergence properties than similar expansions based on the zero-range interactions. Second, they allow for convergent summations of contributions from high single-particle momenta, which is not the case for zero-range interactions. And third, they allow for formulating a consistent expansion in terms of the orders of derivatives, with the convergence properties gauged against the regularization scale. This last feature is unique among all the EDF approaches based on zero-range and finite-range interactions developed so far, and gives us a potential of building an order-by-order correctible theory.
Interesting comments by Dick Furnstahl and Witek Nazarewicz are gratefully acknowledged. This work has been supported in part by the Academy of Finland and University of Jyväskylä within the FIDIPRO programme and by LEA COPIGAL Polish-French Collaboration Agreement. We acknowledge the CSC - IT Center for Science Ltd, Finland for the allocation of computational resources.