


Next: Angular-Momentum Projection
Up: ANGULAR-MOMENTUM PROJECTION OF CRANKED
Previous: ANGULAR-MOMENTUM PROJECTION OF CRANKED
Self-consistent mean-field method is practically the only formalism
allowing for large-scale computations in heavy, open-shell nuclei
with many valence particles. Inherent to the mean-field method is a
mechanism of the spontaneous symmetry breaking, which is essentially
the only way allowing to incorporate a significant part of many-body
correlations into a single intrinsic (symmetry-violating) Slater
determinant. Nuclear deformation and the emergence of rotational
bands after applying simple cranked mean-field approach, i.e., after an
approximate restoration of rotational invariance, is one of the most
spectacular and most intuitive manifestations of the spontaneous
symmetry breaking in nuclei.
An increasing quality of spectroscopic information demands more and more
accurate theory, pushing the efforts beyond the mean-field
approximation towards, in particular, symmetry-conserving formalisms
and symmetry restoration.[1,2,3] Hereby, we report on
development of a new theoretical tool allowing for the angular-momentum
projection (AMP) of cranked symmetry-unrestricted Slater determinants.
The standard method used to develop symmetry-conserving theory,
starting from intrinsic (deformed) wave function
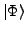 , obtained within the mean-field approach, is provided
by the projection techniques onto eigenspaces of symmetry
operators. There are two practical realizations of the projection
methods: more fundamental and elaborate variation after
projection (VAP) and slightly less advanced projection after
variation (PAV). In the past, many calculations have been performed
within the angular-momentum PAV method, where non-rotating states
have been projected, see, e.g., Refs.[4,5,6]
and the reviews in Refs.[2,3]. The cranking method provides
the first-order approximation to the angular-momentum VAP
method.[1] However, after the ground-breaking studies in
Refs.[7,8], calculations based on the AMP of
cranked states have not been performed. Here, we present the first
results of our recently developed AMP method of cranked
symmetry-unrestricted Hartree-Fock states. The procedure we use has been
implemented within the code HFODD
(v2.25b).[9,10,11,12]
, obtained within the mean-field approach, is provided
by the projection techniques onto eigenspaces of symmetry
operators. There are two practical realizations of the projection
methods: more fundamental and elaborate variation after
projection (VAP) and slightly less advanced projection after
variation (PAV). In the past, many calculations have been performed
within the angular-momentum PAV method, where non-rotating states
have been projected, see, e.g., Refs.[4,5,6]
and the reviews in Refs.[2,3]. The cranking method provides
the first-order approximation to the angular-momentum VAP
method.[1] However, after the ground-breaking studies in
Refs.[7,8], calculations based on the AMP of
cranked states have not been performed. Here, we present the first
results of our recently developed AMP method of cranked
symmetry-unrestricted Hartree-Fock states. The procedure we use has been
implemented within the code HFODD
(v2.25b).[9,10,11,12]
We determine the optimal product wave function 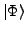 by using the
cranked self-consistent Skyrme-Hartree-Fock (SHF) method. The Ritz variational
principle:
by using the
cranked self-consistent Skyrme-Hartree-Fock (SHF) method. The Ritz variational
principle:
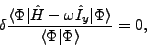 |
(1) |
is equivalent to a
variation of a local energy density functional (LEDF) with a supplementary
constraint on the average value of the projection of angular momentum
on the axis perpendicular to the symmetry axis (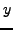 in our case). The
variation of LEDF in the isoscalar-isovector
in our case). The
variation of LEDF in the isoscalar-isovector 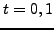 representation
(potential part) can be formally written as:
representation
(potential part) can be formally written as:
![\begin{displaymath}\delta
\mathcal{E}^{(Skyrme)}= \delta \sum_{t=0,1}\int d^3\ma...
...{H}_t^{(TE)}(\mathbf{r}) + \mathcal{H}_t^{(TO)}(\mathbf{r}) ].
\end{displaymath}](img18.png) |
(2) |
where
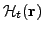 is expressed as a bilinear form of the
time-even (TE)
is expressed as a bilinear form of the
time-even (TE) 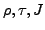 and
time-odd (TO)
and
time-odd (TO) 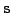 ,
, 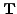 ,
, 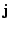 local densities
and currents, and by their derivatives,[13]
local densities
and currents, and by their derivatives,[13]
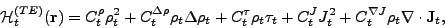 |
(3) |
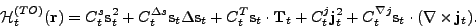 |
(4) |
By taking an expectation value of the Skyrme force over the Slater determinant,
one obtains the LEDF (3)-(4) with 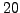 coupling
constants
coupling
constants 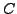 that are expressed uniquely through the 10 parameters
that are expressed uniquely through the 10 parameters
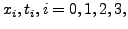 and
and 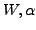 of the standard Skyrme force.
Because of the local gauge invariance of the Skyrme force, only 14 coupling
constants
of the standard Skyrme force.
Because of the local gauge invariance of the Skyrme force, only 14 coupling
constants 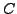 are independent quantities. The local gauge invariance links
three pairs of time-even and time-odd constants in the following way:
are independent quantities. The local gauge invariance links
three pairs of time-even and time-odd constants in the following way:
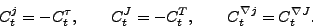 |
(5) |



Next: Angular-Momentum Projection
Up: ANGULAR-MOMENTUM PROJECTION OF CRANKED
Previous: ANGULAR-MOMENTUM PROJECTION OF CRANKED
Jacek Dobaczewski
2006-10-30
![]() , obtained within the mean-field approach, is provided
by the projection techniques onto eigenspaces of symmetry
operators. There are two practical realizations of the projection
methods: more fundamental and elaborate variation after
projection (VAP) and slightly less advanced projection after
variation (PAV). In the past, many calculations have been performed
within the angular-momentum PAV method, where non-rotating states
have been projected, see, e.g., Refs.[4,5,6]
and the reviews in Refs.[2,3]. The cranking method provides
the first-order approximation to the angular-momentum VAP
method.[1] However, after the ground-breaking studies in
Refs.[7,8], calculations based on the AMP of
cranked states have not been performed. Here, we present the first
results of our recently developed AMP method of cranked
symmetry-unrestricted Hartree-Fock states. The procedure we use has been
implemented within the code HFODD
(v2.25b).[9,10,11,12]
, obtained within the mean-field approach, is provided
by the projection techniques onto eigenspaces of symmetry
operators. There are two practical realizations of the projection
methods: more fundamental and elaborate variation after
projection (VAP) and slightly less advanced projection after
variation (PAV). In the past, many calculations have been performed
within the angular-momentum PAV method, where non-rotating states
have been projected, see, e.g., Refs.[4,5,6]
and the reviews in Refs.[2,3]. The cranking method provides
the first-order approximation to the angular-momentum VAP
method.[1] However, after the ground-breaking studies in
Refs.[7,8], calculations based on the AMP of
cranked states have not been performed. Here, we present the first
results of our recently developed AMP method of cranked
symmetry-unrestricted Hartree-Fock states. The procedure we use has been
implemented within the code HFODD
(v2.25b).[9,10,11,12]
![]() by using the
cranked self-consistent Skyrme-Hartree-Fock (SHF) method. The Ritz variational
principle:
by using the
cranked self-consistent Skyrme-Hartree-Fock (SHF) method. The Ritz variational
principle: