Fission barriers for the spherical $N$=184 isotones

Figure 5 shows the total binding energies and mass hexadecapole moments ($Q_{40}$) calculated for twelve even-even $N$=184 isotones as a function of the mass quadrupole moment $Q_{20}$. One can see that the $N$=184 systems are all spherical in their ground states (cf. Ref.[18] and references quoted therein). It has also been found that all of these SHE have reflection-symmetric static fission paths. Similarly, as for the deformed heavy nuclei discussed above, the mass hexadecapole moments along the fission path continually increase their values from 0 up to 80b$^2$.

The reduction of fission barriers due to the appearance of triaxial deformations, seen in Fig. 5 as the difference between the open and solid symbols, strongly depends on proton number. The largest effect has been predicted for the nucleus $^{310}126_{184}$ where the barrier reduction exceeds 3MeV. However, in the case of the isotones with $Z\leq 114$, triaxiality plays a minor role.

Studying static fission barriers can offer useful insights concerning the stability of SHE. Comparison of the sizes of static fission barriers in the $N$= 184 isotones shown in Fig. 5 hints at a possible increased stability against spontaneous fission for $^{302}118_{184}$ and $^{304}120_{184}$.

Figure 5: Similar as in Fig. 3 except for the even-even isotones with $N$=184.

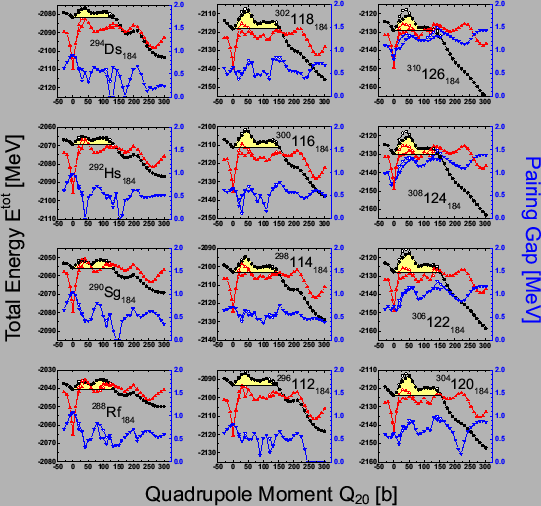
The neutron and proton pairing gaps calculated along the static fission paths for SHE with $N$=184 are shown in Fig. 6. The solid (open) symbols represent results obtained with (without) triaxial deformations. The values of pairing gaps in the spherical ground states correspond to the FRDM estimates[16]. As one can see, for all the SHE presented in Fig. 6, the average value of $\Delta_n$ fluctuates between 1 and 1.5MeV. On the other hand, the average $\Delta_p$ for all the isotones up to $^{304}120_{184}$ is around 0.5MeV. For the heaviest nuclei with $Z$= 122, 124, and 126, $\Delta_p$ steadily increases reaching the value of $\Delta_n$ for $^{310}126_{184}$. These results, obtained within the seniority pairing approximation, do not take into account the fact that structure of the single-particle orbitals may change along the fission paths. Such effects can be included by calculating pairing matrix elements from a zero-range pairing force, which will be the subject of a future analysis.

Figure 6: The total binding energies $E^{\mbox{\scriptsize{tot}}}$ ( $\mbox{\large$\bullet$}$, scales on the left-hand sides) and the neutron and proton pairing gaps (scales on the right-hand sides) for the $N$=184 isotones shown in Fig. 5. The differences between open and solid symbols illustrate the effects of triaxiality.