Next: MODEL STUDY Up: Isospin-invariant Skyrme energy-density-functional approach Previous: INTRODUCTION
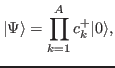 |
(1) |
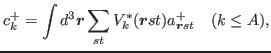 |
(2) |
To fix the notation, we now recall basic expressions introduced
and derived in Ref. [17].
The one-body density matrix
![]() is defined as
is defined as
![$\displaystyle \bar{H}[\hat{\rho}] = \int d^3\bbox{r}\, {\mathcal H}(\bbox{r})
= \int d^3\bbox{r}\, {\mathcal H}_{\rm Sk}(\bbox{r}) + E_{\rm Cou}[\hat{\rho}],$](img63.png) |
(4) |
Quasilocal densities ![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() , and
, and
![]() , are defined through the particle and spin non-local densities,
, are defined through the particle and spin non-local densities,
 |
(7) | |
 |
(8) |
![$\displaystyle = \frac{\delta \overline{H}[\hat{\rho}]}
{\delta \hat{\rho}(\bbox{r}st,\bbox{r}'s't')} $](img90.png) |
||
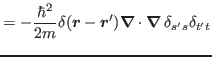 |
||
| (9) |
For the pnEDF depending on quasilocal densities only, such as in Eq. (6), the HF Hamiltonian is a local differential operator,
| (10) |
The resulting HF equation can be written as a self-consistent eigenvalue problem,
Jacek Dobaczewski 2014-12-07