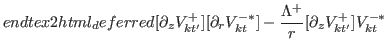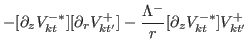We give the expression for particle density  , kinetic density
, kinetic density
 , spin density
, spin density  , spin-kinetic density
, spin-kinetic density 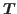 ,
current density
,
current density 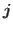 , and spin-current density
, and spin-current density 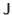 .
Tensor-kinetic density
.
Tensor-kinetic density 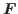 is not used and its expression is
omitted.
is not used and its expression is
omitted.
- (a)
- Scalar particle density
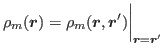 |
(21) |
where 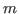 takes values 0, 1, 2 and 3. Suffix 0 represents
isoscalar component of the density
and 1 to 3 are the isovector components.
Expressing the density in terms of HFB wavefunctions (20), we obtain
takes values 0, 1, 2 and 3. Suffix 0 represents
isoscalar component of the density
and 1 to 3 are the isovector components.
Expressing the density in terms of HFB wavefunctions (20), we obtain
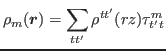 |
(22) |
where
![$\displaystyle \rho^{tt'}(rz) = \sum_{k}\biggl[ V^{+\ast}_{kt} V^{+}_{kt'}+V^{-\ast}_{kt} V^{-}_{kt'}\biggr],$](img229.png) |
(23) |
and we use the abbreviation of HFB wave functions
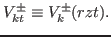 |
(24) |
Isospin components of the particle density are given by
The isospin structure of the particle density given by Eqs. (25)-(28) is identical
for all the following particle-hole
densities, and these expressions shall not be repeated in the following.
- (b)
- Kinetic density
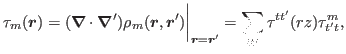 |
(29) |
where,
- (c)
- Pseudovector spin density
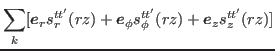 |
(31) |
where
- (d)
- Pseudovector spin-kinetic density
where
- (e)
- Vector current density
where
- (f)
- Tensor spin current density
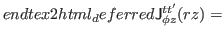 |
(37) |
Explicit expressions of the components are
 |
![$\displaystyle \frac{1}{2}\sum_{k}\biggr\{[\partial_{r} V^{+\ast}_{kt}]V^{-}_{kt'}-V^{+\ast}_{kt}[\partial_{r} V^{-}_{kt'}]$](img279.png) |
|
| |
![$\displaystyle -[\partial_{r} V^{-\ast}_{kt}]V^{+}_{kt'}+V^{-\ast}_{kt}[\partial_{r} V^{+}_{kt'}]\biggr\},$](img280.png) |
(38) |
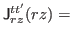 |
![$\displaystyle \frac{1}{2i}\sum_{k}\biggr\{[\partial_{r} V^{+\ast}_{kt}]V^{+}_{kt'}-V^{+\ast}_{kt}[\partial_{r} V^{+}_{kt'}]$](img282.png) |
|
| |
![$\displaystyle -[\partial_{r} V^{-\ast}_{kt}]V^{-}_{kt'}+V^{-\ast}_{kt}[\partial_{r} V^{-}_{kt'}]\biggr\},$](img283.png) |
(39) |
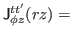 |
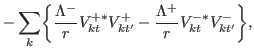 |
(40) |
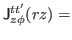 |
![$\displaystyle \frac{1}{2}\sum_{k}\biggr\{[\partial_{z} V^{+\ast}_{kt}]V^{-}_{kt'}-V^{+\ast}_{kt}[\partial_{z} V^{-}_{kt'}]$](img287.png) |
|
| |
![$\displaystyle -[\partial_{z} V^{-\ast}_{kt}]V^{+}_{kt'}+V^{-\ast}_{kt}[\partial_{z} V^{+}_{kt'}]\biggr\},$](img288.png) |
(41) |
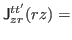 |
![$\displaystyle \frac{1}{2i}\sum_{k}\biggr\{[\partial_{z} V^{+\ast}_{kt}]V^{-}_{kt'}-V^{+\ast}_{kt}[\partial_{z} V^{-}_{kt'}]$](img290.png) |
|
| |
![$\displaystyle +[\partial_{z} V^{-\ast}_{kt}]V^{+}_{kt'}-V^{-\ast}_{kt}[ \partial_{z}V^{+}_{kt'}]\biggr\},$](img291.png) |
(42) |
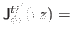 |
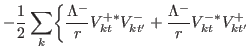 |
|
| |
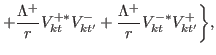 |
(43) |
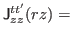 |
![$\displaystyle \frac{1}{2i}\sum_{k}\biggr\{[\partial_{z} V^{+\ast}_{kt}]V^{+}_{kt'}-V^{+\ast}_{kt}[ \partial_{z}V^{+}_{kt'}]$](img296.png) |
|
| |
![$\displaystyle -[\partial_{z} V^{-\ast}_{kt}]V^{-}_{kt'}+V^{-\ast}_{kt}[\partial_{z} V^{-}_{kt'}]\biggr\},$](img297.png) |
(44) |
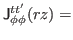 |
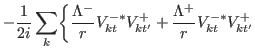 |
|
| |
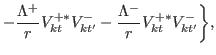 |
(45) |
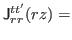 |
![$\displaystyle \frac{1}{2i}\sum_{k}\biggr\{[\partial_{r} V^{+\ast}_{kt}]V^{-}_{kt'}-V^{+\ast}_{kt}[\partial_{r} V^{-}_{kt'}]$](img302.png) |
|
| |
![$\displaystyle +[\partial_{r} V^{-\ast}_{kt}]V^{+}_{kt'}-V^{-\ast}_{kt}[\partial_{r} V^{+}_{kt'}]\biggr\}.$](img303.png) |
(46) |
The trace, antisymmetric, and symmetric parts of the tensor spin-current density are given by
Jacek Dobaczewski
2014-12-07
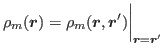
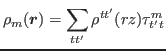
![$\displaystyle \rho^{tt'}(rz) = \sum_{k}\biggl[ V^{+\ast}_{kt} V^{+}_{kt'}+V^{-\ast}_{kt} V^{-}_{kt'}\biggr],$](img229.png)
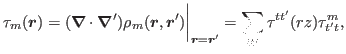
![$\displaystyle \sum_{k}\biggr\{
[\partial_{r} V^{+\ast}_{kt}][\partial_{r} V^{+}_{kt'}]
+[\partial_{r} V^{-\ast}_{kt}][ \partial_{r}V^{-}_{kt'}]$](img246.png)
![$\displaystyle + [\partial_{z} V^{+\ast}_{kt}][\partial_{z} V^{+}_{kt'}]
+[\partial_{z} V^{-\ast}_{kt}][ \partial_{z} V^{-}_{kt'}]\biggr\} .$](img248.png)
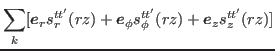
![$\displaystyle \sum_{k}\biggr\{ \bbox{e}_{r}[V^{-\ast}_{kt} V^{+}_{kt'}
+V^{+\ast}_{kt} V^{-}_{kt'}]$](img252.png)
![$\displaystyle + \bbox{e}_{\phi}i[V^{+\ast}_{kt} V^{-}_{kt'}-V^{-\ast}_{kt} V^{+}_{kt'}]$](img253.png)
![$\displaystyle + \bbox{e}_{z}[ V^{+\ast}_{kt} V^{+}_{kt'} -V^{-\ast}_{kt} V^{-}_{kt'}]\biggr\}.$](img254.png)
![$\displaystyle \biggr[(\bbox{\nabla} \cdot \bbox{\nabla} ')\bbox{s}_m(\bbox{r}, \bbox{r}') \biggr]_{ \bbox{r} = \bbox{r}'} $](img256.png)
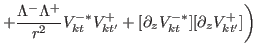
![$\displaystyle \sum_{k}\biggr\{ \bbox{e}_{r}\biggr( [\partial_{r}V^{+\ast}_{kt}]...
...al_{r} V^{-}_{kt'}]+\frac{\Lambda^{+}\Lambda^{-}}{r^2}V^{+\ast}_{kt}V^{-}_{kt'}$](img259.png)
![$\displaystyle + \frac{\Lambda^{-}\Lambda^{+}}{r^2}V^{-\ast}_{kt}V^{+}_{kt'}+[\partial_{z} V^{-\ast}_{kt}][ \partial_{z} V^{+}_{kt'}]\biggr)$](img261.png)
![$\displaystyle +i\bbox{e}_{\phi}\biggr( [\partial_{r} V^{+\ast}_{kt}][\partial_{r} V^{-}_{kt'}]+\frac{\Lambda^{-}\Lambda^{+}}{r^2}V^{+\ast}_{kt}V^{-}_{kt'} $](img262.png)
![$\displaystyle +\bbox{e}_z\biggr([\partial_{r} V^{+\ast}_{kt}][\partial_{r} V^{+}_{kt'}]+\frac{\Lambda^{-2}}{r^2}V^{+\ast}_{kt}V^{+}_{kt'} $](img265.png)
![$\displaystyle +[\partial_{z} V^{+\ast}_{kt}][\partial_{z} V^{+}_{kt}]-[\partial_{r} V^{-\ast}_{kt}][ \partial_{r} V^{-}_{kt'}] $](img266.png)
![$\displaystyle - \frac{\Lambda^{+2}}{r^2}V^{-\ast}_{kt}V^{-}_{kt'}-[\partial_{z} V^{-\ast}_{kt}][ \partial_{z}V^{-}_{kt'}]\biggr) \biggr\}.$](img267.png)
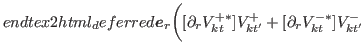
![$\displaystyle \frac{1}{2i}\biggr[(\bbox{\nabla}-\bbox{\nabla}')\rho_{m}(\bbox{r}, \bbox{r}')\biggr]_{\bbox{r}=\bbox{r}'} $](img269.png)
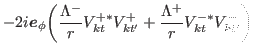
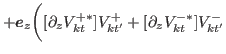
![$\displaystyle \frac{1}{2i}\sum_{k}\biggr\{ \bbox{e}_r\biggr([\partial_{r} V^{+\ast}_{kt}]V^{+}_{kt'}+[\partial_{r} V^{-\ast}_{kt}] V^{-}_{kt'}$](img272.png)
![$\displaystyle - V^{+\ast}_{kt}[\partial_{z} V^{+}_{kt'}]-V^{-\ast}_{kt} [\partial_{z} V^{-}_{kt'}]\biggr) \biggr\}.$](img276.png)
![$\displaystyle \frac{1}{2}\sum_{k}\biggr\{[\partial_{r} V^{+\ast}_{kt}]V^{-}_{kt'}-V^{+\ast}_{kt}[\partial_{r} V^{-}_{kt'}]$](img279.png)
![$\displaystyle -[\partial_{r} V^{-\ast}_{kt}]V^{+}_{kt'}+V^{-\ast}_{kt}[\partial_{r} V^{+}_{kt'}]\biggr\},$](img280.png)
![$\displaystyle \frac{1}{2i}\sum_{k}\biggr\{[\partial_{r} V^{+\ast}_{kt}]V^{+}_{kt'}-V^{+\ast}_{kt}[\partial_{r} V^{+}_{kt'}]$](img282.png)
![$\displaystyle -[\partial_{r} V^{-\ast}_{kt}]V^{-}_{kt'}+V^{-\ast}_{kt}[\partial_{r} V^{-}_{kt'}]\biggr\},$](img283.png)
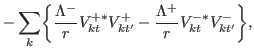
![$\displaystyle \frac{1}{2}\sum_{k}\biggr\{[\partial_{z} V^{+\ast}_{kt}]V^{-}_{kt'}-V^{+\ast}_{kt}[\partial_{z} V^{-}_{kt'}]$](img287.png)
![$\displaystyle -[\partial_{z} V^{-\ast}_{kt}]V^{+}_{kt'}+V^{-\ast}_{kt}[\partial_{z} V^{+}_{kt'}]\biggr\},$](img288.png)
![$\displaystyle \frac{1}{2i}\sum_{k}\biggr\{[\partial_{z} V^{+\ast}_{kt}]V^{-}_{kt'}-V^{+\ast}_{kt}[\partial_{z} V^{-}_{kt'}]$](img290.png)
![$\displaystyle +[\partial_{z} V^{-\ast}_{kt}]V^{+}_{kt'}-V^{-\ast}_{kt}[ \partial_{z}V^{+}_{kt'}]\biggr\},$](img291.png)
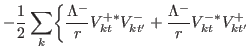
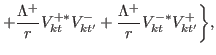
![$\displaystyle \frac{1}{2i}\sum_{k}\biggr\{[\partial_{z} V^{+\ast}_{kt}]V^{+}_{kt'}-V^{+\ast}_{kt}[ \partial_{z}V^{+}_{kt'}]$](img296.png)
![$\displaystyle -[\partial_{z} V^{-\ast}_{kt}]V^{-}_{kt'}+V^{-\ast}_{kt}[\partial_{z} V^{-}_{kt'}]\biggr\},$](img297.png)
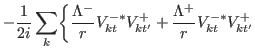
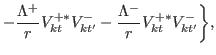
![$\displaystyle \frac{1}{2i}\sum_{k}\biggr\{[\partial_{r} V^{+\ast}_{kt}]V^{-}_{kt'}-V^{+\ast}_{kt}[\partial_{r} V^{-}_{kt'}]$](img302.png)
![$\displaystyle +[\partial_{r} V^{-\ast}_{kt}]V^{+}_{kt'}-V^{-\ast}_{kt}[\partial_{r} V^{+}_{kt'}]\biggr\}.$](img303.png)