HFB calculations

The HFB method was used. Four parameter sets of the Skyrme interaction were taken in the particle-hole channel: SLy4[8], SkM*[9], SkP[10], and SIII[11]. For the description of pairing, procedures of Ref.[12] were followed. The density-dependent delta interaction in the form of

$$V(\vec{r}_1,\vec{r}_2)=V_0\left(1-\frac{\rho(\vec{r}_1)}{2\rho_0}\right)\delta(\vec{r}_1-\vec{r}_2)$$ (1)

was employed, with the saturation density, $\rho_0$=0.16fm$^{-3}$, and strengths of $V_0$=$-$285.88, $-$233.94, $-$213.71, and $-$249.04MeVfm$^3$ for SLy4, SkM*, SkP, and SIII, respectively. The densities were constructed out of quasi-particle states with equivalent-spectrum energies[10] up to 60MeV. In order to study effects of pairing, the HF calculations were also performed for comparison. Reflection symmetries in two or three perpendicular planes were imposed, correspondingly, when looking for the tetrahedral and quadrupole solutions. The calculations were carried out by using the code HFODD (v2.11k)[13,14], which expands the quasi-particle wave-functions onto the Harmonic-Oscillator basis. Bases of 14 and 16 spherical shells were taken for the Zr and heavier elements, respectively.

Six nuclei, doubly-magic with respect to the tetrahedral magic numbers, were examined: $^{80}_{40}$Zr$_{40}$, $^{98}_{40}$Zr$_{58}$, $^{110}_{40}$Zr$_{70}$, $^{126}_{56}$Ba$_{70}$, $^{160}_{70}$Yb$_{90}$, and $^{226}_{90}$Th$_{136}$. In all of them, the HF and HFB energy minima corresponding to the tetrahedral shapes were found with all the examined forces, apart from a few exceptions. The found solutions are characterized by the $\beta _{32}$ deformations ranging from 0.08 to 0.26, and admixtures of $\beta_{40}$ and $\beta_{44}$ deformations in proportions that preserve the tetrahedral symmetry[3], and with values of $\beta_{40}$ ranging from about 0.01 to 0.07. Deformations of higher multipolarities were found to be negligibly small. As expected for the tetrahedral symmetry, the HF s.p. and HFB quasi-particle spectra are composed of two-fold and four-fold degenerate levels. In the six nuclei in question, spherical, oblate, prolate, and triaxial solutions were also found, depending on the nucleus, as discussed below.

Figure 1: Total energy in function of the tetrahedral deformation $\beta _{32}$ in $^{110}$Zr, obtained from the HFB calculations with the SIII force. $\Delta E_{sh}$ denotes the energy difference between the spherical point and the tetrahedral minimum.

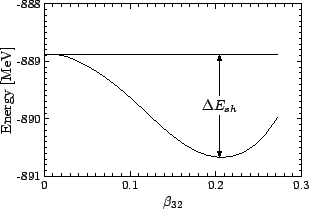Three quantities that characterize the obtained tetrahedral solutions will be examined: the energy difference, $\Delta E_{hq}$, between the tetrahedral ($h$) and lowest quadrupole ($q$) minima, the energy difference, $\Delta E_{sh}$, between the spherical point ($s$) and tetrahedral minimum, and the deformation $\beta _{32}$. $\Delta E_{hq}$ gives an idea of the excitation energy of the tetrahedral states above the ground state. $\Delta E_{sh}$ is important for the following reason. Both from the previous self-consistent studies in $^{80}$Zr[6,7], as well as from our preliminary results for $^{80,98,110}$Zr, it seems that, at least in the Zr isotopes, there is no energy barrier between the spherical and tetrahedral solutions. Energy in function of $\beta _{32}$ looks rather like the dependence shown in Fig. 1, obtained from the HFB calculations in $^{110}$Zr with the SIII force. One can see that $\Delta E_{sh}$ measures the depth of the tetrahedral minimum against changes in $\beta _{32}$, and thus provides information on whether a stable tetrahedral deformation or rather tetrahedral vibrations about the spherical shape should be expected.

Figure 2: The HF (circles, lower-case labels) and HFB (plus symbols, upper-case labels) energy minima marked on the $\beta _2$-$E$ plane for selected nuclei and forces, as specified in each panel. The tetrahedral ($h$, $H$), spherical ($s$, $S$), oblate ($O$), prolate ($P$), and triaxial ($T$) solutions are shown.

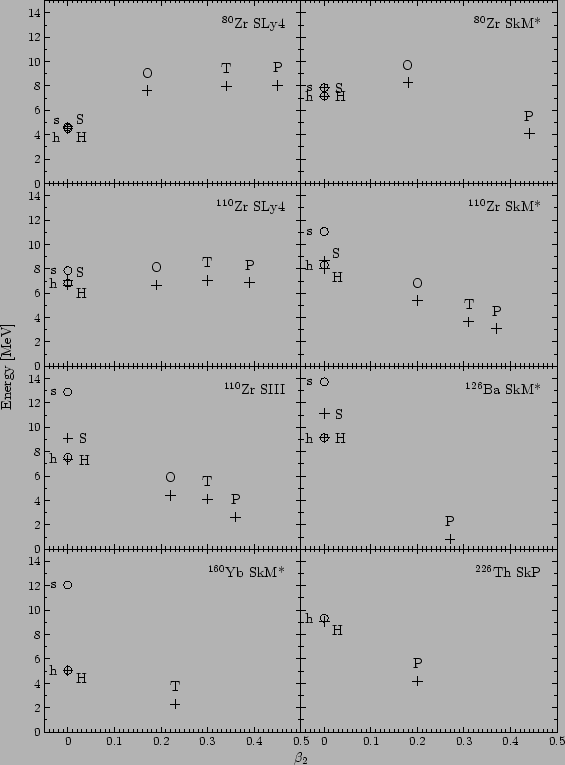Figure 2 shows the energy minima for selected nuclei and forces as points on the $\beta _2$-$E$ plane. In each panel, all the found HFB solutions (plus symbols, upper-case labels) are shown, while the HF solutions (circles, lower-case labels), are given only for the tetrahedral and spherical cases. The labels denote the tetrahedral ($h$, $H$), spherical ($s$, $S$), oblate ($O$), prolate ($P$), and triaxial ($T$) solutions.

One of the principal observations resulting from our calculations is that various Skyrme forces may give significantly different energetical positions of the tetrahedral solutions with respect to the quadrupole minima. This is most pronounced for the SLy4 and SkM* results in $^{80}$Zr (two upmost panels in Fig. 2), which give the tetrahedral minima of about 3MeV below and above the lowest quadrupole state, respectively. The extremal values of $\Delta E_{hq}$ predicted by various forces for each nucleus studied here are collected in Table 1. They do not depend much on whether pairing is included or not. The differences between the maximum and minimum values are of the order of a few MeV. One can see, nevertheless, that $\Delta E_{hq}$ is lowest in Zr isotopes, where some forces even predict the tetrahedral solution to be the ground state. Values of $\Delta E_{hq}$ are particularly large, not smaller than 7MeV, in $^{126}$Ba and rather moderate, even about 3MeV, in $^{160}$Yb and $^{226}$Th.

Table 1: Minimum (min) and maximum (max) values of $\Delta E_{hq}$ [MeV], $\Delta E_{sh}$ [MeV], and $\beta _{32}$ from among the HF or HFB results obtained for each studied nucleus with the SLy4, SkM*, SkP, and SIII Skyrme forces, denoted by superscripts $y$, $m$, $p$, and $i$, respectively.

	$\Delta E_{hq}$		$\Delta E_{sh}$				$\beta _{32}$
	HFB		HF		HFB		HF		HFB
Nucleus	min	max	min	max	min	max	min	max	min	max
$^{80}$Zr	-3$^y$	3$^m$	0.1$^y$	2$^i$	0.1$^y$	2$^i$	0.11$^y$	0.20$^i$	0.11$^y$	0.20$^i$
$^{98}$Zr	-1.5$^m$	2$^i$	0.3$^y$	0.7$^m$	0.04$^y$	0.5$^m$	0.14$^y$	0.16$^m$	0.09$^y$	0.20$^i$
$^{110}$Zr	-0.4$^y$	5$^m$	0.07$^p$	5$^i$	0.4$^y$	2$^i$	0.08$^p$	0.23$^i$	0.14$^y$	0.21$^i$
$^{126}$Ba	7$^p$	11$^i$	3$^y$	5$^m$	2$^m$	2$^m$	0.17$^p$	0.26$^i$	0.22$^m$	0.22$^m$
$^{160}$Yb	3$^m$	7$^i$	3$^y$	7$^m$			0.19$^p$	0.26$^i$	0.23$^m$	0.24$^i$
$^{226}$Th	3$^m$	8$^y$					0.18$^p$	0.24$^i$	0.15$^p$	0.22$^m$

Further important point is that the depths of the tetrahedral minima, $\Delta E_{sh}$, are reduced by pairing. This can be seen from the comparison of the HF and HFB results for $^{110}$Zr and $^{126}$Ba (four central panels in Fig. 2). The reductions may be as significant as from 3 to 1MeV in $^{110}$Zr with SkM*, while for SkP the inclusion of pairing suppresses the tetrahedral minimum in $^{110}$Zr altogether. The decrease in $\Delta E_{sh}$ is mainly due to the lowering of the energy at the spherical point, i.e., the pairing influences the spherical state more than the tetrahedral one. This is so because the s.p. energy gaps at the Fermi level are bigger in the latter case, as already discussed in the Introduction. In $^{80}$Zr with SIII, for instance, pairing vanishes at the tetrahedral minimum, and remains non-zero at the spherical point. Predictions concerning the destructive role of pairing strongly depend on the details of the method, as well. The HF+BCS [6] and HFB[7] calculations for $^{80}$Zr, both using the SIII force, yielded $\Delta E_{sh}$ of 0.7MeV and several tens of keV, respectively. The corresponding result of our calculations is about 2MeV.

In the current analysis, we also obtain differences in predictions of various Skyrme forces as to the values of $\Delta E_{sh}$, both with and without pairing. In the HFB results for $^{110}$Zr, for example, $\Delta E_{sh}$ varies from about 0.4 for SLy4 to 2MeV for SIII, not counting SkP. The HF and HFB results for other studied nuclei are summarized in Table 1. In $^{226}$Th, no spherical solutions, and in $^{160}$Yb no spherical HFB solutions were found, so that the corresponding values of $\Delta E_{sh}$ could not be calculated. In $^{126}$Ba, the tetrahedral HFB solution was obtained with only one force, SkM*. However, the HF results exhibit a clear trend that $\Delta E_{sh}$ increases with the mass number. It can be as small as a few tens of keV in Zr isotopes, and as large as 7MeV for $^{160}$Yb with SkM*. The problem of stability of the tetrahedral minima can be even more complicated because of a possible softness of the nuclei in question against the octupole deformations other than $\beta _{32}$[6,7].

The four Skyrme forces used in our study also give somewhat different values of the $\beta _{32}$ deformation, see Table 1. The inclusion of pairing slightly reduces these values, along with $\Delta E_{sh}$. Heavier isotopes have larger values of $\beta _{32}$.