


Next: Interpretation of polarizing field
Up: Hartree-Fock-Bogoliubov Theory of Polarized
Previous: Signature symmetry
Two Fermi Level Approach
The main idea behind the 2FLA [7,10] is
to force a nonzero spin polarization in the system by finding the
ground-state condensate in the presence of an external field that favors one
spin over the other.
In the language of signature, ``spin-up" corresponds to 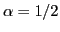 while ``spin-down" corresponds to
while ``spin-down" corresponds to 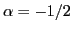 .
The polarization is achieved by adding to the Hamiltonian the
single-particle field
.
The polarization is achieved by adding to the Hamiltonian the
single-particle field
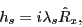 |
(23) |
i.e., constructing the Routhian (9), 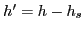 .
The imaginary unit must be put in the definition of
.
The imaginary unit must be put in the definition of 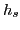 , because in
the single-particle space
, because in
the single-particle space 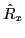 is antihermitian. Consequently,
is antihermitian. Consequently,
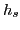 is time-odd, cf. Eq. (16).
Since
is time-odd, cf. Eq. (16).
Since 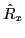 and the quasiparticle Hamiltonian commute, adding
and the quasiparticle Hamiltonian commute, adding 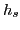 represents a non-collective cranking; hence, the quasiparticle
routhians must be linear in
represents a non-collective cranking; hence, the quasiparticle
routhians must be linear in 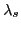 .
.
The field (26)
will raise the Fermi energy 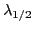 of the subsystem having signature
of the subsystem having signature
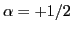 by an amount
by an amount 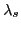 and lower the Fermi energy
and lower the Fermi energy
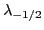 of
the
of
the 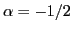 subsystem by the same amount. The relations
between chemical potentials in 2FLA read:
subsystem by the same amount. The relations
between chemical potentials in 2FLA read:
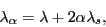 |
(24) |
where
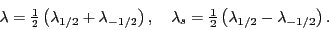 |
(25) |
The HFB Routhian matrix of 2FLA can be written as [7]
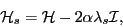 |
(26) |
where 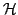 is the matrix (19) corresponding to
is the matrix (19) corresponding to
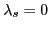 and
and 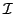 is the unit matrix.
is the unit matrix.
Since the added term is proportional to the unit matrix, its only effect is
to shift the HFB eigenvalues up or down,
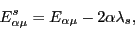 |
(27) |
where 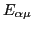 are the eigenvalues of
are the eigenvalues of 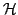 .
Therefore, when plotted as a function of
.
Therefore, when plotted as a function of 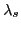 , the
energies
, the
energies
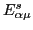 are straight lines with
slopes
are straight lines with
slopes 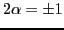 ,
as schematically depicted in Fig. 2.
The Hamiltonian (19)
usually represents an unpolarized system, in which case the quasiparticle
energies
,
as schematically depicted in Fig. 2.
The Hamiltonian (19)
usually represents an unpolarized system, in which case the quasiparticle
energies 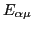 are degenerate (Fig. 2, top). If
are degenerate (Fig. 2, top). If 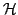 has
time-odd fields (due, e.g., to an external magnetic field or nonzero
angular velocity), this Kramers degeneracy is lifted (Fig. 2, bottom).
has
time-odd fields (due, e.g., to an external magnetic field or nonzero
angular velocity), this Kramers degeneracy is lifted (Fig. 2, bottom).
Figure 2:
(Color online)
One-quasiparticle levels of both signatures
(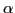 =1/2: solid line;
=1/2: solid line; 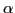 =-1/2: dotted line)
as functions of
=-1/2: dotted line)
as functions of 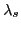 for a HFB
Hamiltonian (19) without (top) and with (bottom)
time-odd fields. In the latter case, the Kramers degeneracy at
for a HFB
Hamiltonian (19) without (top) and with (bottom)
time-odd fields. In the latter case, the Kramers degeneracy at
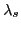 =0 is lifted, i.e., states
=0 is lifted, i.e., states
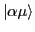 and
and
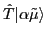 have different energies.
The negative energy levels occupied in the quasiparticle vacuum
are marked by thick lines. At the points
have different energies.
The negative energy levels occupied in the quasiparticle vacuum
are marked by thick lines. At the points
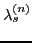 marked
by stars, the quasiparticle level
marked
by stars, the quasiparticle level 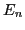 with
with 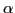 =1/2 becomes occupied.
If this level is not degenerate, or its degeneracy is an odd integer,
the particle-number parity
=1/2 becomes occupied.
If this level is not degenerate, or its degeneracy is an odd integer,
the particle-number parity 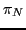 of the vacuum changes
as indicated.
of the vacuum changes
as indicated.
|
|
Subsections



Next: Interpretation of polarizing field
Up: Hartree-Fock-Bogoliubov Theory of Polarized
Previous: Signature symmetry
Jacek Dobaczewski
2009-04-13
![]() of the subsystem having signature
of the subsystem having signature
![]() by an amount
by an amount ![]() and lower the Fermi energy
and lower the Fermi energy
![]() of
the
of
the ![]() subsystem by the same amount. The relations
between chemical potentials in 2FLA read:
subsystem by the same amount. The relations
between chemical potentials in 2FLA read:
![\includegraphics[trim=0cm 0cm 0cm 0cm,width=0.4\textwidth,clip]{fig2.eps}](img128.png)