


Next: Conclusions
Up: Hartree-Fock-Bogoliubov Theory of Polarized
Previous: Particle-number parity of the
Atomic and nuclear HFB calculations
The first numerical example of 2FLA deals with a two-component
polarized atomic condensate in a deformed harmonic trap using the
superfluid local density approximation [34,10]. The system is
described by a local energy density
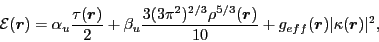 |
(30) |
where the local densities
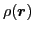 (particle density),
(particle density),
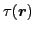 (kinetic energy density),
and
(kinetic energy density),
and
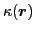 (pairing tensor)
are constructed from the quasiparticle HFB wave functions.
The parameters
(pairing tensor)
are constructed from the quasiparticle HFB wave functions.
The parameters 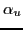 ,
, 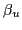 , and
the effective pairing strength
, and
the effective pairing strength
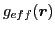 have been taken according to
Ref. [10]. We assume that the external trapping potential can be described
by an axially deformed harmonic oscillator with frequencies [17]
have been taken according to
Ref. [10]. We assume that the external trapping potential can be described
by an axially deformed harmonic oscillator with frequencies [17]
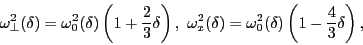 |
(31) |
with
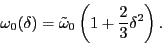 |
(32) |
As in Ref. [10], we put
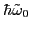 =1.
=1.
The calculations were carried out for systems with 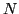 =30 and 31 fermions
in a spherical (
=30 and 31 fermions
in a spherical (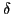 =0) and deformed (
=0) and deformed (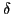 =0.2) trap.
The HFB equations were solved by using the recently developed
axial DFT solver HFB-AX [35].
The results are displayed in Fig. 3.
=0.2) trap.
The HFB equations were solved by using the recently developed
axial DFT solver HFB-AX [35].
The results are displayed in Fig. 3.
Figure 3:
(Color online)
Quasiparticle levels
(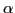 =1/2: solid line;
=1/2: solid line; 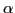 =-1/2: dotted line)
as functions of
=-1/2: dotted line)
as functions of 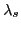 for
a two-component
polarized atomic condensate in a deformed harmonic trap using the
superfluid local density approximation [34,10].
The calculations were carried out for
for
a two-component
polarized atomic condensate in a deformed harmonic trap using the
superfluid local density approximation [34,10].
The calculations were carried out for 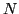 =30
(left) and
=30
(left) and 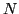 =31 (right). The top panels correspond to the spherical
case (
=31 (right). The top panels correspond to the spherical
case (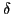 =0).
Here the quasiparticle levels are labeled with the usual spectroscopic
designation of orbital angular momentum
=0).
Here the quasiparticle levels are labeled with the usual spectroscopic
designation of orbital angular momentum 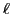 . Each line represents a
set of (2
. Each line represents a
set of (2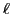 +1)-fold degenerate states.
In the deformed case (
+1)-fold degenerate states.
In the deformed case (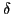 =0.2; middle panels)
the levels with the opposite values of
=0.2; middle panels)
the levels with the opposite values of 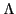
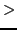 0 are two-fold degenerate.
The corresponding values of
0 are two-fold degenerate.
The corresponding values of 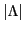 ere shown in the inset.
The Kramers degeneracy can be lifted by adding a cranking term,
ere shown in the inset.
The Kramers degeneracy can be lifted by adding a cranking term,
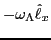 to the Hamiltonian (bottom panels,
to the Hamiltonian (bottom panels,
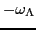 =0.05). Here, every level is labeled by the
=0.05). Here, every level is labeled by the
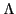 quantum number, see the inset.
In order to make the plot less busy, the
quasiparticle levels originating from very excited spherical
quantum number, see the inset.
In order to make the plot less busy, the
quasiparticle levels originating from very excited spherical
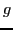 ,
, 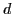 , and
, and 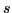 shells are not shown in the two lower panels.
See text for details.
shells are not shown in the two lower panels.
See text for details.
|
|
In the spherical case, Fig.3 (top), the spin degeneracy is lifted by the polarizing
field 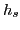 . However, as discussed in Sec. 3.2, the orbital
. However, as discussed in Sec. 3.2, the orbital
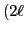 +1)-fold degeneracy is present. Consequently, after the crossing
point, the vacuum becomes a
+1)-fold degeneracy is present. Consequently, after the crossing
point, the vacuum becomes a 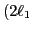 +1)-quasiparticle state, where
+1)-quasiparticle state, where
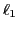 is the orbital angular momentum of the lowest quasiparticle level.
For
is the orbital angular momentum of the lowest quasiparticle level.
For 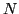 =30, the lowest quasiparticle excitation is a
=30, the lowest quasiparticle excitation is a 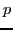 state, i.e.,
above the crossing point the local HFB vacuum becomes a three-quaspiarticle
state.
At the crossing point, the self-consistent mean-field
changes abruptly. In particular,
the chemical potential
moves up as the number of particles increases by one,
and the pairing gap decreases due to blocking.
This produces a sharp discontinuity around the crossing point, which can be seen
in all three cases presented in Fig. 3.
state, i.e.,
above the crossing point the local HFB vacuum becomes a three-quaspiarticle
state.
At the crossing point, the self-consistent mean-field
changes abruptly. In particular,
the chemical potential
moves up as the number of particles increases by one,
and the pairing gap decreases due to blocking.
This produces a sharp discontinuity around the crossing point, which can be seen
in all three cases presented in Fig. 3.
The middle portion of Fig. 3 illustrates the deformed case. Here,
quasiparticle states are labeled using the angular momentum projection
quantum number 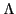 onto the symmetry axis of the trapping potential (
onto the symmetry axis of the trapping potential (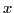 -axis).
Because of the Kramers degeneracy, levels with
-axis).
Because of the Kramers degeneracy, levels with 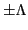 are degenerate.
That is, except for
are degenerate.
That is, except for 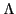 =0, each quasiparticle state is two-fold
degenerate. In the case presented in Fig. 3, the two lowest levels have
=0, each quasiparticle state is two-fold
degenerate. In the case presented in Fig. 3, the two lowest levels have
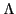 =0, hence they are associated with one-quasiparticle excitations. The third
state has
=0, hence they are associated with one-quasiparticle excitations. The third
state has 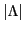 =1, and its crossing does not change
the particle-number parity of the HFB vacuum.
=1, and its crossing does not change
the particle-number parity of the HFB vacuum.
The two-fold Kramers degeneracy can be removed by adding an external
orbital-polarizing field,
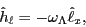 |
(33) |
where
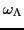 is the cranking frequency for the orbital
motion. Indeed, in the absence of the spin-orbit coupling
the spin and the orbital angular momentum may rotate with different
angular velocities. In the presence of
the field (36), each level is shifted by
is the cranking frequency for the orbital
motion. Indeed, in the absence of the spin-orbit coupling
the spin and the orbital angular momentum may rotate with different
angular velocities. In the presence of
the field (36), each level is shifted by
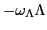 ,
i.e., the energy splitting of the Kramers doublet becomes
,
i.e., the energy splitting of the Kramers doublet becomes
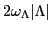 . An illustrative
example of such situation is displayed in the bottom panels of Fig. 3.
Here, each level corresponds to a one-quasiparticle excitation.
We confirmed numerically that the result of calculations
for
. An illustrative
example of such situation is displayed in the bottom panels of Fig. 3.
Here, each level corresponds to a one-quasiparticle excitation.
We confirmed numerically that the result of calculations
for 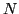 =31 by explicitly blocking the lowest
level are here equivalent to those
with 2FLA carried out above the crossing. It is seen in Fig. 3, however,
that because of high density of quasiparticle levels, the self-consistent
calculations in 2FLA are difficult due to many consecutive crossings
that make it extremely difficult to keep track of the fixed configuration.
We note that the order of the quasiparticle levels in
=31 by explicitly blocking the lowest
level are here equivalent to those
with 2FLA carried out above the crossing. It is seen in Fig. 3, however,
that because of high density of quasiparticle levels, the self-consistent
calculations in 2FLA are difficult due to many consecutive crossings
that make it extremely difficult to keep track of the fixed configuration.
We note that the order of the quasiparticle levels in 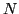 =30 and
=30 and 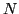 =31 systems
is affected by the variation of the mean field due to the crossing.
=31 systems
is affected by the variation of the mean field due to the crossing.
In order to illustrate 2FLA in the nuclear case, we carried out nuclear DFT
calculations using the Skyrme energy density functional SLy4
[36] in the p-h channel, augmented by the
``mixed-pairing" [37] density-dependent delta functional in the p-p
channel.
The details pertaining to the numerical details, e.g. the pairing
space employed, can be found in Ref. [35].
As a representative example, we took the pair of deformed nuclei
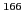 Er (
Er (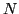 =98) and
=98) and 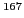 Er (
Er (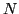 =99). The
pairing strength
=99). The
pairing strength 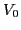 =-320 MeVfm
=-320 MeVfm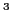 was slightly enlarged
to prevent pairing from
collapsing in the
was slightly enlarged
to prevent pairing from
collapsing in the 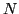 =99 system.
The resulting neutron pairing gaps,
=99 system.
The resulting neutron pairing gaps,
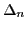 =1.2MeV and 0.77MeV in
=1.2MeV and 0.77MeV in 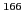 Er and
Er and 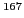 Er,
respectively, are reasonably close to the experimental values of 1.02MeV
and 0.62MeV.
Er,
respectively, are reasonably close to the experimental values of 1.02MeV
and 0.62MeV.
Figure 4 displays the quasiparticle spectrum for
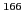 Er (top) and
Er (top) and 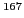 Er (bottom).
Er (bottom).
Figure 4:
(Color online)
One-quasiparticle levels of both signatures
(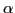 =1/2: solid line;
=1/2: solid line; 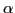 =-1/2: dotted line)
as functions of
=-1/2: dotted line)
as functions of 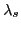 for
for 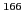 Er (top) and
Er (top) and 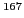 Er (bottom).
The levels occupied in the vacuum configuration are drawn by thick lines.
The calculations were carried out with a SLy4 Skyrme functional and mixed pairing.
See text for details.
Er (bottom).
The levels occupied in the vacuum configuration are drawn by thick lines.
The calculations were carried out with a SLy4 Skyrme functional and mixed pairing.
See text for details.
|
|
At the value of 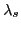 indicated by a star symbol, a transition
from a zero-quasiparticle vacuum corresponding to
indicated by a star symbol, a transition
from a zero-quasiparticle vacuum corresponding to 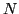 =98 to a one-quasiparticle
vacuum associated with
=98 to a one-quasiparticle
vacuum associated with 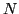 =99 takes place. As in the atomic case,
the mean-field
changes abruptly at the crossing point. Actually,
since the quasiparticle spectrum changes when going from
=99 takes place. As in the atomic case,
the mean-field
changes abruptly at the crossing point. Actually,
since the quasiparticle spectrum changes when going from
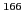 Er to
Er to 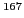 Er (both in terms of excitation
energy and ordering
of levels), the crossing point is shifted towards the lower values
of
Er (both in terms of excitation
energy and ordering
of levels), the crossing point is shifted towards the lower values
of 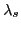 . As checked numerically, the result of calculations
for
. As checked numerically, the result of calculations
for  Er by explicitly blocking the
level ``a" are equivalent to those
with 2FLA carried out above the crossing point.
Er by explicitly blocking the
level ``a" are equivalent to those
with 2FLA carried out above the crossing point.



Next: Conclusions
Up: Hartree-Fock-Bogoliubov Theory of Polarized
Previous: Particle-number parity of the
Jacek Dobaczewski
2009-04-13
![]() =30 and 31 fermions
in a spherical (
=30 and 31 fermions
in a spherical (![]() =0) and deformed (
=0) and deformed (![]() =0.2) trap.
The HFB equations were solved by using the recently developed
axial DFT solver HFB-AX [35].
The results are displayed in Fig. 3.
=0.2) trap.
The HFB equations were solved by using the recently developed
axial DFT solver HFB-AX [35].
The results are displayed in Fig. 3.
![\includegraphics[trim=0cm 0cm 0cm 0cm,width=0.49\textwidth,clip]{fig3.eps}](img169.png)
![]() . However, as discussed in Sec. 3.2, the orbital
. However, as discussed in Sec. 3.2, the orbital
![]() +1)-fold degeneracy is present. Consequently, after the crossing
point, the vacuum becomes a
+1)-fold degeneracy is present. Consequently, after the crossing
point, the vacuum becomes a ![]() +1)-quasiparticle state, where
+1)-quasiparticle state, where
![]() is the orbital angular momentum of the lowest quasiparticle level.
For
is the orbital angular momentum of the lowest quasiparticle level.
For ![]() =30, the lowest quasiparticle excitation is a
=30, the lowest quasiparticle excitation is a ![]() state, i.e.,
above the crossing point the local HFB vacuum becomes a three-quaspiarticle
state.
At the crossing point, the self-consistent mean-field
changes abruptly. In particular,
the chemical potential
moves up as the number of particles increases by one,
and the pairing gap decreases due to blocking.
This produces a sharp discontinuity around the crossing point, which can be seen
in all three cases presented in Fig. 3.
state, i.e.,
above the crossing point the local HFB vacuum becomes a three-quaspiarticle
state.
At the crossing point, the self-consistent mean-field
changes abruptly. In particular,
the chemical potential
moves up as the number of particles increases by one,
and the pairing gap decreases due to blocking.
This produces a sharp discontinuity around the crossing point, which can be seen
in all three cases presented in Fig. 3.
![]() onto the symmetry axis of the trapping potential (
onto the symmetry axis of the trapping potential (![]() -axis).
Because of the Kramers degeneracy, levels with
-axis).
Because of the Kramers degeneracy, levels with ![]() are degenerate.
That is, except for
are degenerate.
That is, except for ![]() =0, each quasiparticle state is two-fold
degenerate. In the case presented in Fig. 3, the two lowest levels have
=0, each quasiparticle state is two-fold
degenerate. In the case presented in Fig. 3, the two lowest levels have
![]() =0, hence they are associated with one-quasiparticle excitations. The third
state has
=0, hence they are associated with one-quasiparticle excitations. The third
state has ![]() =1, and its crossing does not change
the particle-number parity of the HFB vacuum.
=1, and its crossing does not change
the particle-number parity of the HFB vacuum.
![]() Er (
Er (![]() =98) and
=98) and ![]() Er (
Er (![]() =99). The
pairing strength
=99). The
pairing strength ![]() =-320 MeVfm
=-320 MeVfm![]() was slightly enlarged
to prevent pairing from
collapsing in the
was slightly enlarged
to prevent pairing from
collapsing in the ![]() =99 system.
The resulting neutron pairing gaps,
=99 system.
The resulting neutron pairing gaps,
![]() =1.2MeV and 0.77MeV in
=1.2MeV and 0.77MeV in ![]() Er and
Er and ![]() Er,
respectively, are reasonably close to the experimental values of 1.02MeV
and 0.62MeV.
Er,
respectively, are reasonably close to the experimental values of 1.02MeV
and 0.62MeV.
![]() Er (top) and
Er (top) and ![]() Er (bottom).
Er (bottom).
![\includegraphics[trim=0cm 0cm 0cm 0cm,width=0.4\textwidth,clip]{fig4.eps}](img183.png)