Podstawy Julii

W tej części przedstawione są absolutne podstawy, takie jak składnia, definiowanie zmiennych prostych i złożonych czy funkcji. Dokładne czytanie po kolei tego rozdziału może być nudne - lepiej traktować go jako zebranie najważniejszych informacji w jednym miejscu, do którego można odwoływać się w razie potrzeby doczytania o jakimś zagadnieniu.

  1. Zmienne
  2. Liczby
  3. Operatory matematyczne
  4. Operatory logiczne
  5. Operatory bitowe
  6. Operatory "z kropką"
  7. Porównania liczb
  8. Rzutowanie typów
  9. Funkcje matematyczne
  10. Ciągi znaków
  11. Instrukcje kontrolne
    1. if elseif else
    2. Pętla while
    3. Pętla for
    4. try-catch
  12. Typy
    1. Unia
    2. Typy złożone
    3. Typy parametryczne
    4. Typy abstrakcyjne
  13. Funkcje
    1. Wiele zwracanych wartości
    2. Wartości domyślne
    3. Argumenty nazwane
    4. Siorbanie i plaśkanie
    5. Funkcje anonimowe
    6. Metody
  14. Krotki (tuple)
  15. Słowniki
  16. Macierze
  17. Tworzenie macierzy
    1. Typowe operacje
  18. Rozszerzenia
  19. Pomiar szybkości
    1. Przykład
  20. Menadżer pakietów
  21. Środowiska

Zmienne

x = 1
x + 1
x = 1 + 1
println("x = ", x)
x = "Hello World!"

Nazwy zmiennych są wrażliwe na wielkość liter i mogą używać kodowania UTF-8. Muszą zaczynać się od litery, podkreślenia lub znaku Unicode o numerze większym niż 00A0. W odpowiednio skonfigurowanym edytorze można wprowadzać znaki przez nazwy podobne jak w LaTeX-u i tabulator (np. \alpha+<TAB>).

∫₀(x) = x

Zadanie:

Zapisać wzór na masę zredukowaną w Julii korzystając ze znaków Unicode

μ=m1m2m1+m2 \mu = \frac{ {m}_{1} {m}_{2} }{ {m}_{1} + {m}_{2} } 
μ = m₁ * m₂ / (m₁ + m₂)

Liczby

Wbudowane typy liczbowe obejmują liczby całkowite i zmiennoprzecinkowe, o różnej dokładności (Int8-Int128, Float16-Float64). Tworząc zmienną bez deklaracji typu, powierzamy jego identyfikacje automatowi

x = UInt32(1)
typeof(x)
x = 1.0
typeof(x)
x = 0xF1
typeof(x)
x = 0x0001
typeof(x)
x = 0b01010101000
typeof(x)
x = 0o010
typeof(x)

Maksymalną i minimalną liczbę całkowitą danej reprezentacji można uzyskać przez typemin(T) i typemax(T). Funkcja bitstring() zwraca reprezentację bitową w postaci ciągu znaków

typemax(Int64)
bitstring(typemin(Float64))

Liczby zmiennoprzecinkowe są 64 (domyślnie) lub 32 bitowe

x = 1.0
typeof(x)
x = 1.0e-5
typeof(x)
x = 1.0f-5
typeof(x)

Zadanie Sprawdzić działanie funkcji eps(), nextfloat(), prevfloat() i reprezentacji bitowej uzyskanych wyników

bitstring(1.0e15)
nextfloat(1.0e15)
eps(1.0)
#a1.0e15 + 0.0125

Operatory matematyczne

  • x + y

  • x - y

  • x * y

  • x / y

  • x ÷ y (\div+<TAB>, lub div(x, y))

  • x % y

  • x^y

  • oraz odpowiednie +=, -=, *=, ...

Zadanie: Sprawdzić działanie operatorów na zmiennych typu Int i Float, oraz typ otrzymanego wyniku

's'^2

Operatory logiczne

  • !x

  • x || y (lub) - y jest sprawdzane tylko jeżeli x jest fałszywe

  • x && y (i) - y jest sprawdzane tylko jeżeli x jest prawdziwe

x = -2
sqrt(x)

Operatory bitowe

  • ~x (negacja)

  • x & y (i)

  • x | y (lub)

  • x ⊻ y (albo = xor(x, y))

  • x >>> y (przesunięcie logiczne - nie zachowuje bitu znaku)

  • x >> y (przesunięcie arytmetyczne - zachowuje bit znaku)

Zadanie: Sprawdzić działanie przesunięc w prawo dla x = Int8(-64)

x = Int8(-64)
println(bitstring(x))
println(bitstring(x >> 1))
println(bitstring(x >>> 1))

Operatory "z kropką"

Dla każdego operatora binarnego (+, -, ...) jest zdefiniowany operator z kropką (.+, .-, ...), który działa na macierzach powtarzając operację dla każdego elementu. Podobna składnia obowiązuje funkcje (np. sin.(x)), natomiast makro @. przerabia każdy operator i funkcję na wersję z kropką.

x = [1, 2, 3]
println(x .^ 2)
println(sin.(x))
@. sqrt(sin(x) + 2x + 1)

Porównania liczb

Liczby i zmienne można porównywać typowymi operatorami (==, !=, >=, <=). Operatory można łączyć w łańcuchy (jak w Pythonie), np. 0 <= x < 1

x = 0.5
0 <= x < 1

Operatory porównują wyrażenia zgodnie ze standardem IEEE754 - w szczególnych przypadkach (NaN, Inf) prowadzi to do zaskakujących wyników

println(NaN == NaN)
println(NaN < NaN)
println(NaN > NaN)
println(Inf == Inf)
println(Inf > Inf)
println(Inf > NaN)
println(-0.0 == 0.0)
println(bitstring(-0.0))
println(bitstring(0.0))

W pewnych sytuacjach mogą pomóc specjalne funkcje isequal(), isfinite(), isnan(), isinf()

println(isequal(NaN, NaN))
println(isequal(-0.0, 0.0))

Kolejność operatorów

  • ^

  • √

  • << >> >>>

    • / %

      • | & ⊻

  • : .. (składnia: range, )

  • |> (pipe)

  • <|

  • < > == >= != ...

  • && || ?

  • => (para)

  • = += -= *= ...

Zadanie: Sprawdzić następujące wyrażenia

  • 1 == 3 & 1 == 1

  • 1:2 .+ 3

(1 == 3) & (1 == 1)
(1:2).+3

Rzutowanie typów

  • T(x) (gdzie T to typ np. Float64, Int64, ...)

  • convert(T, x)

  • round(x)

  • round(T, x)

  • round(T, x, digits=n)

  • ceil/floor/trunc (x), (T, x)

Zadanie: Sprawdzić działanie powyższych funkcji dla różnych konwersji (Int - Float)

round(Int64, 1.5)

Funkcje matematyczne

  • div

  • fld

  • cld

  • mod

  • abs

  • abs2

  • sign

  • sqrt

  • cbrt

  • exp

  • log

  • log10

  • log(b, x)

  • sin

  • cos

  • tan

  • asin

  • acos

  • atan

  • isone

  • iszero

stałe

  • pi, \pi+<TAB>

  • \euler+<TAB>

log(ℯ)

Ciągi znaków

Typ Char reprezentuje pojedynczy znak (32-bitowa zmienna). Znak powinien być objęty cudzysłowem '. Wartości z tablic Unicode można wpisać korzystając z \u (liczba hex 4 cyfry) lub \U (liczba hex 8 cyfr)

c = 'x'
println(typeof(c))
println(Int64(c))
println(Char(120))
println('\u2200')

Ciągi znaków (String) są definiowane przez cudzysłów ", lub trzy cudzysłowy """. Mogą zawierać znaki Unicode (co powoduje pewne problemy pokazane poniżej. Ze względu na różną liczbę bitów kodującą znaki, indeks ostatniego znaku nie koniecznie jest długością ciągu. Indeksowanie elementów (tak jak i w innych strukturach) zaczyna się od 1.

s = "Hello world!\n"
println(s)
println(s[1], " ", s[end-1], " ", s[1:3])
s2 = "α² + β² = \u03DE²"
println(s2)
#println(s2[1], " ", s2[2])
println(collect(eachindex(s)))
println(collect(eachindex(s2)))

Sklejanie ciągów (concatenation) dokonujemy operatorem * (matematyczna idea jest taka, że + jest operatorem komutującym, a * niekoniecznie, sklejanie nie jest komutującą operacją).

"Ala " * "ma " * "kota."

Interpolacja to wstawianie zmiennych lub wyrażeń do ciągu znaków w miejscu oznaczonym znakiem $ (jak w bashu). W związku z tym ten znak traktowany dosłownie musi być wstawiany jako \$.

println("$")
s = "2 + 2 = $(2 + 2)"
x = 3.14159
println("π ≈ $x")
v = [1, 2, 3]
println("v = $v")
howmuch = 100.0
println("Jesteś mi winny \$$howmuch")

Instrukcje kontrolne

if elseif else

x = 0
if x > 0
    println(">0")
elseif x < 0
    println("<0")
else
    println("=0")
end

Instrukcja if musi mieć podaną zmienną typu Bool, w odróżnieniu od C, Pythona i wielu innych języków nie można użyć jej w następujący sposób 

if 1
    println("TAK")
end

Pętla while

x = 1
while x <=5 
    println(x)
    x += 1
end

W pętlach działają typowe polecenia continue i break

Pętla for

Pętla for zasadniczo iteruje po jakiejś kolekcji (macierzy, łańcuchu, zakresie, zbiorze,...). Zamiast słowa in można użyć \in+<TAB> lub =.

for i in 1:5
    println(i)
end

Składnia 1:5 daje tzw. zakres (range), specjalny typ zdefiniowany przez 3 liczby: początek, krok i koniec. W odróżnieniu od np. Pythona koniec jest zawarty.

typeof(1:5)

Krok jest definiowany przez środkową liczbę.

for i in 1:0.1:2
    println(i)
end
typeof(1:0.1:2)

Zamiast tej składni można użyć funkcji range(start, stop; length, step) podająć dwie z start, stop, length lub trzy wielkości ze wszystkich (pozostałe zostaną wyliczone automatycznie).

for i in range(stop=0, step=0.2, length=5)
    println(i)
end
for i in [3, 5, 8]
    println(i)
end

for i ∈ "ABC"
    println(i)
end

for i = [3, 5, 7]
    println(i)
end

Ciekawostką jest skrócony zapis zagnieżdżonych pętli

for i in 1:3, j in i:3
    println(i, " ", j)
end

Podobnie jak w Pythonie istnieje też funkcja zip sklejącą kolekcje

for (i, j) in zip(1:3, 4:10)
    println(i, " ", j)
end

try-catch

Również podobnie jak w innych językach działa pętla try-catch obsługująca wyjątki. Po złapaniu wyjątku można go obsłużyć sprawdziając jego typ funkcją isa(). W przypadku konieczności wyrzucenia wyjątku posługujemy się funkcją throw(), np. throw(DomainError(x, "x musi być większy od zera")).

s = begin
    #x = 2
    x = -2 + 0im
    try
        sqrt(x[2])
    catch err
        if isa(err, DomainError)
            println("DE")
            sqrt(complex(x[2], 0))
        elseif isa(err, BoundsError)
            println("BE")
            sqrt(x)
        end
    end
end

println(s)

Typy

Julia posiada system typów dynamiczny. Każdy typ należy do drzewa typów. Zmienne nie muszą mieć deklarowanych typów (wtedy zostanie im nadany automatycznie), ale mogą, jeżeli jest to potrzebne do wydajności, czytelności lub użycia "multiple dispatch".

Typy występują w trzech odmianach:

  • abstrakcyjne (definują strukturę drzewa typów)

  • typy konkretne (nie ma sensu dodawać nowych)

  • unie typów (abstrakcyjne)

  • typy złożone (struktury)

  • typy parametryczne (odpowiednik templatów)

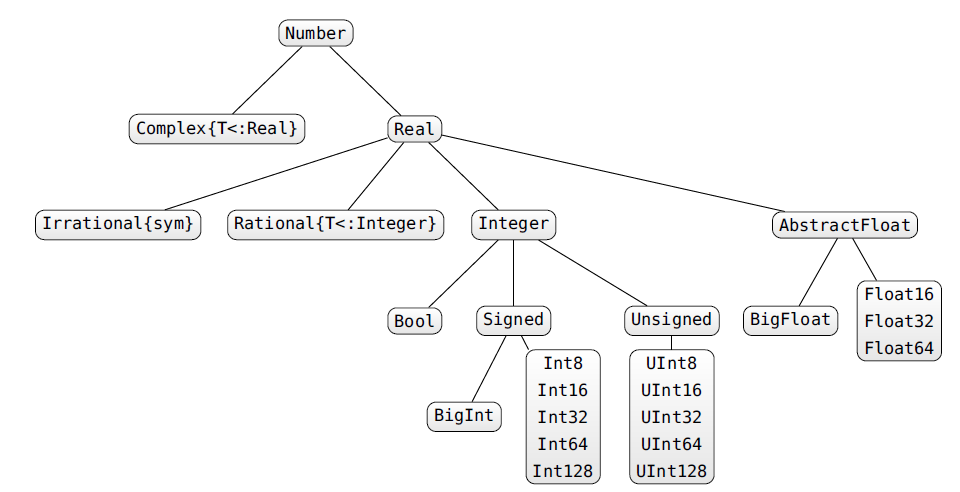
vWAiB.png

Operator <: (oznaczający "jest podtypem") może być używany do tworzenia nowego typu, albo zwraca prawdę/fałsz w wyrażeniach testujących hierachię typów

println(Int64 <: Real)
println(Float64 <: Signed)

Unia

Unia typów to abstrakcyjny typ zawierający wszystkie wymienione typy Union{Int64, Float64}. Przy analizie wydajności zwykle oznacza to niestabilność typową funkcji, co daje wolniejszy kod.

Typy złożone

Typy złożone to struktury lub obiekty składające się z nazwanych pól. W odróżnieniu od języków obiektowych struktury w Julii nie zawierają funkcji, które aby korzystać z mechanizmów multiple dispatch żyją na zewnątrz struktur.

Nowy obiekt jest tworzony po wywołaniu struktury pod postacią funkcji (konstruktor). Dostęp do pól jest przez notację z kropką (A.a).

struct Point
    x::Float64
    y::Float64
    name::String
end

p0 = Point(0.0, 0.0, "origin")
println(p0, " ", typeof(p0))
println(p0.x)

Tak zadeklarowane obiekty są niezmienne. Dzięki temu mogą być kopiowane przez kompilator (są nierozróżnialne) i lokowane na stosie (stack). 

p0.x = 1.0

Struktura zmienna jest deklarowana przez mutable struct. Ten typ nie może być z góry roztrzygnięty przez kompilator. Jest umieszczany na stercie (heap).

mutable struct PointM
    x::Float64
    y::Float64
    name
end

p1 = PointM(0.0, 0.0, "M")
println(p1, " ", typeof(p1.name))
p1.name = 1.0
println(typeof(p1.name))

Typy parametryczne

Typ parametryczny (zwyczajowo oznaczony jako T) jest odpowiednikiem konternerów w C++. Dzięki temu można tworzyć ogólne elastyczne struktury, których konkretne realizacje zależą od końcowego typu.

struct PointP{T}
    x::T
    y::T
end

p0 = PointP{Int64}(0, 0)
p1 = PointP{Float64}(0.0, 0.0)
println(typeof(p0))
println(typeof(p1))

Zakres i typ T można zawęzić poprzez operator <:

struct PointR{T <: Real}
    x::T
    y::T
end

p0 = PointR{String}("A", "B")

Typy abstrakcyjne

Służą do definiowania drzewa typów. W poniższym przykładzie abstrakcyjny typ Curve ma podtypy Circle, Line. Z kolei struktura Region zawiera macierz obiektów typu Surface, a więc mogą być to zarówno linie, jak i okręgi.

abstract type Curve end

struct Line <: Curve
    x1::Float64
    y1::Float64
    x2::Float64
    y2::Float64
end

struct Sphere <: Curve
    x0::Float64
    y0::Float64
    R::Float64
end

struct Region
    curves::Array{Curve, 1}
    operators::Array{Bool, 1}
end

function isin(x, y, c::Line)
    
end

function isin(x, c::Sphere)
    
end

function isin(x, y, r::Region)
    
end

l1 = Line(0.0, 0.0, 0.0, 1.0)
s1 = Sphere(0.0, 0.0, 1.0)

r1 = Region([l1, s1], [true, true])
println(r1)

Funkcje

Funkcje w Julii nie są czysto matematycznymi funkcjami, ponieważ w ogólności mogą modyfikować argumenty. Jeżeli funkcja zachowuje się w ten sposób to oznacza się ją zwyczajowo wykrzyknikiem, np

sort(x)
sort!(x)

są dwiema wersjami sortowania, sort(x) zwraca nowy wektor, a sort!(x) sortuje w miejscu (więc modyfikuje argument).

Składnia:

function f1(x, y)
    return 2x + y
end

Δ(x, y) = abs(x - y)

Słowo return oznacza oczywiście zwrócenie wartości i wyjście z funkcji w miejscu wywowałnia. Jeżeli go nie użyjemy funkcja zwróci ostatnią wykonaną operację

Funkcje są takimi samymi obiekatami jak zmienne, więc również można je np. przekazywać

function f2(x, y)
    return 2x + y
print("C")
end

println(f2(1, 1))

Funkcje są takimi samymi obiekatami jak zmienne, więc również można je np. przekazywać

function d(f, x)
    return f(x, x)
end

k = d
println(k(f1, 2))
println(k(Δ, 2))

Deklaracja typów nie wpływa na wydajość, ale może służyć rozróżnianiu wersji funkcji

function f(x::Int64, y::Int64)
    return 2(x + y)
end

function f(x::Float64, y::Float64)
    return √2(x + y)
end

println(f(1, 1))
println(f(1.0, 1.0))

Podobnie można zadeklarować typ zwracanej wartości, ale jest to rzadko używane (lepiej pisać kod stabilny typowo i zostawić roztrzygnięcie kompilatorowi).

function fi(x, y)::Int64
   x + y
end

println(fi(1, 1))
@code_native fi(1, 1)
println(fi(1.0, 1.0), " ", typeof(fi(1.0, 1.0)))
@code_native fi(1.0, 1.0)

Zadanie Na podstawie publikacji C. Lanczosa napisać funkcję wyznaczająca wartość funkcji Gamma.

Wiele zwracanych wartości

Funkcja może zwracać wiele wartości jednocześnie

function m(x, y)
    return x + y, x - y
end

a, b = m(1, 1)
println(a, " ", b)

Wartości domyślne

Funkcja może mieć zdefiniowane domyślne wartości. Przy wywoływaniu można te argumenty pominąć. Muszą one być podane na końcu definicji.

function p(x, y::Int64=1)
    return x^y
end

println(p(2))
println(p(2, 2))

Argumenty nazwane

W definicji funkcji argumenty zebrane po średniku będą argumentami nazwanymi, zwykle mają one zdefiniowane też wartości domyślne. Taka składnia umożliwia podawanie dowolnej liczby nazwanych argumentów w dowolnej kolejności i jest przydatane do funkcji, w której potrzebne jest ich dużo i trudnoby było zapamiętać i stosować odpowiednią kolejność.

function potential(x; a=0.5, V0=-50.0, r0=1.25, k=1.0, m0=939.494)
    ###
end

potential(1.0)
potential(1.0; V0=-45.0, a=0.1)

Siorbanie i plaśkanie

W definicji funkcji operator ... zbiera wiele argumentów do jednego ("siorbie" - slurping), umożliwiając ich elastyczne przekazywanie. Tak samo przy zwracaniu wartości z funkcji lub z elementu złożonego możemy ich kilka połączyć w jeden.

function f(a, b, c...)
    return a * b .+ c
end
println(f(1, 2, 3, 4, 5))
a, b... = "hello"
println(a, " ", b)

Jeżeli w definicji funkcji użyjemy średnika, oddzielającego nazwane argumenty i połączymy je z siorbaniem, efektem będzie zebranie argumentów w pary klucz=>wartość.

function g(;args...)
    println(args)
end
println(g(a=1, b=0.0, c="A"))

Jednocześnie ten sam operator użyty w kontekście wywołania funkcji, działa w drugą stronę i "rozplaśkuje" (splatting) argument złożony, np. tablicę, na pojedyncze argumenty

function h(x, a1, a2, a3)
    a1 + a2 * x + a3 * x^2
end

p = [1, 0, 1]
h(2, p...)

Funkcje anonimowe

Funkcje anonimowe (lambda) to funkcje bez nazwy, typowo przekazywane do innych funkcji. Klasycznym przykładem jest przekazanie funkcji anonimowej do funkcji map, która wykonuje ją potem na każdym elemencie kolekcji. Składnia funkcji anomimowej używa strzałki -> np.

x -> x^2 + 1 
println(map(round, [1.43, 1.51, 1.67]))

Takie wywołanie działa jeżeli chcemy użyć istniejącej funkcji. Ale jeżeli chcemy zaokrąglenia z zadaną dokładnością lub zupełnie innej operacji możemy użyć funkcji anonimowej.

println(map(x->round(x, digits=1), [1.43, 1.51, 1.67]))
println(map(x->sqrt(x + 1), [1.43, 1.51, 1.67]))

Metody

Większość operatorów w Julii jest także funkcjami. Np. + jest funkcją +(x, y).

Każda funkcja może mieć różne wersje, w zależności od typów argumentów. O dostępne metody możemy się zapytać polecieniem methods.

methods(f)
methods(+)

Krotki (tuple)

Krotki to niezmiennicze kolekcje deklarowane przez nawiasy okrągłe (). Krotki nazwane są bardzo podobne, oprócz tego, że argumenty mają przypisane nazwy i można się do nich odnosić przez notację z kropką.

k = (3, 5, 8)
println(k[1])
k = (a=3, b=5, c=8)
println(k[2], " ", k.b)

Słowniki

Słowniki to standardowa struktra zbudowana na zasadzie par klucz-wartość. Klucze i wartości mogą mieć różne typy. Najprostszym sposobem stworzenia słownika jest wymienienie elementów i powiązanie ich w pary operatorem =>.

d = Dict("A" => 1, "B" => 2)

Jak widać typ został nadany automatycznie. Możemy go także podać podczas tworzenia bezpośrednio. Poniżej pusty słownik String, Any (czyli przechowujący dowolne elementy)

d = Dict{String, Any}()
d["A"] = 1
d["B"] = "b"
d["C"] = [1, 2, 3]
println(d)

Przypisanie d["A"] tworzy nowy element lub zmienia istniejący. Odwołanie się do nieistenijącego elementu powoduje wyrzucenie błędu. Aby sprawdzić czy dany klucz jest w słowniku można użyć funkcji haskey. Funkcja keys zwraca wszystkie klucze, values - wartości, pairs - pary.

println(haskey(d, "D"))
for (k, v) in pairs(d)
    println(k, " ", v)
end

Macierze

Macierz to kolekcja elementów przechowywana na wielowymiarowej siatce. Bazowym typem dla wszystkich macierzy jest AbstractArray. Wszystkie macierze są przekazywane do funkcji przez dzielenie się (np. za pomocą wskaźników). Oznacza to, że jeżeli funkcja modyfikuje macierz (kończy się na !), a chcemy zachować oryginał, musimy wykonać kopię.

Tworzenie macierzy

Macierze są tworzone przez kilka różnych składni

  1. Bezpośrednie podanie elementów

A = [1, 2, 3]
A = [1 2 3]

Jak widać w Julii istnieje różnica pomiędzy wektorami (macierzami kolumnowymi), a macierzami poziomymi!

Wielowymiarowe macierze tworzymy przez użycie nowych linii lub średników (elementy są łączone werykalnie). Podwójny średnik łączy horyzontalnie.

A = [1 2 3
    4 5 6]
A = [1 2 3; 4 5 6]
A = [[1, 2] [3, 4] [5, 6]]
A = [[1, 2], [3, 4], [5, 6]]

Możemy również użyć zasięgów

A = [1:4 9:12]
A = [1:4, 9:12]
A = [1:4; 9:12]
A = [1:4;; 9:12]

  1. Typowe macierze można tworzyć specjalnymi funkcjami

A = zeros(2, 3)
A = zeros(Int64, 2, 3)
A = ones(2, 3)
A = rand(2, 3)
A = randn(2, 3)

  1. Podobnie jak np. w Pythonie macierze i inne kolekcje można tworzyć także za pomocą generatorów

A = [i for i in 1:10]

  1. Niezainicjowana macierz

A = Array{Float64}(undef, 3, 3)

  1. Pusta macierz

A = Array{Float64, 1}()
A = Array{Float64}(undef, 0, 0)

Typowe operacje

A = [1 2 3; 4 5 6]
length(A)
size(A)
reshape(A, 3, 2)
reinterpret(Float64, A)
B = A
C = copy(A)
fill!(B, 0)
fill!(C, 1)
@show A 
@show B
@show C
x = [0, 1, 2]
push!(x, 3)
append!(x, [4, 5, 6])
prepend!(x, -1)

Rozszerzenia

Rozszerzenia w Julia są w postaci pakietów. Dokładniejszą ich budową zajmiemy się później. W tym miejscu potrzebne nam będą polecenia importujące moduły: using i import.

using - ładuje kod modułu oraz jego nazwę i wyeksportowane elementy do globalnej przestrzeni nazw

import - ładuje kod modułu oraz tylko jego nazwę do globalnej przestrzeni nazw

W Pythonie byłby to odpowiednik from X import * (using) oraz import X (import).

import LinearAlgebra

A = Matrix{Float64}(LinearAlgebra.I, 2, 2)
using LinearAlgebra

B = Matrix{Float64}(I, 2, 2)
?det

Zadanie: Do pokazanych wcześniej struktur Region napisać funkcję zwracającą prawdę jeżeli przekazany punkt jest wewnątrz regionu i fałsz jeżeli na zewnątrz. Region jest zdefiniowany przez krzywe i operatory (prawda/fałsz), które decydują czy jest on wewnątrz czy na zewnątrz danej krzywej.

W przypadku prostej dany punkt jest wewnątrz jeżeli wyznacznik macierzy det⁡∣AB∣\det\left|A B\right| jest dodatni (zakładamy, że punkt na krzywej nie jest wewnątrz), gdzie A⃗=x2⃗−x1⃗,B⃗=x⃗−x1⃗\vec{A} = \vec{x_2} - \vec{x_1}, \vec{B} = \vec{x} - \vec{x_1}, gdzie x1⃗,x2⃗\vec{x_1}, \vec{x_2} to punkty definujące prostą, x⃗\vec{x} punkt o który pytamy.

Pomiar szybkości

Ponieważ wydajność jest jedną z kluczowych założeń Julii, staramy się, aby kod był możliwie szybki. Aby ocenić jego jakość musimy mieć jakieś narzędzia.

Najprostszą metodą jest makro @time, @timev i @elapsed

function simplesum(N)
    s = 0
    for i in 1:N
        s +=i 
    end
    s
end

println("simplesum time")
@time simplesum(10000000)
println("sum time")
@time sum(1:1000000)
println("simplesum timev")
@timev simplesum(1000000)
println("sum timev")
@timev sum(1:1000000)
println("simplesum elapsed")
@elapsed simplesum(1000000)
println("sum elapsed")
@elapsed sum(1:1000000)

Te metody pozwalają ocenić prędkość, ale nie są statystycznie wiarygodne, bo mogą zawierać czas kompilacji, a pojedyncza próba może nie być reprezentacyjna.

Moduł BenchmarkTools dostarcza bardziej wiarygodnych narzędzi @btime i @benchmark, które wskazują także na użycie pamięci.

using BenchmarkTools

@btime simplesum(10000000)
@benchmark simplesum(1000000)

Jeszcze bardziej szczegółowych informacji można uzyskać korzystając z profilera (moduł Profile).

using Profile
@profile simplesum(1000000)

Profile.print()
using ProfileView
@profile sum(1:1000000)
ProfileView.view()

Przykład

Rozważmy następujący problem: chcemy znaleźć indeks najmniejszego elementu w danej tablicy. Jeżeli taki sam wyraz występuje więcej niż jeden raz, chcemy dostać losowy element (z równym prawdopodobieństwem).

Julia nie posiada wbudowanej procedury tego typu. Możemy natomiast użyć kilku wbudowanych funkcji (minimum, filter, rand oraz eachindex), aby osiągnąc pożądany rezultat.

function randminarg1(a)
    m = minimum(a)
    rand(filter(i -> a[i] == m, eachindex(a)))
end

x = [1, 2, 3, 1, 1, 3]
randminarg1(x)

Logika jest tu prosta:

  • szukamy najmniejszego elementu (minimum)

  • dla każdego indeksu (eachindex tworzy wydajny iterator chodzący po kolekcjach) sprawdź, czy element jest równy najmniejszemu

  • zwróć losowy element (rand) listy indeksów

Sprawdzimy działanie funkcji na większej próbce

using StatsBase

countmap([randminarg1(x) for i in 1:10000])

countmap z modułu StatsBase zwraca mapę (słownik) unikatowych wyrażeń występujących w kolekcji oraz liczbę ich wystąpień.

Algorytm, który tu zastosowaliśmy musi przeglądać tablicę dwa razy. Czy jest to najlepszy sposób? Okazuje się, że można zrobić to w jednym przejściu tablicy:

  • Jeżeli spotkasz nową najmniejszą wartość to ją zapamiętaj minval i jej indeks imin

  • Jeżeli ta wartość została już spotkana b razy, to imin powinien przechowywać indeks każdej z nich z prawdopodobieństwem 1/b1/b.

  • Jeżeli spotkamy nowe miejsce jej występowania to z prawdopodobieństwem 1/(b+1)1/(b+1) powinniśmy go przechować. Wtedy każdy z poprzednich wyrazów będzie miał prawdopodobieństwo przechowywania:

1b×(1−1b+1)=1bbb+1=1b+1 \frac{1}{b} \times (1 - \frac{1}{b + 1}) = \frac{1}{b}\frac{b}{b+1} = \frac{1}{b+1}

Nasz algorytm, podobnie jak powyższy powienien działać dla dowolnych kolekcji (nie tylko jednowymiarowego wektora). Dlatego użyjemy iteratora poruszającego się po kolekcji indeksów. iterate() zwraca krotkę zawierającą dwie wartości - kolejny (lub pierwszy) element kolekcji oraz stan (który można podawać do następnych iteracji. Jeżeli kolekcja się skończy, funkcja zwróci nothing.

function randminarg2(a)
    indices = eachindex(a)
    y = iterate(indices)
    y == nothing && throw(ArgumentError("collection must be non-empty"))
    (idx, state) = y
    minval = a[idx]
    bestidx = idx
    bestcount = 1
    y = iterate(indices, state)
    while y !== nothing
        (idx, state) = y
        current = a[idx]
        if isless(current, minval)
            minval = current
            bestidx = idx
            bestcount = 1
        elseif isequal(current, minval)
            bestcount += 1
            rand() * bestcount < 1 && (bestidx = idx)
        end
        y = iterate(indices, state)
    end
    bestidx
end

Sprawdzamy działanie

countmap([randminarg2(x) for i in 1:10000])

Wreszcie przetestujemy wydajność jednego i drugiego podejścia

using BenchmarkTools

x = rand(1:2, 1_000_000)
@benchmark randminarg1($x)
@benchmark randminarg2($x)

Dla większych rozmiarów tablic randminarg2 jest wolniejsze niż randminarg1! Proszę sprawdzić profilerem dlaczego!

@profile randminarg2(rand(1:10, 1000000))
Profile.print()
ProfileView.view()

Zadanie: Napisać funkcję sumującą wyrazy dwuwymiarowej macierzy w wersji iterującej najpierw po wierszach i najpierw po kolumnach. Sprawdzić prędkość dla losowych macierzy 10^4x10^4. Zoptymalizować znalezione problemy i porównać czas z wbudowaną funkcją sum.

A = rand(3, 3)
sum(A)
function sum1(A)
    sz = size(A)
    s = zero(eltype(A))
    for i in 1:sz[1]
        for j in 1:sz[2]
            s += A[i, j]
        end
    end
    s
end
A = rand(10^4, 10^4)
#@code_warntype sum1(A)
@benchmark sum1($A)
function sum2(A)
    sz = size(A)
    s = zero(eltype(A))
    for j in 1:sz[2]
        for i in 1:sz[1]
            s += A[i, j]
        end
    end
    s
end
A = rand(10^4, 10^4)
@benchmark sum2($A)
A = rand(10^4, 10^4)
@benchmark sum($A)

Menadżer pakietów

Do tej pory zdążyliśmy użyć już kilku dodatkowych pakietów (np. BenchmarkTools). Te, które nie należą do standardowej biblioteki muszą zostać zainstalowane. W REPL-u próba użycia pakietu, którego brakuje kończy się pytaniem o instalację i jest to najprostsza metoda.

Normalna, nie interaktywna instalacja, używa modułu Pkg z biblioteki standardowej. Pkg jest menadżerem pakietów w Julii, który po pierwsze instaluje i usuwa pakiety. Ale, co równie istotne, zarządza całym systemem niezależnych środowisk (environments) przypisanych do różnych projektów - o czym za chwilę.

Instalacja, aktualizacja czy usunięcie pakietu wygląda następująco

julia> using Pkg
julia> Pkg.add("Pakiet")
julia> Pkg.update("Pakiet")
julia> Pkg.rm("Pakiet")

Alternatywnie możemy przejść w REPL-u w tryb menadżera (]) i używać wersji

(@v1.11) pkg> add Pakiet
(@v1.11) pkg> update Pakiet
(@v1.11) pkg> rm Pakiet

Środowiska

W ostatnim przypadku przed znakiem zachęty (pkg>) widzimy tajemniczy napis @v1.11 lub podobny, który, co dość łatwo się domyślić, oznacza wersję zainstalowanej Julii. Jednocześnie jest to oznaczenie aktualnego środowiska, którym domyślnie jest główne środowisko. Julia posiada cały system środowisk. Nowe możemy utworzyć przez polecenie activate NazwaProjektu

(@v1.11) pkg> activate Projekt1
(Projekt1) pkg>

Jak widać znak zachęty zmienił się na (Projekt1). Od tej pory operacje instalacji dotyczą tylko aktywnego środowiska.

(Projekt1) pkg> add GLMakie

W tym momencie na dysku, w miejscu gdzie pracowaliśmy powinien pojawić się katalog Projekt1 zawierający pliki Project.toml i Manifest.toml. Te dwa pliki definiują po pierwsze jakie moduły chcemy mieć w projekcie (Project.toml) i jakie mamy w projekcie (Manifest.toml). Czym to się różni? Zajrzyjmy do plików.

Project.toml:

[deps]
GLMakie = "e9467ef8-e4e7-5192-8a1a-b1aee30e663a"
Manifest.toml

# This file is machine-generated - editing it directly is not advised

julia_version = "1.11.2"
manifest_format = "2.0"
project_hash = "507b61fec42f925d5a0331ff375389111e604512"

[[deps.AbstractFFTs]]
deps = ["LinearAlgebra"]
git-tree-sha1 = "d92ad398961a3ed262d8bf04a1a2b8340f915fef"
uuid = "621f4979-c628-5d54-868e-fcf4e3e8185c"
version = "1.5.0"
weakdeps = ["ChainRulesCore", "Test"]

    [deps.AbstractFFTs.extensions]
    AbstractFFTsChainRulesCoreExt = "ChainRulesCore"
    AbstractFFTsTestExt = "Test"

[[deps.AbstractTrees]]
git-tree-sha1 = "2d9c9a55f9c93e8887ad391fbae72f8ef55e1177"
uuid = "1520ce14-60c1-5f80-bbc7-55ef81b5835c"
version = "0.4.5"

(...)

Project.toml mówi, że chcieliśmy zainstalować bibliotekę GLMakie (do tworzenia wykresów). Manifest.toml podaje listę rzeczywiście zainstalowanych bibliotek, w tym tych, od których GLMakie zależy. W obu przypadkach dokładna wersja biblioteki (pakietu) jest identyfikowana przez uuid, kod zmiany w systemie kontroli wersji git. Wszystkie oficjalne moduły Julii są umieszczone, wraz z całą historią zmian, na serwerze github, więc możemy zawsze poprosić o dowolną wersję od samego początku utworzenia danego pakietu.

W ten sposób dochodzimy do pierwszej korzyści z korzystania ze środowisk. Jeżeli w dowolnym momencie chcemy odtworzyć nasz projekt i używać tych samych wersji bibliotek, których kiedyś używaliśmy, to umożliwiają to pliki Project i Manifest. Aktywując istniejące środowisko przenosimy się do stanu Julii w jakim była ona zapisana.

(@v1.11) pkg> activate MójStaryProjekt
Activating project at `~/MójStaryProjekt

(MójStaryProjekt) pkg> instantiate

Jakie biblioteki i w jakiej wersji zawiera środowisko możemy sprawdzić poleceniem status (lub st)

(MójStaryProjekt) pkg> status

Środowiska powinny po pierwsze wyeliminować zatem problem z aktualizacjami i zmianami w bibliotekach. Po drugie wysłanie komuś (lub otrzymanie od kogoś) kodu wraz ze środowiskiem (plikami Project i Manifest) powinno być wystarczające, aby działał on tak jak u autora - znany w wielu językach problem "u mnie działało" powinien także być rozwiązany.

Aby aktywować istniejące środowisko musimy znajdować się katalog wyżej ponad nazwą środowiska (np. jeżeli środowisko jest zapisane w /home/user/Projekt1, to możemy być w /home/user) lub jeżeli jesteśmy w katalogu środowiska (czyli /home/user/Projekt1) przez ] activate .. Trzecią metodą jest uruchomienie Julii z parametrem julia --project=Projekt1 i bezpośrednie załadowanie wskazanego środowiska (oczywiście musimy być w odpowiednim miejscu).

Środowiska w Julii mają jeszcze dwie cechy, które warto znać. Po pierwsze mogą być dzielone - mają wtedy symbol "@" przed nazwą. Dzielone środowisko może być aktywowane z dowolnego miejsca na komputerze, a nie tylko bezpośrednio z katalogu środowiska.

(@v1.11) pkg> activate @scratch

Szczególnym dzielonym środowiskiem jest środowisko główne (@v1.11 lub podobne z oznaczeniem wersji Julii).

Drugą cechą jest możliwość układania środowisk w stosy - jedne na drugich. Przy ładowaniu modułów w wewnętrznym środowisku, jeżeli nie są one tam dostępne, ładowane są one z kolejnego, bardziej zewnętrznego środowiska. Najbardziej zewnętrznym środowiskiem, wewnątrz którego są wszystkie inne, jest środowisko główne (@v1.11 itp.). Każdy moduł tam zainstalowany, może być ładowany w innych środowiskach. Teoretycznie wystarczy więc wszystkie potrzebne moduły instalować na tym poziomie.

Niestety wynikają z tego pewne problemy. Wyobraźmy sobie, że pracujemy w środowisku X, które potrzebuje modułu Y w wersji 2.0. Ale jakiś inny moduł, zainstalowany w środowisku głównym wymaga Y w wersji 1.0. Jeżeli uruchomimy Julię w środowisku głównym i zawołamy using Y załadowana zostanie wersja 1.0. Jeżeli teraz przejdziemy do środowiska X (activate X), to wersja 2.0 modułu Y nie zostanie załadowana, bo załadowania jest już wersja 1.0. Subtelne różnice mogą spowodować trudne do wyśledzenia błędy.

Kolejny problem wynika ze zmian jakie mogą przynieść aktualizacje. Jeżeli polegamy na wersji zainstalowanej w środowisku głównym, to po aktualizacji pakietów (] up) może się coś zmienić. Być może w środowisku X ta zmiana jest potrzebna, ale w środowisku Z coś zepsuje. Im więcej pakietów w środowisku głównym, tym większa szansa na konflikty wersji.

Dlatego generalnie powinniśmy unikać zaśmiecania głównego środowiska nadmierną liczbą pakietów i pracować głównie w środowiskach związanych z danym projektem. Umożliwia to powrót do odpowiednich wersji, nawet po dłuższym czasie, kiedy aktualizacje mogą zmienić zachowanie, czy nawet API bibliotek. Bezpieczne w środowisku głównym pakiety będą takie takie jak Revise, Infiltrator, czy BenchmarkTools, które pomagają w pisaniu kodu czy jego optymalizacji lub debuggowaniu, bo szansa, że są bezpośrednio wymagane w projekcie jest raczej nikła, a zapewne często będziemy ich potrzebować.

Aby uniknąć konieczności tworzenia środowiska i instalowania bibliotek za każdym razem, gdy chcemy przetestować kawałek kodu lub zrobić coś na szybko (np. narysować wykres), możemy zrobić dzielone środowisko (np. @scratch), w którym ewentualnie będziemy instalować cały bałagan, bez szkody dla głównego środowiska.

CC BY-SA 4.0 Krzysztof Miernik. Last modified: January 08, 2025. Website built with Franklin.jl and the Julia programming language.