GRUtils

W tej części zajmiemy się biblioteką GRUtils. Logika tej biblioteki to model maszyny stanowej (state machine), która jest może prostsza niż np. gramatyka grafiki mniej lub bardziej ściśle używana przez inne biblioteki.

using GRUtils

x = -2:0.1:2
plot(x, x.^2 .- 1)
hold(true)
plot(x, 2 .* x .+ 1)
ylim(-2, 4)
legend("\$f(x) = x^2 + 1\$", "\$g(x) = 2x + 1\$")
xlabel("\$x\$")
ylabel("\$y\$")

Funkcja plot tworzy wykres, dokładna składnia to:

plot(x[, y, spec; kwargs...])
plot(x1, y1, x2, y2...; kwargs...)
plot(x1, y1, spec1...; kwargs...)

W najprostszej wersji można zatem podać jedynie jeden wektor, wtedy są one interpretowane jako wartości Y, a wartości X są przypisywane od 1.

hold(false)
x = rand(10)
plot(x)

Kolejna wersja to podanie wartości x i y (jak w pierwszym przykładzie). Wreszczie możliwe jest podanie wielu wektorów, które stworzą wykresy parami x1, y1, x2, y2, ...

x = 0:0.1:2
plot(x, x, x, x.^2, x, x.^3)

Zmienna spec pozwala na podanie typu linii i znacznika według składni matplotlib:

• Postać [marker][line][color]

• znaczniki: , . o v ^ > < s p * h H + x D d 1..4 (i kilka innych)

• linie: - – .- :

• kolory: g r b c m y k w

hold(false)
plot(x, x, "Hg")

Dodatkowo specyfikacje linii i znaczników mogą być podane przez argumenty kluczowe

plot(x, x.^3 - x.^2, "-o", linewidth=1.5, markersize=0.5, linecolor=0xff0000, markercolor=0x00ff00)

W pierwszym przykładzie pojawiło się polecenie hold(true) i hold(false). Domyśle wykres jest w stanie hold(false), co oznacza, że kolejne wywołanie polecenia plot tworzy nowy wykres. hold(true) powoduje, że wykres jest dodawany do poprzedniego. Podobnie działa oplot (ze składnią jak plot) z tą różnicą w stosunku do hold, że zakres osi nie jest automatycznie zmieniany.

hold(false)
plot(x, x, "b*")
hold(true)
plot(x.^2, x, "rs")

hold(false)
plot(x, x, "g:")
oplot(x.^2, x, "k--")

Inne rodzaje wykresów to:

• scatter(x, y, s, c) - wykres punktów (x, y) z możliwością zmiany rozmiaru (s) i koloru (c)

• stem - wykres punktów ze słupkami

• errorbar - wykres z błędami w osi Y

• barplot - wykres słupkowy

• polar - wykres we współrzędnych walcowych (r, $\phi$)

Wykres powierzchni

x = -1:0.1:1
y = -1:0.1:1
z = x'.^2 .+ y.^2
println(size(z))
surface(x, y, z)

wireframe(x, y, z)
rotate(10)
tilt(0)

Wykres konturowy

x = -1:0.01:1
y = -1:0.01:1
f(x, y) = x^2 + y^2
contour(x, y, f)

Mapa

Mapa heatmap to inny sposób przedstawiania danych 3D, gdzie amplituda jest zaznaczona skalą kolorową. Wystarczy podanie 2D tablicy danych, lub opcjonalne wektory x i y definujące osie. Jeżeli dane (z) mają rozmiar $NxM$ to wektory powinny być rozmiaru $N-1$ i $M-1$.

hold(false)
x = -1:0.1:1
y = -1:0.1:1
z = x[1:end-1]'.^2 .+ y[1:end-1].^2
println(size(x), " ", size(y), " ",size(z))
heatmap(y, x, z)

Pole wektorowe

Pole wektorowe na płaszczyźnie można narysować funkcją quiver(x, y, u, v) gdzie x, y to początek wektora, a u, v jego długość.

x = repeat(-1:0.11:1, inner=20)
y = repeat(-1:0.11:1, outer=20)
u = 2 .* x
v = 2 .* y
quiver(x, y, u, v, arrowscale=0.1)
ylim(-1.2, 1.2)

Inne rodzaje wykresów

• imshow(plik) - rysuje obraz graficzny (z pliku lub z macierzy rgb)

• volume - trójwymiarowy wykres (x, y, z) intensywności v

Polecenia sterujące

Wykresy potrzebują dodatkowych informacji, ustawienia osi itp. Służą do tego

• title - tytuł wykresu

• xlabel/ylabel - tytuły osi

• grid(true) - siatka

• xlim/ylim - zakresy osi

• xlog(true)/ylog - skala logarytmiczna

• legend - legenda wykresów

• annotations(x, y, s) - napisy na wykresie

• xticks(minor, [major])/yticks - znaczniki minor określa co ile jest mały (np. 0.1), major określa co ile małych jest duży (z legendą) np. xticks(0.1, 10)

Wykorzystamy większość z tych możliwości w przykładzie nieco bardziej skomplikowanego wykresu. Tajemnicze mogą się wydawać jedynie współrzędne podane w poleceniu annotations. Otóż okazuje się, że to polecenie ignoruje fakt logarytmicznej skali i zachowuje się jakby była ona liniowa (niezależnie od kolejności poleceń)! Dochodzimy też do kresu możliwości GR jeżeli chodzi o dobór czcionek, wielkości i innych elementów.

f(x) = @. sin(4*x)^2 * exp(-x)
g(x) = @. sin(2*x)^2 * exp(-x/2)
x = 0:0.01:10

Figure((800, 600))
plot(x, f(x), "r")
hold(true)
plot(x, g(x), "b")
plot(x, exp.(-x), "--r", lw=2)
plot(x, exp.(-x./2), "--b", lw=2)
annotations([3.9, 5], [0.6, 0.75], ["\$e^{-x}\$", "\$e^{-x/2}\$"])

xlabel("\$x\$")
ylabel("\$f(x)\$")
grid(false)
ylim(1e-4, 1)
ylog(true)
xticks(1, 2)
xlim(0, 10)
legend()

Wiele wykresów

Wykresy w GRUtils są przechowywane w obiekcie Figure. Możemy jednocześnie mieć kilka takich obiektów, bieżący możemy zmienić sprawdzić lub poleceniem gcf() (domyślnie bieżący jest ostatnio stworzony, zgodnie z logiką maszyny stanowej).

Wersje poleceń "modyfikujące" (plot!, title!) jako pierwszy argument biorą obiekt Figure i zmieniają go, nawet jeżeli nie jest on bieżącym wykresem.

Nowy wykres tworzony poleceniem Figure() może mieć zadany rozmiar (krotka (x, y)) oraz jednostki ("cm", "pix").

using GRUtils
x = 0:0.1:2
fig1 = Figure((300, 300), "pix")
plot(x, x.^2)
hold(true)

fig2 = Figure()
plot(x, x.^2 .- x)

plot!(fig1, x, x)
gcf(fig1)
plot(x, x.^3)

display(fig1)
#display(fig2)

Jeden wykres Figure może mieć kilka podwykresów tworzonych poleceniem subplot(rows, cols, n) (analogicznym jak w matplotlib). Podobnie jak w przypadku wielu wykresów, podwykresy można zmieniać przez modyfikujące wersje funkcji (title!, legend! ...), ale nie można dodawać wykresów (plot! musi mieć jako argument Figure)

Figure()

lfig = subplot(1, 2, 1)
plot(x, x.^2, "-or")
oplot(x, x.^3, "--sk")

rfig = subplot(1, 2, 2)
plot(x, 2 .* x, "-r")
oplot(x, 3 .* x.^2, "--k")

title!(lfig, "A")
title("B")

display(gcf())

Zapisywanie wykresów do pliku

savefig(plik, [fig]) zapisuje bieżący (lub podany) wykres do pliku. Rozszerzenie definiuje typ pliku ( .png, .jpg, .pdf, .ps, .gif i inne).

Zadanie

Odtworzyć poniższy wykres przedstawiający w dwuwymiarowym rzucie fukcję falową stanu 1s i 2p (0 i $\pm$1) atomu wodoru w górnych panelach. Dolne prezentują przekrój przez gęstość prawdopodobieństwa (czyli $\left|\psi\right|^2$) wzdłuż osi x lub y dla funkcji falowych. Wzory na funkcje falowe można znaleźć tutaj. Skala jest w Angstromach ($10^{-11}$ m), wartość promieniu Bohra można wpisać jako stałą.

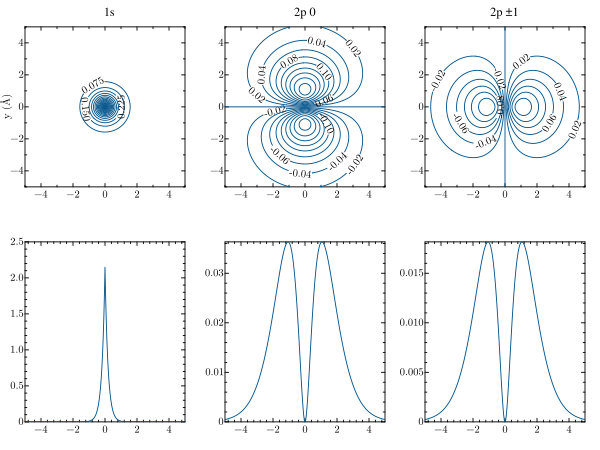
Wskazówka. Wielomian Hermite'a stopnia można n można dostać z modułu SpecialPolynomials (poniżej przykład).

using GRUtils
using SpecialPolynomials

Figure()

H2 = basis(Hermite, 2)
H3 = basis(Hermite, 3)

x = -2:0.01:2
plot(x, H2.(x), "-r")
hold(true)
plot(x, H3.(x), "-b")
ylim(-20, 20)
    
display(gcf())