Plots

Biblioteka Plots, chyba najbardziej popularna w Julii do tworzenia wykresów, w gruncie rzeczy nie jest biblioteką tworzącą wykresy, a jedynie metapakietem. Jego zadaniem jest stworzenie wspólnego interfejsu dla innych bibliotek. "Prawdziwe" biblioteki stojące za wykresami to

• GR

• PythonPlot (wrapper do matplotliba - Python)

• Gaston (wrapper do Gnuplota)

• PlotlyJS (wrapper do plotly - JavaScript)

• UnicodePlots (wykresy ASCII)

• PGFPlotsX (LaTeX - TikZ)

• InspectDR (głównie proste i szybkie interaktywne wykresy)

Backend można oczywiście zmieniać według możliwości i upodobań, domyślny to GR.

Najprostszy wykres

using Plots

x = 0:0.1:pi
y = cos.(x)
plot(x, y)

Jeżeli jako y podamy tabelę z kolumnami, to każda z nich zostanie interpretowana jako wykres

y = [cos.(x) sin.(x)]
println(typeof(y))
plot(x, y)

Istniejące wykresy można modyfikować poleceniami z wykrzyknikiem, np plot! doda wykres do poprzedniego

z = tan.(x)
plot!(x, z)

Cechy wykresu

Wszelkie cechy wykresu jakie chcemy modyfikować będą zawsze przekazywane jako nazwane atrybuty (np. title="Wykres 1"). Natomiast zmienne pozycyjne (takie jak x, y, ...) są traktowane zawsze jako dane.

plot(x, y, seriestype=[:stepmid :scatter], label=["cos" "sin"], lw=2)

unicodeplots()
plot(x, y, title="Wykres 1", label=["cos" "sin"], lw=2)

Listę atrybutów z danej kategorii można sprawdzić poleceniem plotattr (:Series, :Plot, :Axis, :Subplot). Dozwolone wartości danego atrybutu dostajemy podając jego nazwę.

plotattr(:Series)
plotattr("seriestype")
plotattr(:Plot)
plotattr(:Axis)

gr()
plot(x, tan.(x), framestyle=:origin, legend=:none, ylims=[-5, 5], xlabel="α", ylabel="tan(α)", linewidth=2)

Dużo typów wykresów (np. :scatter) oraz atrybutów (np. ylims) ma swoje wersje w postaci funkcji modyfikujących istniejacy wykres bądź sprawdzających stan (np. ylims() lub ylims(-10, 10)) co wprowadza alternatywną składnię zbliżoną do filozofii maszyny stanu.

println(ylims())
ylims!(-10, 10)
scatter!(x, cot.(x), marker=:rect, markersize=2)

Przykłady wykresów 2D

x = range(-1, 1, 100)
y = range(-2, 2, 100)
z = randn(length(x), length(y))
plot(x, y, z, seriestype=:heatmap, c=:blues)

function n2(x1, x2, μ1, μ2, σ1, σ2, r)
    N = 1 / (2 * pi * σ1 * σ2 * sqrt(1 - r^2))
    @. N * exp(-1 / (1 - r^2) * ((x1 - μ1)^2 / σ1^2 - 2 * r * (x1 - μ1) * (x2 - μ2) / (σ1 * σ2) + (x2 - μ2)^2 / σ2^2))
end

plot(x, y, n2(x', y, 0.0, 0.5, 0.2, 0.5, -0.5), seriestype=:contour, framestyle=:box, xlabel="x", ylabel="y")

Podwykresy

Kilka wykresów można objąć jednym poleceniem plot z atrybutem layout, wtedy będą tworzyły podwykresy większego wykresu. Atrybuty mogą teraz dotyczyć albo konkretnego podwykresu, albo wszystkich jednocześnie.

x = -2pi:0.05:2pi
println(x)
plot(plot(x, sin.(x)), 
     plot(x, cos.(x), color="black"), 
     plot(x, tan.(x), linestyle=:dashdot, linewidth=2), 
     plot(x, cot.(x), color="red", seriestype=:scatter, markershape=:cross, markersize=2), 
     layout=(2, 2), legend=:false, ylims=(-3, 3))

Taka składnia może wydawać się zagmatwana. Polecenie plot zwraca jednak tworzony wykres i można to wykorzystać do zapisania powyższego wykresu w nieco inny sposób.

p1 = plot(x, sin.(x))
p2 = plot(x, cos.(x), color="black")
p3 = plot(x, tan.(x), linestyle=:dashdot, linewidth=2)
p4 = plot(x, cot.(x), color="red", seriestype=:scatter, markershape=:cross, markersize=2) 
plot(p1, p2, p3, p4, layout=(2, 2), legend=:false, ylims=(-3, 3))

Tę metodę można wykorzystać np. w zbieraniu wielu wykresów. W poniższym przykładzie udajemy, że mamy 16 detektorów i patrzymy na położenie jakiejś linii.

using Distributions
using StatsBase

allplots = Any[]
for i in 1:16
    nd = Normal(50 + rand() * 20 - 10, 1 + rand() * 0.1)
    x = rand(nd, 10_000)
    h = fit(Histogram, x, 0:100)
    p = plot(h.edges[1][1:end-1], h.weights, seriestype=:stepmid, label="$i")
    push!(allplots, p)
end
plot(allplots..., layout=(4, 4))

Makro @layout pozwala tworzyć bardziej skomplikowane układy. Moduł Plots.PlotMeasures wprowadza jednostki względne (w/h - szerokość/wysokość) oraz bezwzględne (cm, px, itd.). LIterki a, b, c nie mają znaczenia i są tylko wewnętrznymi identyfikatorami kolejnych podwykresów w makrze @layout, a podkreślenie omija dane pole

using Plots.PlotMeasures
l = @layout[ a{0.25w} b{0.75h}
             _       c        ]
x = range(-2, 2, 100)
y = range(-2, 2, 100)
plot( plot(sum(n2(x', y, 0.0, 0.5, 1.0, 0.5, -0.5), dims=2), y, legend=:none, xlims=(0, 15), grid=false, minorgrid=false, ylims=(-2, 2), ylabel="Y"),
      plot(x, y, n2(x', y, 0.0, 0.5, 1.0, 0.5, -0.5), seriestype=:heatmap, framestyle=:box, colorbar=:none, xformatter=_->"", yformatter=_->""),
      plot(x, sum(n2(x', y, 0.0, 0.5, 1.0, 0.5, -0.5), dims=1)', legend=:none, ylims=(0, 15), grid=false, minorgrid=false, xlims=(-2, 2), xlabel="X"),
      layout=l
    )

Zapisywanie wykresów do pliku

savefig(plik) zapisuje bieżący wykres do pliku. Rozszerzenie definiuje typ pliku ( .png, .svg, .pdf).

Zadanie

Odtworzyć poniższy wykres przedstawiający w dwuwymiarowym rzucie fukcję falową stanu 1s i 2p (0 i $\pm$1) atomu wodoru w górnych panelach. Dolne prezentują przekrój przez gęstość prawdopodobieństwa (czyli $\left|\psi\right|^2$) wzdłuż osi x lub y dla funkcji falowych. Wzory na funkcje falowe można znaleźć tutaj. Skala jest w Angstromach ($10^{-11}$ m), wartość promieniu Bohra można wpisać jako stałą.

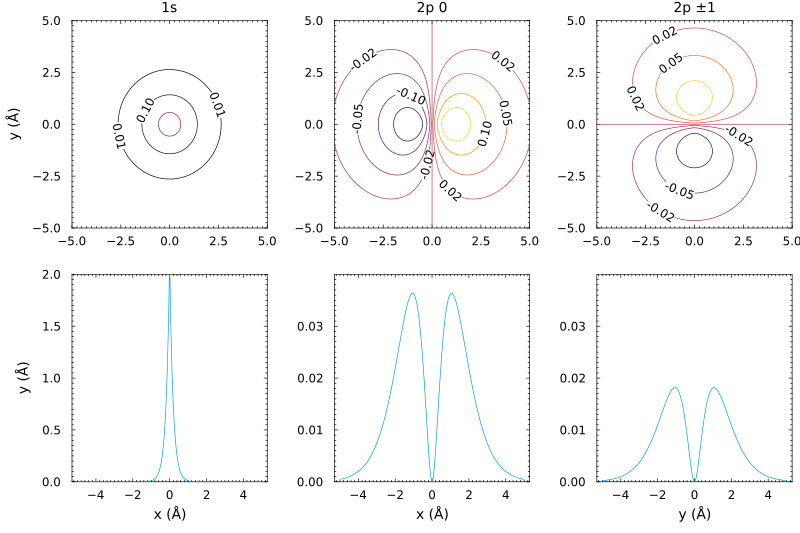
Wskazówka. Wielomian Hermite'a stopnia można n można dostać z modułu SpecialPolynomials (poniżej przykład).

using Plots
using SpecialPolynomials

H2 = basis(Hermite, 2)
H3 = basis(Hermite, 3)

x = -2:0.01:2
plot(x, H2.(x), seriestype=:lines, color=:red)
plot!(x, H3.(x), seriestype=:lines, color=:blue)