Makie
Makie jest bibioteką w pełni napisaną w Julii, co pozwala na pełną integrację i możliwości wykorzystania mechanizmów języka. W Makie mamy do dyspozycji kilka backendów, w zależności od planowanego sposobu użycia
CairoMakie - nieinteraktyne wykresy 2D o jakości potrzebnej do publikacji (grafika wektorowa)
GLMakie - interaktywne 2D i 3D wykresy, zoptymalizowane pod wydajność wyświetlania (czasem kosztem jakości) oparte o OpenGL
WGLMakie - oparte o WebGL, tworzy wykresy 2D i 3D do wyświetlania i interakcji w przeglądarkach
Zacznijmy od stworzenia prostego wykresu i omówimy jego składowe. Wyprodukujemy pseudo-pomiarowe dane z odrobiną losowego rozrzutu (udające rozpad promieniotwórczy) oraz będziemy udawać, że dopasowujemy do niego krzywą zaniku (w rzeczywistości znamy parametry rozkładu, więc nie musimy wołać żadnych funkcji dopasowujących, ale na wykresie ma to tak wyglądać).
Proste wykresy
using CairoMakie
fig = Figure()
ax = Axis(fig[1, 1])
x = 0:0.1:3
y = exp.(-x) .+ 0.05.*randn(size(x)[1])
scatter!(ax, x, y)
lines!(ax, x, exp.(-x))
current_figure()Pierwszym obiektem jaki tworzymy to Figure, czyli okienko (ramka) w którym będziemy umieszczać kolejne elementy. Dane będziemy wykreślać w obiekcie Axis (osie). Składnia fig[1, 1] mówi, że umieszczamy go w pierwszym rzędzie i pierwszej kolumnie naszego okna (jak można się od razu domyśleć, można zatem mieć ich więcej). Wreszcie polecenia scatter! oraz lines! rysują nasze dane za pomocą linii. Funkcja current_figure zwraca bieżący wykres (w przypadku REPL nie będzie potrzebne, ale notatnik Jupytera go potrzebuje).
W przypadku tak prostego wykresu zasadniczo wszystkie te elementy mogą być stworzone domyślnie za pomocą wersji lines bez wykrzynika, który domyślnie tworzy i ramkę i osie.
scatter(x, y)
lines!(x, exp.(-x))
current_figure()Tym niemniej rozbicie elementów wykresu na składowe pozwala zrozumieć w jaki sposób możemy go modyfikować, aby osiągnąć pożądany efekt oraz jak ewentualnie tworzyć znacznie bardziej skomplikowane wykresy.
Jeżeli chcemy uzyskać wykres o jakości potrzebnej do publikacji, to przede wszystkim wykres powinien mieć opisane osie, odpowiednio powiększoną czcionkę, ewentualnie usunięte pomocnicze linie, dobrane kolory, rozmiary punktów, posiadać legendę itd. Niektóre z tych wymogów należą do osi (np. rozmiar czcionki, linie pomocnicze), inne do serii danych (np. kolor).
Nasza oś ax posiada mnóstwo cech, które możemy zmieniać, po wpisania ax i naciśnięciu tabulatora powinny pojawić się podpowiedzi. Np. możemy wyłączyć linie pomocnicze w osi X. W ten sposób możemy krok po kroku pozmieniać pożądane elementy. Jeżeli z góry wiemy o jaki efekt nam chodzi, wszystko można zebrać w momencie tworzenia osi.
#ax. <TAB>, np.
ax.xgridvisible = falseZnaczenia większości parametrów użytych poniżej można domyśleć się po nazwie. Pewnego wyjaśnienia może wymagać limits, które w prezentowanej wersji przyjmuje argumenty (xmin, xmax, ymin, ymax), ale jeżeli któryś z parametrów jest nothing, to używana jest automatycznie dobierana wartość. limits ma kilka innych możliwości, które najlepiej sprawdzić w dokumentacji. O położeniu pomniejszych znaczników na osiach decyduje tu funkcja IntervalsBetween, która dzieli na zadaną liczbę równych odcinków.
fig = Figure()
ax = Axis(fig[1, 1];
xlabel="Time (s)",
xlabelsize=28,
xticklabelsize=24,
xminorticks=IntervalsBetween(5),
xminorticksvisible=true,
xgridvisible=false,
ylabel="Counts / 0.1 s",
ylabelsize=28,
yticklabelsize=24,
ygridvisible=false,
yminorticks=IntervalsBetween(5),
yminorticksvisible=true,
limits=(0, nothing, 0, nothing)
)
scatter!(ax, x, y, label="Exp.", marker=:rect, markersize=12)
lines!(ax, x, exp.(-x), label="Fit", color=:red, linestyle=:dash)
axislegend(ax; position=:rt, labelsize=24)
current_figure()Interaktywne wykresy
W tabelce podsumowującej umiejętności bibliotek pochwaliłem GLMakie za wysoką interaktywność. Aby nie być gołosłownym, przykład wykresu, w którym możemy kontrolować parametry funkcji opisującej tłumiony oscylator harmoniczny. Analogiczne rozwiązania znają Państwo z programów typu Mathematica. Tutaj wkładamy dwa suwaki, do obiektu SliderGrid. Zwykły suwak nie ma etykiety i wyświetlanej bieżącej wartości, a ta wygodna funkcja pozwala umieścić kilka pasków i je od razu opisać.
Bardziej tajemnicza wydaje się zapewne sposób wprowadzania zmian. Zajmuje się tym funkcja lift, która reaguje na zmianę zmiennych typu Observales (a takimi są położenia suwaków). Składnia do jest wygodniejszym sposobem zapisu anonimowej funkcji (x, y) -> ..., którą podawalibyśmy do lift. Czyli inny sposób zapisu wyglądałby tak:
y = lift((ω, γ)-> exp.(-γ .* t) .* cos.(sqrt(ω^2 + γ^2) .* t), sg.sliders[1].value, sg.sliders[2].value)co przy bardziej skomplikowanej funkcji byłoby jeszcze bardziej nieczytelne.
DataInspector() uruchamia interaktywny podgląd danych po najechaniu myszką na wybrany punkt.
Uwaga! Przykład nie będzie działał interaktywnie w notatniku Jupyter.
using GLMakie
GLMakie.activate!()
fig = Figure()
ax = Axis(fig[1, 1], limits=(0, 20, -1.1, 1.1), ylabel=L"y (t)", xlabel=L"t")
t = 0:0.1:20
sg = SliderGrid(
fig[2, 1],
(label="ω", range=0.1:0.1:3, format="{:.1f}", startvalue=2.0),
(label="γ", range=0.0:0.1:3, format="{:.1f}", startvalue=0.1)
)
y = lift(sg.sliders[1].value, sg.sliders[2].value) do ω, γ
Ω = sqrt(ω^2 + γ^2)
exp.(-γ .* t) .* cos.(Ω .* t)
end
lines!(ax, t, y)
DataInspector()
figZapisywanie wykresów do pliku
save(plik, fig) zapisuje bieżący wykres do pliku. Rozszerzenie definiuje typ pliku, GLMakie tworzy tylko .png, natomiast CairoMakie ma do wyboru .png, .svg i .pdf.
Skomplikowane układy
Spróbujemy zrobić teraz nieco bardziej skomplikowany wykres. Załóżmy, że mamy dane, które pochodzą z rozkładu binormalnego (dwuwymiarowego normalnego) z pewnymi wartościami średnimi i dyspersjami w X i Y oraz współczynnikiem korelacji. Chcemy narysować dwuwymiarową mapę wylosowanych wartości oraz odpowiedni rzuty na osie X i Y w osobnych wykresach.
Problem losowania i stworzenia histogramu rozwiążemy za pomocą bibliotek Distributions oraz StatsBase, gdzie znajdziemy odpowiednie funkcje.
using Distributions
using StatsBase
using LinearAlgebra
μx = -0.5
σx = 1.1
μy = 0.5
σy = 1.5
ρ = 0.8
mvn = MvNormal([μx, μy], [σx^2 ρ*σx*σy; ρ*σx*σy σy^2])
x = rand(mvn, 200_000)
h = fit(Histogram, (x[1, :], x[2, :]), (-5:0.1:5.1, -5:0.1:5.1))
h = normalize(h)Pierwsze podejście do problemu wygląda tak: w położeniu [1, 1] rysujemy mapę (countourf - mapa poziomic z wypełnionymi konturami), w położeniu [1, 2], narysujemy rzut na oś Y (pierwszy wymiar w macierzy), a [2, 1] - rzut na oś X (drugi wymiar macierzy).
using CairoMakie
CairoMakie.activate!()
fig = Figure(size = (800, 800))
axc = Axis(fig[1, 1]; xlabel="X", ylabel="Y")
axb = Axis(fig[2, 1]; xlabel="X", ylabel="Prob. density")
axr = Axis(fig[1, 2]; xlabel="Prob. density", ylabel="Y")
contourf!(axc, h.edges[1][1:end-1], h.edges[2][1:end-1], h.weights)
stairs!(axr, vec(sum(h.weights, dims=1)), collect(h.edges[1][1:end-1]))
stairs!(axb, collect(h.edges[2][1:end-1]), vec(sum(h.weights, dims=2)))
current_figure()Rysunek jest w miarę w porządku, ale wymaga teraz trochę dopieszczenia.
Mapa może być większa, a rzuty odpowiednio mniejsze w osiach zliczeń
Oś Y w rzucie Y, mogłaby być z prawej, zamiast lewej strony
Skale powinny zaczynać się w tym samym miejscu
Znaczniki mogłyby być lepiej rozmieszczone
Nie chcemy pomocniczych linii
Chcemy większe czcionki
Przydałby się informacja o skali kolorowej, najlepiej na górze, aby nie zaburzać położeń rzutów
fig = Figure(size = (800, 800))
gc = GridLayout()
fig[1, 1] = gc
axc = Axis(gc[2, 1])
axb = Axis(fig[2, 1]; xlabel=L"$X$", ylabel="Prob. density",
limits=(-5, 5, 0, 4),
xlabelsize=28,
xticklabelsize=24,
xminorticks=IntervalsBetween(5),
xminorticksvisible=true,
xgridvisible=false,
ylabelsize=28,
yticklabelsize=24,
yminorticks=IntervalsBetween(5),
yminorticksvisible=true,
ygridvisible=false,
)
gr = GridLayout()
fig[1, 2] = gr
axr = Axis(gr[1, 1]; xlabel="Prob. density", ylabel=L"$Y$",
limits=(0, 4, -5, 5),
xaxisposition=:top,
xlabelsize=28,
xticklabelsize=24,
xminorticks=IntervalsBetween(5),
xminorticksvisible=true,
xgridvisible=false,
yaxisposition=:right,
ylabelsize=28,
yticklabelsize=24,
ylabelrotation=0,
yminorticks=IntervalsBetween(5),
yminorticksvisible=true,
ygridvisible=false,
)
hidedecorations!(axc)
linkxaxes!(axc, axb)
linkyaxes!(axc, axr)
gr.alignmode = Mixed(top=-38)
colsize!(fig.layout, 1, Relative(2/3))
rowsize!(fig.layout, 1, Relative(2/3))
cf = contourf!(axc, h.edges[1][1:end-1], h.edges[2][1:end-1], h.weights)
text!(axc, [-4.8], [3.8], text="a)", color=:white, fontsize=28)
cb = Colorbar(gc[1, 1], cf, ticklabelsize=24, vertical=false)
stairs!(axr, vec(sum(h.weights, dims=1)), collect(h.edges[1][1:end-1]))
text!(axr, [3.5], [3.8], text="b)", fontsize=28, align=(:right, :bottom))
stairs!(axb, collect(h.edges[2][1:end-1]), vec(sum(h.weights, dims=2)))
text!(axb, [-4.8], [3], text="c)", fontsize=28)
resize_to_layout!(fig)
current_figure()Uff! Ale co tu się dokładnie stało? Popatrzmy na listę żądań i sprawdzimy krok po kroku jak zostały spełnione.
Mapa może być większa, a rzuty odpowiednio mniejsze w osiach zliczeń
Kolejne wykresy wkładane są w oczka siatki (fig[1, 1], fig[1, 2], itd.). W poprzedniej wersji każdy wykres miał do dyspozycji tyle samo miejsca. Tu zmieniamy propocje kolumn i wierszy, aby kolorowa mapa była największa. Tak naprawdę dzieje się to za pomocą:
colsize!(fig.layout, 1, Relative(2/3))
rowsize!(fig.layout, 1, Relative(2/3))Przydałby się informacja o skali kolorowej, najlepiej na górze, aby nie zaburzać położeń rzutów
To żądanie trochę nabroiło. Otóż siatki w których umieszczane są elementy wykresu mogą być zagnieżdżone. Wykorzystaliśmy to do umieszczenia zamiast mapy w polu [1, 1], nowej siatki gc = GridLayout(), która została podzielona na gc[1, 1] zawierające pasek kolorowy i gc[2, 1] zawierający mapę.
To niestety ma swoje konsekwencje jeżeli chodzi o ustawienie względem innych wykresów. Wykres z prawej strony byłby teraz wyrównany względem paska i jego górna krawędź nie pasowałaby do mapy. Dlatego jego polu fig[1, 2] zostało również nadana siatka gr. Co ciekawe zawiera tylko jedno pole gr[1, 1], ale dzięki temu możemy niezależnie zmienić jego parametry dotyczące wyrównania. I tak
gr.alignmode = Mixed(top=-38)Oznacza, że tryb wyrównywania jest mieszany (domyślny tryb to Auto lub Fixed, Mixed ma niektóre krawędzie Auto, inne Fixed). Wartość jest dobrana tak, aby górna krawędź wykresu (liczy się razem z etykietą!) pasowała do mapy.
Skale powinny zaczynać się w tym samym miejscu
Tu oprócz użycia limits = ... mamy też
hidedecorations!(axc)
linkxaxes!(axc, axb)
linkyaxes!(axc, axr)Pierwsze polecenie usuwa wszelkie dekoracje (znaczniki, etykiety) z wykresu mapy (są też odpowiednio hidexdecorations!, hideydecorations!), które nie będą potrzebne, bo osie opiszemy na rzutach. Następnie osie X mapy i dolnego wykresu są ze sobą powiązane i podobnie osie Y mapy i prawego wykresu. Ewentualna zmiana skali powiązanych osi zmienia je automatycznie w pozostałych.
Oś Y w rzucie Y, mogłaby być z prawej, zamiast lewej strony
Ten problem (i przy okazji przeniesienie osi X na górę) załatwia nam
xaxisposition=:top,
yaxisposition=:right,Znaczniki mogłyby być lepiej rozmieszczone
Po zmianie granic na -5,5 naturalne było wprowadzenie 5 mniejszych znaczników (x/yminorticks=IntervalsBetween(5)).
Nie chcemy pomocniczych linii
Tak jak wcześniej x/ygridvisible=false
Chcemy większe czcionki
To już również było ylabelsize=28, yticklabelsize=24, itd. Przy okazji pojawiły się oznaczenia podwykresów a, b, c. Do tego oczywiście służą polecenia
text!(axc, [-4.8], [3.8], text="a)", color=:white, fontsize=28)Zadanie
Odtworzyć poniższy wykres przedstawiający w dwuwymiarowym rzucie fukcję falową stanu 1s i 2p (0 i 1) atomu wodoru w górnych panelach. Dolne prezentują przekrój przez gęstość prawdopodobieństwa (czyli ) wzdłuż osi x lub y dla funkcji falowych. Wzory na funkcje falowe można znaleźć tutaj. Skala jest w Angstromach ( m), wartość promieniu Bohra można wpisać jako stałą.
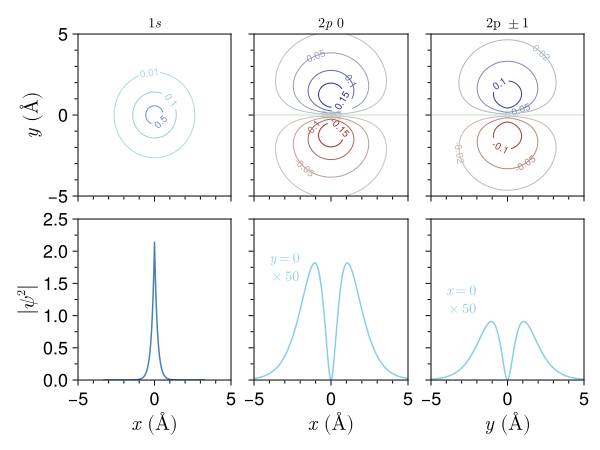
Wskazówka. Wielomian Hermite'a stopnia można n można dostać z modułu SpecialPolynomials (poniżej przykład).
using SpecialPolynomials
H2 = basis(Hermite, 2)
H3 = basis(Hermite, 3)
x = -2:0.01:2
lines(x, H2.(x), label="n=2")
lines!(x, H3.(x), label="n=3")
axislegend()
current_figure()