Error avoiding quantum codes and dynamical stabilization of Grover's algorithm

Deutsche Physikalische Gesellschaft | Institute of Physics

Athens login

This volume

| Abstract

| Content finder

New J. Phys. 2 (2000) 19
PII: S1367-2630(00)13022-8

Error avoiding quantum codes and dynamical stabilization of Grover's algorithm

Michael Mussinger, Aldo Delgado and Gernot Alber

Abteilung für Quantenphysik, Universität Ulm, D-89069 Ulm, Germany

New Journal of Physics 2 (2000) 19.1-19.16
Received 31 March 2000; online 12 September 2000

Abstract. Dynamical stabilization properties of error avoiding quantum codes are investigated beyond the perturbative regime. As an example Grover's search algorithm and its behaviour under a particular class of coherent errors are studied. Numerical examples which demonstrate that error avoiding quantum codes may be capable of stabilizing quantum algorithms well beyond the regime for which they were designed originally are presented.

Contents

1. Introduction

According to a suggestion of Feynman [1] quantum systems not only are of interest for their own sake but also might serve for practical purposes. Thus they may be used for simulating other quantum systems which are less convenient to handle or they may be used for solving computational problems more efficiently than can be achieved by any other classical means. Two well known examples demonstrating the latter point are Shor's factorization algorithm [2] and Grover's search algorithm [3,4].

Quantum systems which are capable of performing quantum algorithms are called quantum computers. So far several physical systems have been considered as potential candidates for quantum computers, such as trapped ions [5], nuclear spins of molecules [6] and, in the context of cavity quantum electrodynamics, atoms interacting with a single mode of the radiation field [7]. To describe the operation of a quantum computer theoretically it is advantageous to refrain from a detailed physical description of the particular quantum system involved. Thus, in analogy to the spirit of computer science, it is more useful to concentrate on those particular aspects which are essential for the performance of quantum computation. On this abstract level a generic quantum computer consists of m distinguishable smaller quantum systems which are frequently chosen as two-level systems with basis states $\vert 1\rangle$ and $\vert\rangle$ , for example. The quantum information which can be stored in one of these two-level systems is called a qubit. Thus the state space of a generic quantum computer is spanned by the so-called computational basis which consists of the corresponding 2^m product states $\vert b_0\rangle = \vert \ldots 00\rangle$ , $\vert b_1\rangle = \vert \ldots 01\rangle$ , ... $\vert b_{2^m}\rangle = \vert 1 \ldots 11\rangle$ .

A typical quantum computation proceeds in several steps. Firstly, the quantum computer is prepared in an initial state. Secondly, a certain sequence of unitary transformations is performed. They are called quantum gates and usually entangle the m qubits. Thirdly, the final result is measured. Typically the solution of a particular computational problem is obtained with a certain probability only. A general quantum algorithm takes advantage of an essential feature of quantum theory, namely the interference between probability amplitudes and the fact that the dimensionality D of the state space of m distinguishable qubits increases exponentially with the number of qubits, i.e. D = 2^m. Among the best known quantum algorithms are the Shor algorithm [2] and Grover's search algorithm [3,4,8]. In the latter algorithm a particular sequence of quantum gates (see figure 1) allows one to find a specific item in an unsorted database much faster than can be done with any other known classical means. This quantum algorithm has already been realized experimentally for a small number of qubits [9].

$\begin{figure} \hspace{6pc} \epsfxsize=18pc \epsfbox {1302201.eps} \end{figure}$

Figure 1. A quantum mechanical version of the classical XOR gate as an example of a quantum gate (a CNOT gate). The input state $\vert x,y\rangle$ is mapped onto the output state $\vert x,x\oplus y\rangle$ .

Among the main practical problems one has to overcome in the implementation of quantum algorithms are non-ideal performances of the quantum gates [10] involved and random environmental influences, both of which tend to affect the relevant quantum coherence. To protect quantum computation against such errors, two major strategies have been proposed recently, namely active quantum error correction [11]-[19] and passive error avoiding quantum codes [20]-[24]. Active quantum error correction may be viewed as a generalization of classical error correction techniques to the quantum domain. Typically, active quantum error correction involves a properly chosen sequence of frequently repeated measurements. The approach of the error avoiding quantum codes is different. The main idea is to encode the logical information in one of those subspaces of the relevant Hilbert space which is not affected by the physical interactions responsible for the occurrence of errors [20]-[24]. Both theoretical approaches to error correction rely on the concept of redundancy, which is also fundamental for classical error correcting codes [25]. It is expected that error avoiding codes will offer more effective means for stabilizing quantum algorithms. This expectation is based on two facts. Firstly, there is no need for control measurements which are an essential ingredient of any active error correcting code. Secondly, in many cases a smaller number of physical qubits is needed for the representation of a given number of logical qubits.

In the subsequent discussion it is demonstrated that this is indeed the case. By considering Grover's quantum search algorithm it is shown that non-ideal perturbations may be corrected dynamically in an efficient way with the help of an appropriate error avoiding quantum code. By generalizing recent perturbative results [26], it is demonstrated that error avoiding quantum codes may be applicable well beyond the type of errors for which they were originally designed. As a particular example, we discuss coherent errors which may arise from systematic detunings of the physical qubits of the quantum computer from the frequency of the light pulses which realize the required quantum gates. The corresponding error avoiding quantum code with the lowest degree of redundancy is more efficient at encoding quantum information than is any possible active error correcting code which saturates the quantum Hamming bound. The error avoiding quantum code [20] used consists solely of states which are factorizable in the computational basis. In this respect it differs significantly from the recently proposed error avoiding code of [21], for example, which also involves entangled states. Such factorizable codes may offer practical advantages insofar as the implementation of quantum gates in error avoiding subspaces is concerned.

The paper is organized as follows. In section 2 basic facts about Grover's quantum search algorithm are summarized. It is demonstrated that, for large databases, the dynamics of this quantum algorithm can be described by a two-level Hamiltonian which implies that there are Rabi oscillations between the initial state and the sought state. In section 3 general ideas underlying the construction of error avoiding quantum codes are discussed. An efficient error avoiding quantum code which is capable of stabilizing Grover's algorithm against a particular class of coherent errors is presented. The redundancy of this code is discussed and compared with that resulting from active error correcting codes which saturate the quantum Hamming bound. Numerical examples demonstrating the stabilizing capabilities of this error avoiding quantum code are presented in section 4.

2. Grover's quantum search algorithm

Consider an unsorted database with N items and a certain item x₀ for which you are searching. As a particular example you can imagine a telephone directory with N entries and a particular telephone number x₀ for which you are looking. Furthermore, assume that you are given a black box, i.e. a so-called oracle, which can decide whether an item is x₀. Thus, in mathematical terms you are given a Boolean function

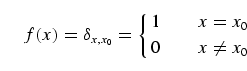$\begin{equation} f(x) = \delta_{x,x_0} =\cases{1 & $x = x_0$\cr 0 & $x \neq x_0$} \end{equation}$

(1)

with $\delta_{a,b}$ denoting the Kronecker delta function. Usually the elements x of the database are assumed to be described by the N integers between zero and N-1. Assuming that each application of the oracle requires one elementary step, a classical random search process will require N-1 steps in the worst case and one step in the best possible case. Thus, on average a classical algorithm will need N/2 steps to find the sought item x₀. It has been shown by Grover [3,4] that, with the help of his quantum search algorithm, this task can be performed in $O(\surd N)$ steps with a probability arbitrarily close to unity. The basic idea of this quantum algorithm is to rotate the initial state of the quantum computation in the direction of the sought state $\vert x_0\rangle$ by a sequence of unitary quantum versions of the oracle. It will become apparent from the subsequent discussion that, apart from Hadamard transformations, the dynamics of this rotation is analogous to a Rabi oscillation between the initially prepared state and the sought state $\vert x_0\rangle$ . It has been shown by Zalka [27] that Grover's quantum search algorithm is optimal.

$\begin{figure} \hspace{6pc} \epsfxsize=12pc \epsfbox {1302202.eps} \end{figure}$

Figure 2. A schematic representation of the quantum oracle ${\cal U}_f$ . For $f(x)\equiv x$ this quantum gate reduces to the CNOT gate of figure 1; for $\vert a\rangle \equiv \vert a_0\rangle = 1/\surd 2 (\vert\rangle - \vert 1\rangle )$ it results in the conditional phase inversion I_x₀ of equation (9) that is needed in Grover's algorithm.

2.1. The characteristic gate sequence of Grover's search algorithm

In Grover's quantum search algorithm every element of the database is represented by a state of the computational basis of the quantum computer. Thus a database which is represented by m qubits has N = 2^m distinguishable elements. The state $\vert\ldots0110\ldots0\rangle$ of the computational basis, for example, corresponds to the element 0...0110...0 of the database in binary notation. The quantum oracle ${\cal U}_f$ (see figure 2) is determined completely by the Boolean function of equation (1) and is represented by a quantum gate, i.e. by the unitary and Hermitian transformation

$\begin{equation} {\cal U}_f: \vert x,a\rangle \to \vert x, f(x) \oplus a\rangle. \end{equation}$

(2)

Thereby $\vert x\rangle$ is an arbitrary element of the computational basis and $\vert a\rangle$ is the state of an additional ancillary qubit which is discarded later. The symbol $\oplus$ denotes addition modulo 2. This unitary form of the oracle depends on the Boolean function f(x). Insofar as complexity estimates are concerned, it is assumed that this unitary transformation requires one elementary step. This assumption is analogous to the complexity estimate of the corresponding classical version of this search problem.

For the subsequent discussion it is important to note that the elementary rotations in the direction of the sought quantum state $\vert x_0\rangle$ which are the key ingredient in Grover's algorithm can be performed with the help of this unitary oracle. Thus such a rotation can be performed without explicit knowledge of the state $\vert x_0\rangle$ . Implicit knowledge of it through the values of the Boolean function f(x) is sufficient. For large values of N it turns out that the number of elementary rotations needed to prepare the state $\vert x_0\rangle$ is $O(\surd N)$ . To implement such an elementary rotation from the initial state $\vert s\rangle = \vert\ldots0\rangle$ , for example, towards the final state $\vert x_0\rangle$ two different types of quantum gates are needed, namely Hadamard gates and controlled phase inversions.

A Hadamard gate is a unitary one-qubit operation. It produces an equally weighted superposition of the two basis states according to the rule

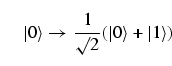$\begin{equation} \vert\rangle \to \frac{1}{\surd 2} ( \vert\rangle + \vert 1 \rangle) \end{equation}$	(3)
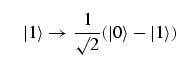$\begin{equation} \vert 1\rangle \to \frac{1}{\surd 2} ( \vert\rangle - \vert 1 \rangle ) \end{equation}$	(4)

or, in matrix notation,

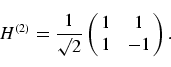$\begin{displaymath} H^{(2)} = \frac{1}{\surd 2} \left(\matrix{1 & 1\cr 1 & -1}\right). \end{displaymath}$

An m-qubit Hadamard gate H^{(2^m)} is defined by the m-fold tensor product, i.e. $H^{(2^m)}=H^{(2)}\otimes \cdots\otimes H^{(2)}$ . Thus, for two qubits, for example, H^(2²) is represented by the matrix

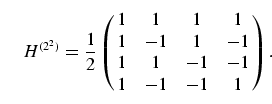$\begin{equation} H^{(2^2)} = \frac{1}{2} \left(\matrix{1 & 1 & 1 & 1\cr 1 & -1 & 1 & -1\cr 1 & 1 & -1 & -1\cr 1 & -1 & -1 & 1}\right). \end{equation}$

(5)

The Hadamard transformation is Hermitian and unitary. An arbitrary matrix element H^{(2^m)}_i,j of a Hadamard transformation may be written in the general form

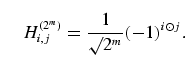$\begin{equation} H^{(2^m)}_{i,j} = \frac{1}{\surd 2^m} (-1)^{i \odot j}. \end{equation}$

(6)

Here i and j denote binary numbers and the multiplication $\odot$ is bitwise modulo 2, i.e. for i = 1, j = 3 and m = 2, one obtains $H^{(4)}_{1,3} = \frac12 (-1)^{( 01 \odot 11 )} = \frac12( -1) ^ {( 0\times 1 + 1 \times 1 )} = - \frac12$ . It has been shown by Grover [3,4] that this Hadamard transformation can be replaced by any other unitary one-qubit operation.

The remaining quantum gates needed for the implementation of the necessary rotation are controlled phase inversions with respect to the initial and sought states $\vert s\rangle = \vert\ldots0\rangle$ and $\vert x_0\rangle$ . A controlled phase inversion with respect to a state $\vert x\rangle$ changes the phase of this particular state by an amount $\pi$ and leaves all other states unchanged. Thus the phase inversion I_s with respect to the initial state $\vert s\rangle$ is defined by

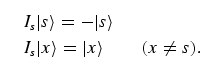$\begin{equation} \eqalign{ I_s \vert s\rangle = - \vert s\rangle\cr I_s \vert x\rangle = \vert x\rangle\tqs (x \neq s ).} \end{equation}$

(7)

For two qubits, for example, its matrix representation is given by

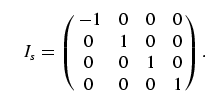$\begin{equation} I_s = \left(\matrix{- 1 & 0 & 0 & 0\cr 0 & 1 & 0 & 0\cr 0 & 0 & 1 & 0\cr 0 & 0 & 0 & 1}\right). \end{equation}$

(8)

The controlled phase inversion I_x₀ with respect to the sought state $\vert x_0\rangle$ is defined in an analogous way. Because the state $\vert x_0\rangle$ is not known explicitly but only implicitly through the property f(x₀) = 1, this transformation has to be performed with the help of the quantum oracle. This task can be achieved by preparing the ancillary of the oracle of equation (2) in the state $\vert a_0\rangle = (1/\surd 2) ( \vert\rangle - \vert 1\rangle )$ . As a consequence one obtains the required properties for the phase inversion I_x₀, namely

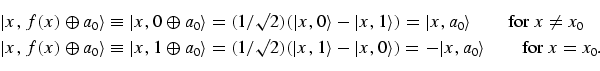$\begin{equation} \eqalign{ \fl\vert x,f(x) \oplus a_0 \rangle \equiv \vert x, 0 ... ...\vert x,0\rangle) = - \vert x,a_0\rangle\tqs \mbox{for } x =x_0. } \end{equation}$

(9)

One should bear in mind that this controlled phase inversion can be performed with the help of the quantum oracle of equation (2) only without explicit knowledge of the state $\vert x_0\rangle$ .

Grover's algorithm starts by preparing all m qubits of the quantum computer in the state $\vert s\rangle = \vert\ldots0\rangle$ . An elementary rotation in the direction of the sought state $\vert x_0\rangle$ with the property f(x₀) = 1 is achieved by the gate sequence

Q = - I_s H^{(2^m)} I_x₀ H^{(2^m)}.

(10)

In order to rotate the initial state $~\vert s\rangle$ into the state $\vert x_0\rangle$ one has to perform a sequence of n such rotations and a final Hadamard transformation at the end, i.e.

$\begin{equation} \vert f\rangle = H Q^n \vert s\rangle. \end{equation}$

(11)

The effect of the elementary rotation Q is demonstrated in figure 3 for the case of three qubits, i.e. m = 3. The first Hadamard transformation H^(2³) prepares an equally weighted state. The subsequent quantum gate I_x₀ inverts the amplitude of the sought state $\vert x_0\rangle = \vert 111\rangle$ . Together with the subsequent Hadamard transformation and the phase inversion I_s, this gate sequence Q amplifies the probability amplitude of the sought state $\vert 111\rangle$ . In this particular case an additional Hadamard transformation finally prepares the quantum computer in the sought state $\vert 111\rangle$ with a probability of 0.88.

$\begin{figure} \leavevmode\epsfxsize=15pc\leavevmode \epsfbox {1302203a.eps} \leavevmode\epsfxsize=15pc\leavevmode \epsfbox {1302203b.eps} \end{figure}$ $\begin{figure} \leavevmode\epsfxsize=15pc\leavevmode \epsfbox {1302203c.eps} \leavevmode\epsfxsize=15pc\leavevmode \epsfbox {1302203d.eps} \end{figure}$ $\begin{figure} \leavevmode\epsfxsize=15pc\leavevmode \epsfbox {1302203e.eps} \leavevmode\epsfxsize=15pc\leavevmode \epsfbox {1302203f.eps} \end{figure}$

Figure 3. Amplitude distributions resulting from the various quantum gates involved in Grover's quantum search algorithm for the case of three qubits. The quantum states which are prepared by these gates are (a) $\vert s\rangle = \vert00\rangle$ , (b) $H^{(2^m)}\vert s\rangle$ , (c) $I_{x_0}H^{(2^m)}\vert s\rangle$ ,(d) $H^{(2^m)}I_{x_0}H^{(2^m)}\vert s\rangle$ , (e) $-I_s H^{(2^m)}I_{x_0}H^{(2^m)}\vert s\rangle$ and (f) $-H^{(2^m)}I_s H^{(2^m)}I_{x_0}H^{(2^m)}\vert s\rangle$ . The sought state $\vert x_0\rangle$ entering the Boolean function of equation (1) is assumed to be the state $\vert 111\rangle$ .

In order to determine the dependence of the ideal number of repetitions n on the number of qubits m, it is convenient to analyse the repeated application of the gate sequence Q according to equation (11) in terms of the two states $\vert s\rangle$ and $\vert v\rangle =H^{(2^m)}\vert x_0\rangle$ whose overlap is given by $\epsilon = \langle s \vert v\rangle = \langle s \vert H^{(2^m)} \vert x_0 \rangle = 2^{-m/2}$ for m qubits. It is straightforward to show that the unitary gate sequence Q preserves the subspace spanned by these two states [3,4], i.e.

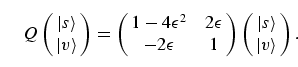$\begin{equation} Q\left(\matrix{\vert s\rangle\cr \vert v\rangle}\right) =\left(... ... 1}\right) \left(\matrix{\vert s\rangle\cr \vert v\rangle}\right). \end{equation}$

(12)

Thus Q acts like a rotation in the plane spanned by states $\vert s\rangle$ and $\vert v\rangle$ (see figure 4). The angle of rotation is given by $\varphi = {\rm arcsin}[2\epsilon(1-\epsilon^2)^{1/2}]$ .

$\begin{figure} \hspace{6pc} \epsfxsize=16pc \epsfbox {1302204.eps} \end{figure}$

Figure 4. Q is a rotation in the subspace spanned by states $\vert s\rangle$ and $\vert v\rangle$ .

After j iterations the amplitude of state $\vert v\rangle$ is given by [8]

$\begin{equation} \sin[ (2j +1) \epsilon ]. \end{equation}$

(13)

Therefore, the optimal number n of repetitions of the gate sequence Q is approximately given by

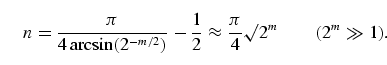$\begin{equation} n = \frac{\pi}{4\arcsin( 2^{-m/2} ) } -\frac{1}{2} \approx\frac{\pi}{4} \surd 2^m\tqs (2^m\gg 1). \end{equation}$

(14)

Finally, it should be mentioned that several generalizations of Grover's original search algorithm which consider arbitrary initial states have also been presented [28,29].

2.2. Hamiltonian representation of Grover's algorithm

If the database contains many elements, i.e. $N \equiv \epsilon^{-2}\gg 1$ ,the repeated application of the elementary rotation which is essential for Grover's search algorithm can be described by Hamiltonian quantum dynamics (an alternative Hamiltonian description has been introduced by Fahri and Gutmann [30]). The elementary rotation Q can be approximated by the relation

$\begin{equation} Q = \mbox{\bf 1} - \tau (\mathrm{i}/\hbar) {\bi H}_G (\epsilon) + O(\epsilon^2) \end{equation}$

(15)

which involves the Hamiltonian

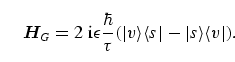$\begin{equation} {\bi H}_G = 2~\mathrm{i} \epsilon \frac{\hbar}{\tau} (\vert v \rangle \langle s \vert- \vert s \rangle \langle v \vert). \end{equation}$

(16)

The elementary time $\tau$ might be interpreted as the physical time required for performing the elementary rotation Q. The Hamiltonian of equation (16) describes the dynamics of a quantum mechanical two-level system whose degenerate energy levels $\vert s\rangle$ and $\vert v\rangle$ are coupled by a time-independent perturbation. To lowest order of $\epsilon$ these degenerate energy levels are orthogonal. The resulting oscillations between these coupled energy levels are characterized by the Rabi frequency $\Omega = 2 \langle s \vert v \rangle / \tau$ . Correspondingly, the repeated application of the elementary rotation Q can be determined with the help of Trotter's product formula [31], namely

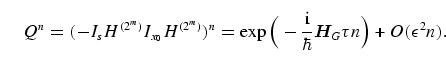$\begin{equation} Q^n = (- I_s H^{(2^m)} I_{x_0} H^{(2^m)})^n = \exp\bigg( - \frac{\mathrm{i}}{\hbar}{\bi H}_G \tau n \bigg) + O(\epsilon^2 n). \end{equation}$

(17)

Thus, in the framework of this Hamiltonian description, applying the elementary rotation Q n times is equivalent to a temporal evolution of the effective two-level quantum system over a time interval of magnitude $n\tau$ . This Hamiltonian description demonstrates that the physics behind Grover's quantum search algorithm is the same as the physics governing the Rabi oscillations between degenerate or resonantly coupled energy eigenstates. Since the errors entering equation (17) are of order $O(\epsilon^2 n)$ , this Hamiltonian description is applicable only as long as $\epsilon^2 n \equiv n/2^{m}\ll 1$ . Thus, for a given size of the database, it is valid only as long as the number of iterations is sufficiently small, i.e. $n \ll 2^m$ . However, because Grover's search algorithm needs approximately $(\pi\surd 2^{m}/4)$ steps to find the sought item, the main condition which restricts the validity of this Hamiltonian description is a large size of the database, i.e. $\epsilon^2 \equiv 1/N \ll 1$ .

$\begin{figure} \hspace{6pc} \epsfxsize=18pc \epsfbox {1302205.eps} \end{figure}$

Figure 5. The probability of being in the state $\vert x_0\rangle$ after $n = t/\tau$ iterations of Grover's quantum search algorithm for three qubits: the ideal dynamics according to the Hamiltonian time evolution characterized by equations (16) and (17) (broken line); and the non-ideal case of coherent errors characterized by equations (16)-(18) (full line) with detunings $\omega_1 = 0.5 \langle s \vert v \rangle / \tau$ , $\omega_2 = 0.3 \langle s \vert v \rangle / \tau$ and $\omega_3 = 0.2 \langle s \vert v \rangle / \tau$ .

2.3. An example of coherent errors

So far we have been concentrating on the ideal dynamics of Grover's quantum search algorithm. However, in practical applications it is very difficult to realize this search algorithm in an ideal way. Usually the ideal dynamics is affected by numerous perturbations. Physically one may distinguish two different kinds of errors, namely incoherent and coherent ones. Typically incoherent perturbations originate from a coupling of the physical qubits of a quantum computer to an uncontrollable environment. As a consequence the resulting errors are of a stochastic nature. Coherent errors may arise from non-ideal quantum gates which lead to a unitary but non-ideal temporal evolution of the quantum algorithm. A simple example of this type of errors is systematic detuning from resonance of the light pulses with which the required quantum gates are realized on the physical qubits. In the Hamiltonian formulation of Grover's algorithm such systematic detunings may be described by a perturbing Hamiltonian of the form

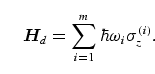$\begin{equation} {\bi H}_d = \sum_{i=1}^m \hbar \omega_i \sigma_z^{(i)}. \end{equation}$

(18)

In equation (18) it has been assumed that Grover's quantum algorithm is realized by m qubits and that the ith qubit is detuned with respect to the ideal transition frequency by an amount $\omega_i$ . A possible result is shown in figure 5. The Pauli spin-operator of the ith qubit is denoted $\sigma_z^{(i)}$ . In the presence of these systematic detunings and for a large number of qubits the dynamics of Grover's algorithm is described by the Hamiltonians of equations (16) and (18).

In order to obtain insight into the influence of this type of coherent errors, the performance of Grover's algorithm under repeated applications of the elementary rotation Q is depicted in figure 5. The dynamics of the ideal Grover algorithm for the case of three qubits, i.e. m = 3, is depicted by the broken line. The Rabi oscillations with frequency $\Omega = 2\langle v\vert s\rangle /\tau$ are clearly visible. The full line shows the probability of observing the quantum computer in the state $\vert x_0\rangle$ in a case in which all the qubits are detuned from their ideal resonance frequency. One notices the deviations from the ideal behaviour. Owing to the coherent nature of the errors, the temporal evolution of the non-ideal algorithm exhibits revival phenomena [32].

3. Error avoiding quantum codes

In general there are two different strategies for correcting errors in quantum information processing. Active quantum error correcting schemes may be viewed as generalizations of classical error correction techniques to the quantum domain [11]-[14]. Typically they involve a suitably chosen quantum code and a sequence of quantum measurements. A non-degenerate code, which is the simplest example, has to map all possible states which may result from arbitrary environmental influences onto orthogonal states. According to basic postulates of quantum theory these orthogonal quantum states can be distinguished and, from the result of a control measurement, one may restore the original quantum state. So far these general techniques have been applied mainly to the stabilization of static quantum memories [33].

The second possible error correction strategy, which seems to be suitable also for stabilizing quantum algorithms, is based on error avoiding quantum codes [20]-[24]. These latter methods rely on knowledge of basic properties of the relevant error. The main idea is to encode the quantum information in those subspaces of the Hilbert space which are not affected by the errors. This aim is achieved by restricting oneself to degenerate eigenspaces of the relevant error operators. Thus, in the special case of a single error operator, say E, the basis states $\{ \vert \psi_i \rangle \}$ of such an error-free subspace have to satisfy the relation

$\begin{equation} {\bi E} \vert \psi_i \rangle = c \vert \psi_i \rangle. \end{equation}$

(19)

Error avoiding quantum codes are completely degenerate error correcting codes in the sense that the code space is preserved under the influence of the errors and therefore no recovery operation is needed [34]. In the above-mentioned example of coherent errors which may affect Grover's algorithm this error operator is given by the Hamiltonian of equation (18), i.e. E = H_d. It is crucial for the success of an error avoiding code that the eigenvalue c of equation (19) does not depend on the states belonging to the error-free subspace. This implies that all possible elements of the error-free subspace of the general form $\sum_i \alpha_i \vert\psi_i\rangle$ are affected by the error operator in the same way, i.e.

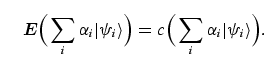$\begin{equation} {\bi E} \bigg(\sum_i \alpha_i \vert \psi_i \rangle\bigg) = c \bigg(\sum_i \alpha_i \vert \psi_i \rangle\bigg). \end{equation}$

(20)

It is apparent that a non-trivial error avoiding code is possible only if the eigenspace of the error operator E is degenerate.

3.1. An error avoiding quantum code stabilizing coherent errors

As an example of an error avoiding quantum code let us consider the case of coherent errors which may affect Grover's quantum algorithm and which can be characterized by the Hamiltonian H_d of equation (18). In the simple case of equal detunings, i.e. $\omega_1=\cdots=\omega_m\equiv \omega$ ,the error operator E reduces to the form

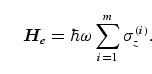$\begin{equation} {\bi H}_e = \hbar \omega \sum_{i=1}^m \sigma_z^{(i)}. \end{equation}$

(21)

It is easy to find highly degenerate error-free subspaces of this error operator. All states with a fixed number of ones and zeros constitute a degenerate eigenspace of H_e [34,35]. For an even number of qubits it is possible to find an error avoiding subspace with eigenvalue c = 0 so that

$\begin{equation} ({\bi H}_G + {\bi H}_e) \vert \psi \rangle = {\bi H} _G \vert \psi\rangle \end{equation}$

(22)

for all elements $\vert\psi\rangle$ of this subspace. For this purpose one is looking for quantum states with zero total spin. For four qubits, for example, this subspace is defined by the basis vectors $\vert011 \rangle$ , $\vert101 \rangle$ , $\vert110 \rangle$ , $\vert 1001 \rangle$ , $\vert 1010 \rangle$ and $\vert 1100 \rangle$ and involves all states with the same number of zeros and ones. Four of these states may be used as a basis for the state space of two logical qubits. For these eigenstates the error Hamiltonian H_e maps onto zero, e.g.

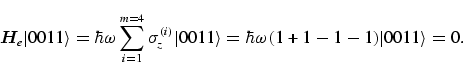$\begin{displaymath} {\bi H}_e \vert011\rangle = \hbar \omega \sum_{i=1}^{m=4} \s... ...1\rangle = \hbar \omega (1 + 1 - 1 - 1 ) \vert 0011\rangle = 0. \end{displaymath}$

This particular error avoiding code works ideally for equal detunings of all qubits from resonance. It is formed by quantum states which factorize in the computational basis. So it is expected that the encoding of quantum information and the implementation of quantum gates in this error-free subspace will be considerably easier than will that in cases in which the error avoiding codes involve entangled quantum states.

3.2. Implementation of quantum gates in an error-free subspace

To realize a quantum algorithm in an error-free subspace one has to implement the necessary quantum gates in such a way that they do not mix the error-free subspace with its orthogonal complement [36,37]. Consider two logical qubits, for example, which are encoded by four physical qubits. For this purpose one may choose the states $\vert011 \rangle$ , $\vert101 \rangle$ , $\vert110 \rangle$ and $\vert 1001 \rangle$ which have been mentioned in the previous subsection. This error avoiding code works ideally for stabilizing Grover's algorithm with respect to the error operator H_e of equation (21) provided that it is possible to realize the required unitary transformations, namely Hadamard transformations and the controlled phase inversions.

Consider as an example a Hadamard transformation which acts in a two-dimensional error avoiding subspace of this kind. Hence it is assumed that the two basis states of this error avoiding code are given by $\vert1\rangle$ and $\vert 10\rangle$ and that they involve two physical qubits. Thus, we are looking for a transformation which performs the mappings

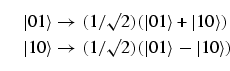$\begin{equation} \eqalign{ \vert1\rangle \to (1/\surd{2}) (\vert1\rangle + \vert... ...vert 10\rangle \to (1/\surd{2}) (\vert1\rangle - \vert 10\rangle)} \end{equation}$

(23)

and which does not mix the subspace spanned by $\vert1\rangle$ and $\vert 10\rangle$ with the orthogonal space spanned by the basis states $\vert0\rangle$ and $\vert 11\rangle$ . In matrix notation we are looking for a unitary matrix of the form

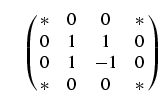$\begin{equation} \left(\matrix{\ast & 0 & 0 & \ast\cr 0 & 1 & 1 & 0\cr 0 & 1 & - 1 & 0\cr \ast & 0 & 0 & \ast}\right) \end{equation}$

(24)

with $\ast$ denoting arbitrary entries which ensure unitarity. Such a transformation can be achieved by the gate sequence $CNOT_{21} ({\bf 1}\otimes \otilde{H}^{(2)})CNOT_{21}$ with $\otilde{H}^{(2)} = -\mathrm{i} \sigma_y H^{(2)}$ . Here CNOT₂₁ is a controlled-not operation with the first qubit as the target and the second qubit as the control qubit and $\sigma_y$ is the Pauli matrix. Thus in matrix notation this relation yields

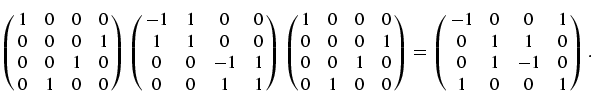$\begin{equation} \fl\left(\matrix{1 & 0 & 0 & 0 \cr 0 & 0 & 0 & 1 \cr 0 & 0 & 1 ... ...1 \cr 0 & 1 & 1 & 0 \cr 0 & 1 & - 1 & 0 \cr 1 & 0 & 0 & 1}\right). \end{equation}$

(25)

Obviously the final result does not mix the error avoiding subspace with its orthogonal complement. However, such a mixing might take place in the intermediate steps, depending on which set of universal quantum gates can be implemented. However, even in the worst possible case it suffices to ensure that the time spent by the quantum computer in the orthogonal complement of the error avoiding subspace is sufficiently small that the resulting errors can be neglected for all practical purposes. Under these circumstances it is expected that the implementation of quantum algorithms in error avoiding subspaces will be a powerful means for stabilizing quantum codes.

3.3. Code sizes of error avoiding quantum codes

In order to estimate the redundancy which has to be introduced for stabilizing a quantum algorithm by an error avoiding quantum code let us consider the particular example of section 3.1 in more detail. It has been argued that, in the case of coherent errors which can be characterized by the Hamiltonian of equation (21), an error avoiding quantum code can be constructed from basis states with equal numbers of ones and zeros. In order to minimize the redundancy it is desirable to maximize the dimension of the resulting error avoiding subspace. If one starts with m physical qubits, the dimension D(m,q) of the corresponding error avoiding subspace with q qubits in state $\vert 1\rangle$ and m - q qubits in state $\vert\rangle$ , for example, is given by

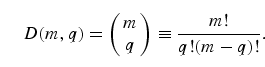$\begin{equation} D(m,q) = \left(\matrix{m\cr q}\right) \equiv\frac{m!}{q!(m-q)!}. \end{equation}$

(26)

From elementary properties of binomial coefficients it is clear that D(m,q) is maximum for q = m/2. Thus, for an even number of qubits m, the largest possible dimension of the resulting error avoiding subspace is given by

$\begin{equation} D(m,m/2) = \frac{m!}{[(m/2)!]^2} \to 2^m\left(\frac{2}{m\pi}\right)^{\!1/2}\tqs (m\gg 1). \end{equation}$

(27)

Thus, in this case it is possible to encode

$\begin{equation} l = {\rm log}_2 D(m,m/2) \to m - \frac{{\rm log}_2 m}{2} +{\rm log}_2[(2/\pi)^{1/2}]\tqs (m\gg 1) \end{equation}$

(28)

logical qubits with m physical ones. It is instructive to compare the redundancy of this error avoiding code described by equation (28) with the ones resulting from active error correcting quantum codes which saturate the quantum Hamming bound [13,25]. If one wants to correct arbitrary errors of maximum length t with a non-degenerate error correcting quantum code, the number of physical and logical qubits m and l must satisfy the so-called quantum Hamming bound [13,14,25], i.e.

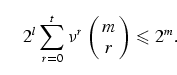$\begin{equation} 2^l \sum_{r=0}^{t} \nu^r \left(\matrix{m\cr r}\right) \leq 2^m. \end{equation}$

(29)

Here the length t of an error is the number of one-qubit errors which can be detected by a single measurement and which can thus be corrected; $\nu$ is the number of different one-qubit errors the code is able to correct. This inequality reflects the fact that, in a non-degenerate error correcting quantum code, the actions of various error operators on any of the logical qubits must lead to orthogonal quantum states. The dimension of the resulting Hilbert space described by the left-hand side of the inequality (29) has to be smaller than the dimensions of the Hilbert spaces of all physical qubits. For the detuning given by (21), there is only one error, i.e. $\nu = 1$ . Thus the number of logical qubits obtainable by a non-degenerate error correcting code of maximum length unity, i.e. t = 1, cannot be larger than

l_;SPMgt; = m - log₂(m+1).

(30)

On comparing equation (28) with equation (30), one realizes that the redundancy of this particular error avoiding quantum code is smaller than that of any non-degenerate error correcting code saturating the Hamming bound, i.e.

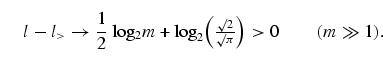$\begin{equation} l - l_\gt \to \frac{1}{2}$~log$_2 m + {\rm log}_2\bigg(\frac{\surd 2}{\surd \pi}\bigg) \gt 0\tqs (m\gg 1). \end{equation}$

(31)

For codes with maximum lengths larger than 1, we obtain $l_\gt \approx m - t$ log₂ m (see figure 6). An error avoiding code may be considered as an error correcting code which is capable of correcting errors of infinite length, i.e. $t \to \infty$ [38]. In addition, its redundancy is smaller than that of a non-degenerate code which is able to correct only errors of distance t = 1.

$\begin{figure} \hspace{6pc} \epsfxsize=20pc \epsfbox {1302206.eps} \end{figure}$

Figure 6. The maximum number of logical qubits l versus the number of physical qubits m for the error avoiding quantum codes which are capable of stabilizing the error operator of equation (21) (diamonds) (compare with equation (28)). The corresponding relation l_>(m) obtained from equation (29) characterizing the quantum Hamming bound is indicated by stars (t = 1), triangles (t = 2) and boxes (t = 3).

4. Numerical examples

In the previous section we have developed an error avoiding quantum code which is capable of correcting coherent errors. These errors were assumed to be caused by systematic detunings of the physical qubits of the quantum computer from the frequency of the laser pulses implementing the action of the quantum gates. This error avoiding quantum code works perfectly provided that all physical qubits are detuned from the frequency of these laser pulses by the same amount. However, in realistic situations this case is hardly ever realized. For the realistic assumption of unequal detunings in general the eigenstates of H_d are non-degenerate so that it is not possible to construct a perfect error avoiding quantum code. Therefore the practical question of whether the presented error avoiding quantum code of section 3 is still useful for stabilizing quantum algorithms against arbitrary systematic detunings arises. A first general result in this direction was derived by Lidar et al [26]. They have shown in a perturbative analysis that any error avoiding quantum code is stable against weak perturbations. However, so far questions concerning the maximal range of validity of an error avoiding quantum code have not been addressed.

$\begin{figure} \hspace{6pc} \epsfxsize=20pc \epsfbox {1302207.eps} \end{figure}$

Figure 7. The probability of finding the quantum computer in the sought state $\vert x_0\rangle$ after $n = t/\tau$ iterations: ideal dynamics without detunings for six qubits (broken line); with detunings and without error avoiding encoding for eight qubits (dotted line); and with detunings and with error avoiding encoding using eight physical qubits which can encode the quantum information of six logical qubits (full line). For the latter two cases the magnitudes of the detunings $\omega_i$ of the eight qubits which determine the error operator of equation (18) are given by $\omega_i \tau/\langle v\vert s\rangle = 0.920~65$ , 1.1436, 0.714 49, 1.395 66, 1.297 07, 0.701 49, 1.191 95 and 1.003 43.

The dynamics of Grover's algorithm in the presence of arbitrary detunings is depicted in figure 7. The broken line represents the ideal dynamics in the absence of detunings for the case of six qubits evaluated from the Hamiltonian of equation (16). The characteristic Rabi oscillations are clearly apparent. The corresponding dynamics for eight qubits in the presence of arbitrarily chosen detunings is depicted by the dotted line in figure 7. It is apparent that, in this case, a quantum search for the state $\vert x_0\rangle$ is not at all successful. However, as is apparent from the full line in figure 7, encoding the quantum information by the error avoiding code of section 3 improves the performance considerably. Despite the fact that this error avoiding code has not been designed for these detunings, it almost succeeds at finding the sought quantum state $\vert x_0\rangle$ after a number of iterations which is close to that of the ideal case (compare with equation (14)). Similar stability properties of error avoiding codes have been observed by Lidar et al [26].

In order to obtain more insight into the stabilizing properties of this error avoiding code, let us investigate the probability of success in the presence of arbitrary detunings in more detail. For this purpose we consider eight physical qubits whose detunings $\omega_i$ are distributed randomly according to a normal distribution. According to figure 6 these eight physical qubits are capable of encoding six logical qubits. In figure 8 the average value of the maximum probability of finding the quantum computer in the sought state $\vert x_0\rangle$ for various values of the variance of the randomly chosen detunings is depicted. The lower sequence of dots (stars) refers to Grover's algorithms without error avoiding encoding and the upper sequence of points (diamonds) refers to error avoiding encoding according to section 3. It is apparent that error avoiding encoding is very successful as long as the difference between the detunings of the qubits is sufficiently small. Only in extreme cases in which these differences become comparable to the typical magnitudes of the detunings is this type of error avoiding code no longer capable of stabilizing Grover's algorithm in a satisfactory way.

$\begin{figure} \hspace{6pc} \epsfxsize=20pc \epsfbox {1302208.eps} \end{figure}$

Figure 8. The average maximum probability of success for Grover's algorithm with eight qubits in the presence of randomly chosen detunings: with error avoiding encoding according to section 3 (diamonds); and without error avoiding encoding (stars). The detunings $\omega_i$ of the eight physical qubits were chosen randomly according to a normal distribution with mean value $\ovrline{\omega}=0.5\langle v\vert s\rangle/\tau$ . The corresponding variance $\sigma$ of these detunings is plotted on the x-axis in units of the mean value $\ovrline{\omega}$ .

5. Summary and conclusions

It has been demonstrated that error avoiding quantum codes may offer efficient methods for stabilizing quantum codes dynamically against errors. As a particular example we discussed the stabilization of Grover's quantum search algorithm against coherent errors which may arise from systematic detunings of the physical qubits from the frequency of the light pulses implementing the quantum gates. Even though originally the error avoiding quantum code had been constructed for the special case of equal detunings of all the qubits, it has been shown that it is also capable of stabilizing this quantum algorithm to a satisfactory degree in other non-ideal cases well beyond the perturbative regime. The error avoiding quantum code considered consists solely of quantum states which are factorizable in the computational basis. This may offer advantages insofar as the implementation of the necessary quantum gates in this error-free subspace is concerned. Although the stabilizing ability of error avoiding quantum codes has been demonstrated for one particular quantum code and one particular class of coherent errors only, it is expected that similar capabilities will also be found in more general cases which may also involve incoherent errors.

After the submission of this paper we became aware of a preprint by Kempe et al [39] concerning quantum computation on decoherence-free subspaces. In this preprint some of the issues addressed in section 3.2 are also considered.

Acknowledgments

This work was supported by the DFG within the SPP `Quanteninformationsverarbeitung'. Stimulating discussions with Thomas Beth, Markus Grassl and Dominik Janzing are acknowledged. AD acknowledges support by the DAAD.

References

[1]: Feynman R P 1982 Int. J. Theor. Phys. 21 467-88
Inspec Abstract | Order from Infotrieve
[2]: Shor W 1994 Proc. 35th Ann. Symp. on Foundations of Computer Science ed S Goldwasser (Los Alamitos, CA: IEEE Computer Society) p 124
[3]: Grover L K 1997 Phys. Rev. Lett. 79 325
CrossRef Link | Inspec Abstract | ChemPort Abstract | Order from Infotrieve
[4]: Grover L K 1998 Phys. Rev. Lett. 80 4329
CrossRef Link | Inspec Abstract | ChemPort Abstract | Order from Infotrieve
[5]: Cirac J I and Zoller P 1995 Phys. Rev. Lett. 74 4091
CrossRef Link | Inspec Abstract | ChemPort Abstract | PubMed Abstract | Order from Infotrieve
[6]: Gershenfeld N and Chuang I 1997 Science 275 350
CrossRef Link | Inspec Abstract | MathSciNet Review | ChemPort Abstract | PubMed Abstract | Order from Infotrieve
[7]: Pellizzari T, Gardiner S A, Cirac J I and Zoller P 1995 Phys. Rev. Lett. 75 3788
CrossRef Link | Inspec Abstract | ChemPort Abstract | PubMed Abstract | Order from Infotrieve
[8]: Boyer M, Brassard G, Hoyer P and Tapp A 1998 Fortschr. Phys. 46 493
CrossRef Link | Inspec Abstract | Link to SwetsWise | Order from Infotrieve
[9]: Chuang I L, Gershenfeld N and Kubinec M 1998 Phys. Rev. Lett. 80 3408
CrossRef Link | Inspec Abstract | ChemPort Abstract | Order from Infotrieve
[10]: Miquel C, Paz J P and Zurek W H 1997 Phys. Rev. Lett. 78 3971
CrossRef Link | Inspec Abstract | MathSciNet Review | ChemPort Abstract | Order from Infotrieve
[11]: Shor P W 1995 Phys. Rev. A 52 R2493
CrossRef Link | Inspec Abstract | ChemPort Abstract | Order from Infotrieve
[12]: Calderbank A R and Shor P W 1996 Phys. Rev. A 54 1098
CrossRef Link | Order from Infotrieve
[13]: Gottesman D 1996 Phys. Rev. A 54 1862
CrossRef Link | MathSciNet Review | Order from Infotrieve
[14]: Laflamme R, Miquel C, Paz J P and Zurek W H 1996 Phys. Rev. Lett. 77 198
CrossRef Link | Inspec Abstract | ChemPort Abstract | PubMed Abstract | Order from Infotrieve
[15]: Steane A M 1996 Phys. Rev. Lett. 77 793
CrossRef Link | Inspec Abstract | MathSciNet Review | ChemPort Abstract | PubMed Abstract | Order from Infotrieve
[16]: Bennett C H, Di Vincenzo D P, Smolin J A and Wootters W K 1996 Phys. Rev. A 54 3824
CrossRef Link | Order from Infotrieve
[17]: Kitaev A Yu 1996 Russ. Math. Surveys 53 1191
Order from Infotrieve
[18]: Knill E and Laflamme R 1997 Phys. Rev. A 55 900
CrossRef Link | MathSciNet Review | Order from Infotrieve
[19]: Steane A 1998 Rep. Prog. Phys. 61 117-73
IOP Article
[20]: Duan L M and Guo G C 1997 Phys. Rev. Lett. 79 1953
CrossRef Link | Inspec Abstract | ChemPort Abstract | Order from Infotrieve
[21]: Zanardi P and Rasetti M 1997 Phys. Rev. Lett. 79 3306
CrossRef Link | Inspec Abstract | ChemPort Abstract | Order from Infotrieve
[22]: Zanardi P 1998 Phys. Rev. A 57 3276
CrossRef Link | Order from Infotrieve
[23]: Zanardi P 1999 Phys. Rev. A 60 R729
CrossRef Link | Inspec Abstract | ChemPort Abstract | Order from Infotrieve
[24]: Lidar D A, Chuang I L and Whaley K B 1998 Phys. Rev. Lett. 81 2594
CrossRef Link | Inspec Abstract | ChemPort Abstract | Order from Infotrieve
[25]: Welsh D 1988 Codes and Cryptography (Oxford: Clarendon)
[26]: Lidar D A, Bacon D and Whaley K B 1999 Phys. Rev. A 60 1944
CrossRef Link | Order from Infotrieve
[27]: Zalka C 1999 Phys. Rev. A 60 2746
CrossRef Link | Order from Infotrieve
[28]: Biham E, Biham O, Biron D, Grassl M and Lidar D A 1999 Phys. Rev. A 60 2742
CrossRef Link | Order from Infotrieve
[29]: Gingrich R M, Williams C P and Cerf N J 2000 Phys. Rev. A 61 052313
Order from Infotrieve
[30]: Fahri E and Gutmann S 1998 Phys. Rev. A 57 2403
CrossRef Link | Order from Infotrieve
[31]: Schulman L 1981 Techniques and Applications of Path Integration (New York: Wiley)
[32]: Averbukh I Sh and Perelman N F 1989 Phys. Lett. A 139 449
CrossRef Link | Inspec Abstract | Order from Infotrieve
[33]: Pellizzari T, Beth Th, Grassl M and Müller-Quade J 1996 Phys. Rev. A 54 2698
CrossRef Link | Order from Infotrieve
[34]: Lidar D A, Bacon D and Whaley K B 1999 Phys. Rev. Lett. 82 4556
CrossRef Link | Inspec Abstract | ChemPort Abstract | Order from Infotrieve
[35]: Duan L M and Guo G C 1998 Phys. Rev. A 57 737
CrossRef Link | Order from Infotrieve
[36]: Bacon D, Kempe J, Lidar D A and Whaley K B 1999 Preprint lanl e-print quant-ph/9909058
Preprint at arXiv.org
[37]: Beige A, Braun D and Knight P 1999 Preprint lanl e-print quant-ph/9912004
Preprint at arXiv.org
[38]: Knill E, Laflamme R and Viola C 2000 Phys. Rev. Lett. 84 2525
CrossRef Link | Inspec Abstract | ChemPort Abstract | PubMed Abstract | Order from Infotrieve
[39]: Kempe J, Bacon D, Lidar D A and Whaley K B 2000 Preprint lanl e-print quant-ph/0004064
Preprint at arXiv.org

This volume

| Abstract

Full Search
Help


Author: Vol/Year: Issue/Month: Page/Article No: