Axially Deformed Solution of the Skyrme-Hartree-Fock-Bogolyubov Equations using The Transformed Harmonic Oscillator Basis.

The program HFBTHO (v1.66p)

M.V. Stoitsov$^{{a-d,}}$, J. Dobaczewski$^{{a-c,e}}$, W. Nazarewicz$^{{a,b,e}}$, P. Ring$^{{f}}$

$^{{a}}$Department of Physics and Astronomy, University of Tennessee, Knoxville, TN 37996, USA

$^{{b}}$Physics Division, Oak Ridge National Laboratory, P.O.B. 2008, Oak Ridge, TN 37831, USA

$^{{c}}$Joint Institute for Heavy Ion Research, Oak Ridge, TN 37831, USA

$^{{d}}$Institute of Nuclear Research and Nuclear Energy, Bulgarian Academy of Sciences, Sofia, Bulgaria

$^{{e}}$Institute of Theoretical Physics, Warsaw University, ul.Hoza 69, 00-681 Warsaw, Poland

$^{{f}}$Physics Department, Technical University Munich, Garching, Germany

Abstract:

We describe the program HFBTHO for axially deformed configurational Hartree-Fock-Bogoliubov calculations with Skyrme-forces and zero-range pairing interaction using Harmonic-Oscillator and/or Transformed Harmonic-Oscillator states. The particle-number symmetry is approximately restored using the Lipkin-Nogami prescription, followed by an exact particle number projection after the variation. The program can be used in a variety of applications, including systematic studies of wide ranges of nuclei, both spherical and axially deformed, extending all the way out to nucleon drip lines.

Program Summary

Title of the program: HFBTHO (v1.66p)

Catalogue number:

Program obtainable from: CPC Program Library, Queen's University of Belfast, N. Ireland

Program summary URL:

Licensing provisions: none

Computers on which the program has been tested: Pentium-III, Pentium-IV, AMD-Athlon, IBM Power 3, IBM Power 4, Intel Xeon

Operating systems: LINUX, Windows

Programming language used: FORTRAN-95

Memory required to execute with typical data: 59 MB when using 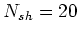$N_{sh}=20$

No. of bits in a word: 64

No. of processors used: 1

Has the code been vectorized?: No

No. of bytes in distributed program, including test data, etc.:

No. of lines in distributed program: 7876 lines

Nature of physical problem: Solution of self-consistent mean-field equations for weakly bound paired nuclei requires correct description of asymptotic properties of nuclear quasiparticle wave functions. In the present implementation, this is achieved by using the single-particle wave functions of the Transformed Harmonic Oscillator, which allows for an accurate description of deformation effects and pairing correlations in nuclei arbitrarily close to the particle drip lines.

Method of solution: The program uses axial Transformed Harmonic Oscillator single-particle basis to expand quasiparticle wave functions. It iteratively diagonalizes the Hartree-Fock-Bogolyubov Hamiltonian based on the Skyrme forces and zero-range pairing interaction until the self-consistent solution is achieved.

Restrictions on the complexity of the problem: Axial-, time-reversal-, and space-inversion symmetries are assumed. Only quasiparticle vacua of even-even nuclei can be calculated.

Typical running time: 4 seconds per iteration on an Intel Xeon 2.8 GHz processor when using 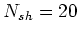$N_{sh}=20$

Unusual features of the program: none

PACS: 07.05.T, 21.60.-n, 21.60.Jz

Keywords: Hartree-Fock; Hartree-Fock-Bogolyubov; Nuclear many-body problem; Skyrme interaction; Self-consistent mean-field; Quadrupole deformation; Constrained calculations; Energy surface; Pairing; Particle number projection; Nuclear radii; Quasiparticle spectra; Harmonic oscillator; Coulomb field