The main differences between the results of coordinate-space HFB calculations and those from configuration-space HFB+HO calculations can be seen in plots of the corresponding local density distributions. A typical example is shown in Fig. 1, where the densities and their logarithmic derivatives from coordinate-space HFB calculations (solid lines) are compared with those from a configurational HFB+HO calculation. Although the calculations were done for a specific spherical nucleus and Skyrme interaction, the features exhibited are generic. Note that the coordinate-space HFB calculations were carried out in a box of 30fm, so that the logarithmic derivative of the density obtained in that calculation shows a sudden drop near the box edge.
Invariably, the logarithmic derivative
![]() associated with the coordinate-space HFB solution shows a
well-defined minimum near some point
associated with the coordinate-space HFB solution shows a
well-defined minimum near some point
![]() in the
asymptotic region, after which it smoothly approaches a constant
value
in the
asymptotic region, after which it smoothly approaches a constant
value ![]() , where
, where
Moreover, the HFB value of the density decay constant
![]() =2
=2![]() , when calculated from Eq. (19), is also
correctly reproduced by the HFB+HO results. It is not possible to
distinguish between the values of
, when calculated from Eq. (19), is also
correctly reproduced by the HFB+HO results. It is not possible to
distinguish between the values of ![]() that emerge from the
coordinate-space and harmonic-oscillator HFB calculations, both
values being shown by the same line in the upper panel of
Fig. 1.
that emerge from the
coordinate-space and harmonic-oscillator HFB calculations, both
values being shown by the same line in the upper panel of
Fig. 1.
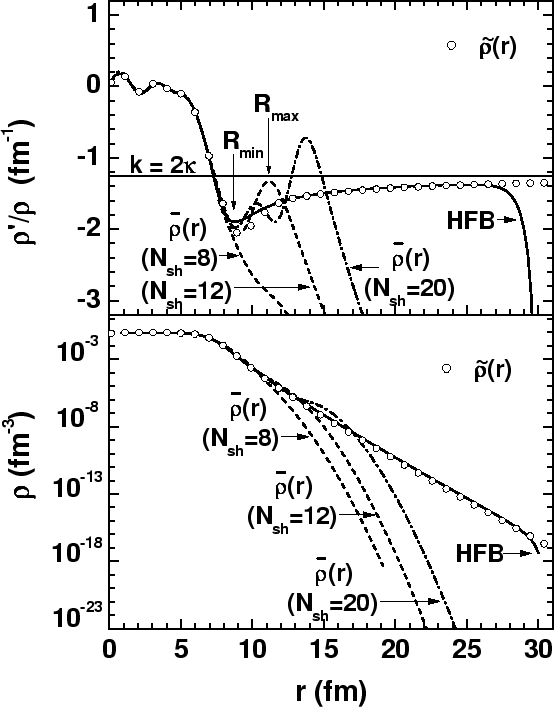 |
Soon beyond the point ![]() , the HFB+HO density begins
to deviate dramatically from that obtained in the coordinate-space
calculation. For relatively small numbers of harmonic oscillator
shells
, the HFB+HO density begins
to deviate dramatically from that obtained in the coordinate-space
calculation. For relatively small numbers of harmonic oscillator
shells ![]() , the logarithmic derivative of the HFB+HO
density goes asymptotically to zero following the gaussian
behavior of the harmonic oscillator basis. The resulting HFB+HO
density does not develop a minimum around the point
, the logarithmic derivative of the HFB+HO
density goes asymptotically to zero following the gaussian
behavior of the harmonic oscillator basis. The resulting HFB+HO
density does not develop a minimum around the point ![]() , as seen from the
, as seen from the
![]() curve shown in the upper
panel of Fig. 1. When the number of harmonic oscillator
shells
curve shown in the upper
panel of Fig. 1. When the number of harmonic oscillator
shells ![]() increases, the HFB+HO solution tries to
capture the correct density asymptotics. Due to the gaussian
asymptotic of the basis, however, the logarithmic derivative of
the HFB+HO density only develops oscillations around the exact
solution (see the
increases, the HFB+HO solution tries to
capture the correct density asymptotics. Due to the gaussian
asymptotic of the basis, however, the logarithmic derivative of
the HFB+HO density only develops oscillations around the exact
solution (see the
![]() and
and ![]() curves in the upper
panel of Fig. 1). As a result, the logarithmic derivative
of the HFB+HO density is very close to the coordinate-space result
around the mid point
curves in the upper
panel of Fig. 1). As a result, the logarithmic derivative
of the HFB+HO density is very close to the coordinate-space result
around the mid point
![]() , where
, where
![]() is the position of the first maximum of the
logarithmic derivative after
is the position of the first maximum of the
logarithmic derivative after ![]() .
.
In summary, the following HFB+HO quantities agree with the
coordinate-space HFB results: (i) the value of the density
decay constant ![]() ; (ii) the local density up to the point
; (ii) the local density up to the point
![]() where the logarithmic derivative
where the logarithmic derivative
![]() shows a clearly-defined minimum; (iii) the actual
value of this point
shows a clearly-defined minimum; (iii) the actual
value of this point
![]() ; (iv) the value of the
logarithmic derivative of the density at the point
; (iv) the value of the
logarithmic derivative of the density at the point ![]() defined
above. In fact, the last of the above is not established nearly as
firmly as the first three; nevertheless, we shall make use of it
in developing our new formulation of the HFB+THO method.
defined
above. In fact, the last of the above is not established nearly as
firmly as the first three; nevertheless, we shall make use of it
in developing our new formulation of the HFB+THO method.
Beyond the point ![]() , the HFB+HO solution fails to capture the
physics of the coordinate-space results, especially in the far
asymptotic region. It is this incorrect large-
, the HFB+HO solution fails to capture the
physics of the coordinate-space results, especially in the far
asymptotic region. It is this incorrect large-![]() behavior that we
now try to cure by introducing the THO basis.
behavior that we
now try to cure by introducing the THO basis.