The simplest route to the HFB theory is to employ
the variational principle to a two-body Hamiltonian using
Thouless states (6) as trial wave functions.
The variation of the average energy with respect to the antisymmetric matrix ![]() results in the HFB equation in the matrix representation,
results in the HFB equation in the matrix representation,
![]() , or explicitly,
, or explicitly,
The matrices ![]() and
and ![]() are referred to as the HFB Hamiltonian
and Bogoliubov transformation, respectively, and columns of
are referred to as the HFB Hamiltonian
and Bogoliubov transformation, respectively, and columns of ![]() (eigenstates of
(eigenstates of ![]() ) are vectors of quasiparticle states. The HFB
equation (7) possesses the quasiparticle-quasihole
symmetry. Namely, for each quasiparticle state
) are vectors of quasiparticle states. The HFB
equation (7) possesses the quasiparticle-quasihole
symmetry. Namely, for each quasiparticle state
![]() (the
(the
![]() -th column of
-th column of ![]() ) and energy
) and energy ![]() there exists
a quasihole state
there exists
a quasihole state
![]() of opposite energy
of opposite energy ![]() ,
,
The HFB equation (7) is also valid in a more general
case, when the total energy is not equal to the average of any many-body Hamiltonian.
Within the DFT, it stems from the
minimization of the binding energy given by an EDF
![]() ,
subject to the condition of the generalized density
matrix being projective, that is,
,
subject to the condition of the generalized density
matrix being projective, that is,
![]() for
for
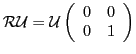 ;
the Thouless state
;
the Thouless state
Unrestricted variations of the EDF are not meaningful.
Indeed, since Thouless states (3) are mixtures of components
with different particle numbers, absolute minima will usually correspond to
average particle numbers that are unrelated to those one would like
to describe.
In particular, for self-bound systems governed by attractive two-body
forces (nuclei), by adding more and more particles one could infinitely
decrease the total energy of the system. Therefore, only constrained variations
make sense, that is, one has to minimize not the total energy
![]() , but the so-called Routhian,
, but the so-called Routhian,
![]() ,
where
,
where ![]() is a suitably chosen penalty functional,
ensuring that the minimum appears at prescribed average values
of one-body operators. In particular, the average total number of
particles can be constrained by
is a suitably chosen penalty functional,
ensuring that the minimum appears at prescribed average values
of one-body operators. In particular, the average total number of
particles can be constrained by
![]() (linear constraint) or
(linear constraint) or
![]() (quadratic
constraint),[16,17] where
(quadratic
constraint),[16,17] where ![]() becomes the Fermi
energy corresponding to
becomes the Fermi
energy corresponding to ![]() fermions.
fermions.
For different systems and for different applications, various
constraints
![]() can be implemented; for example, in
nuclei one can simultaneously constrain numbers of protons and
neutrons, as well as multipole moments of matter or charge
distributions. When the total energy is a concave function of
relevant one-body average values, quadratic constraints are
mandatory[16,17]. The minimization of
can be implemented; for example, in
nuclei one can simultaneously constrain numbers of protons and
neutrons, as well as multipole moments of matter or charge
distributions. When the total energy is a concave function of
relevant one-body average values, quadratic constraints are
mandatory[16,17]. The minimization of
![]() requires solving the HFB equation
for the quasiparticle Routhian
requires solving the HFB equation
for the quasiparticle Routhian ![]() , which, for the simplest
case of the constraint on the total particle number, reads
, which, for the simplest
case of the constraint on the total particle number, reads
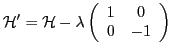 .
.
Finally, let us mention that in the coordinate space-spin(-isospin)
representation, the HFB equation (7) acquires
particularly interesting form, which in condensed matter and atomic
literature is called Bogoliubov-de Gennes equation[4].
In the coordinate representation, quasiparticle vectors become
two-component wave functions, which - in finite systems - acquire
specific asymptotic properties[18,19,20,21]
determining the asymptotic behavior of local densities.
The quasiparticle energy spectrum of HFB contains discrete bound
states, resonances, and non-resonant continuum states. As illustrated
in Fig. 1, the bound HFB solutions exist only in the
energy region
![]() . The quasiparticle continuum
with
. The quasiparticle continuum
with
![]() consists of non-resonant continuum and
quasiparticle resonances, see Sec. 6.
consists of non-resonant continuum and
quasiparticle resonances, see Sec. 6.
![\includegraphics[width=0.50\textwidth]{HFBspectrum.eps}](img81.png) |