The no-core configuration-interaction model
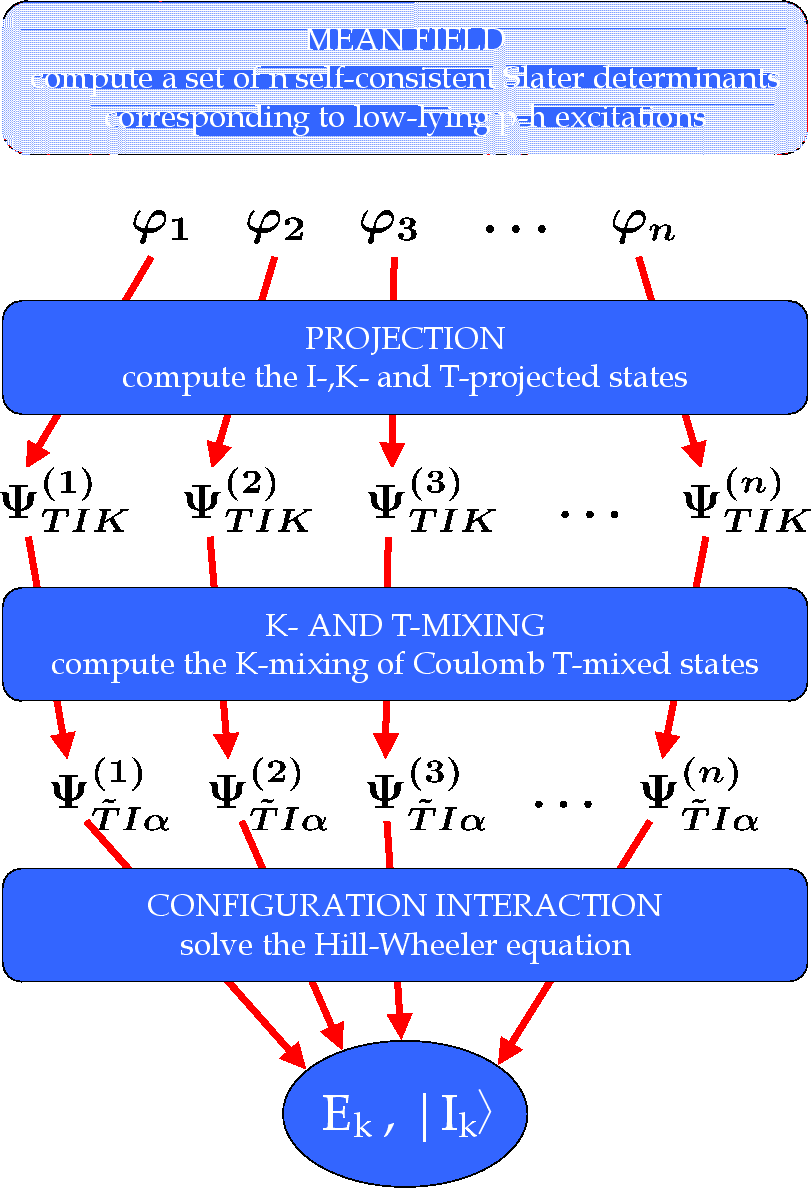
Figure 1:
(Color online) Computational scheme of the NCCI model. See text for
details.
|
 |
The static model developed in our previous works [15,21]
involved the isospin and angular momentum projections (after variation) of a single Slater
determinant, followed by a rediagonalization of the Coulomb force, so as to account properly for
the isospin mixing. Here we extend the model towards a variant, in which
we allow for a mixing of states projected from different low-lying
(multi)particle-(multi)hole Slater determinants 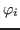 with the mixing matrix elements derived
from the same Hamiltonian that is used to calculate them.
with the mixing matrix elements derived
from the same Hamiltonian that is used to calculate them.
The computational scheme of our NCCI model is sketched in
Fig. 1. It proceeds in four major steps:
- First, a set of relevant low-lying (multi)particle-(multi)hole HF
states
 is calculated along with their HF energies
is calculated along with their HF energies
 . States
. States
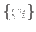 form a subspace of
reference states for subsequent projections.
form a subspace of
reference states for subsequent projections.
- Second, the projection techniques are applied to the set of
reference states
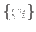 , so as to determine the family of
states
, so as to determine the family of
states
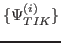 having good isospin
having good isospin 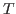 , angular
momentum
, angular
momentum 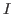 , and angular-momentum projection on the intrinsic axis
, and angular-momentum projection on the intrinsic axis
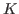 .
.
- Third, states
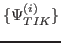 are mixed, so as to properly
take into account the
are mixed, so as to properly
take into account the 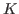 mixing and Coulomb isospin mixing - this
gives the set of good angular-momentum states
mixing and Coulomb isospin mixing - this
gives the set of good angular-momentum states
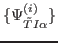 of
the static model [14,15]. Here we label them with the
dominating values of the isospin,
of
the static model [14,15]. Here we label them with the
dominating values of the isospin, 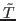 , and auxiliary quantum
numbers
, and auxiliary quantum
numbers 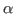 . Note that in this step, the mixing is performed
for each configuration
. Note that in this step, the mixing is performed
for each configuration 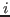 separately (the static model).
separately (the static model).
- Finally, the results of the dynamic model correspond to mixing
non-orthogonal states
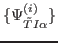 for all
configurations
for all
configurations 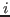 , and for all values of
, and for all values of 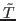 and
and 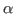 .
This is performed by solving the Hill-Wheeler equation
.
This is performed by solving the Hill-Wheeler equation
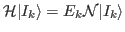 [22] in the
collective space spanned by the natural states
corresponding to sufficiently large eigenvalues of the norm matrix
[22] in the
collective space spanned by the natural states
corresponding to sufficiently large eigenvalues of the norm matrix
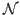 . This is the same technique that is used in the code to handle
the
. This is the same technique that is used in the code to handle
the 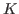 -mixing alone. The method is described in details in
Ref. [23].
-mixing alone. The method is described in details in
Ref. [23].
We note here that all wave functions considered above correspond to
good neutron (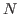 ), and proton (
), and proton (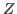 ) numbers, and thus to a good
third component of the isospin,
) numbers, and thus to a good
third component of the isospin,
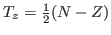 . We also note that
the configuration interaction, which is taken into account in the
last step, could have also equivalently been performed by directly
mixing the projected states
. We also note that
the configuration interaction, which is taken into account in the
last step, could have also equivalently been performed by directly
mixing the projected states
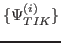 . The procedure
outlined above simply aims to obtain separately the results of the
static and dynamic model. The NCCI calculations discussed below were
performed using a new version of the HFODD solver [24],
which was equipped with the NCCI module. This new implementation was
based on the previous versions of the
code [23,25,26].
. The procedure
outlined above simply aims to obtain separately the results of the
static and dynamic model. The NCCI calculations discussed below were
performed using a new version of the HFODD solver [24],
which was equipped with the NCCI module. This new implementation was
based on the previous versions of the
code [23,25,26].
Numerical stability of the method depends on necessary truncations
of the model space. In this work, numerically unstable solutions are
removed by truncating the natural states corresponding to
small eigenvalues of the norm matrix 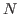 . It means that only the
natural states corresponding to the eigenvalues of the norm matrix
that are larger than certain externally provided cut-off parameter
. It means that only the
natural states corresponding to the eigenvalues of the norm matrix
that are larger than certain externally provided cut-off parameter
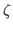 are used to built the so-called collective space.
Although such a truncation procedure gives reliable values of the
energy, a full stability of the method still requires further
studies. Other methods, e.g., based on truncating high-energy
states
are used to built the so-called collective space.
Although such a truncation procedure gives reliable values of the
energy, a full stability of the method still requires further
studies. Other methods, e.g., based on truncating high-energy
states
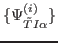 , or combined methods
involving both truncations simultaneously, need to be studied as
well.
, or combined methods
involving both truncations simultaneously, need to be studied as
well.
Jacek Dobaczewski
2016-03-05
![]() with the mixing matrix elements derived
from the same Hamiltonian that is used to calculate them.
with the mixing matrix elements derived
from the same Hamiltonian that is used to calculate them.
![]() . It means that only the
natural states corresponding to the eigenvalues of the norm matrix
that are larger than certain externally provided cut-off parameter
. It means that only the
natural states corresponding to the eigenvalues of the norm matrix
that are larger than certain externally provided cut-off parameter
![]() are used to built the so-called collective space.
Although such a truncation procedure gives reliable values of the
energy, a full stability of the method still requires further
studies. Other methods, e.g., based on truncating high-energy
states
are used to built the so-called collective space.
Although such a truncation procedure gives reliable values of the
energy, a full stability of the method still requires further
studies. Other methods, e.g., based on truncating high-energy
states
![]() , or combined methods
involving both truncations simultaneously, need to be studied as
well.
, or combined methods
involving both truncations simultaneously, need to be studied as
well.