Next: Low-energy spectra of selected Up: No-core configuration-interaction model for Previous: The no-core configuration-interaction model
In this section we present results obtained within the NCCI model,
which pertain to removing the uncertainty related to ambiguities in
the shape-current orientation.
Similar to our previous applications
within the static model, the ground-states (g.s.) of even-even
nuclei,
![]() , are approximated by
the Coulomb
, are approximated by
the Coulomb ![]() -mixed states,
-mixed states,
 |
(1) |
Within our dynamic model, the corresponding isobaric analogues in
![]() odd-odd nuclei,
odd-odd nuclei,
![]() , were
approximated by
, were
approximated by
For odd-odd nuclei, mixing coefficients
![]() in
Eq. (2) were determined by solving the Hill-Wheeler
equation. In the mixing calculations, we only included states
in
Eq. (2) were determined by solving the Hill-Wheeler
equation. In the mixing calculations, we only included states
![]() with dominating isospins of
with dominating isospins of
![]() and 2, that is, the Hill-Wheeler equation was solved
in the space of six or nine states for axial and triaxial states,
respectively. We recall that each of states
and 2, that is, the Hill-Wheeler equation was solved
in the space of six or nine states for axial and triaxial states,
respectively. We recall that each of states
![]() contains all Coulomb-mixed good-
contains all Coulomb-mixed good-![]() components
components
![]() .
.
The three states corresponding to a given dominating isospin are
linearly dependent. One may therefore argue that the physical
subspace of the ![]() states should be three dimensional. In the
calculations, all six or nine eigenvalues of the norm matrix
states should be three dimensional. In the
calculations, all six or nine eigenvalues of the norm matrix ![]() are
nonzero, but the linear dependence of the reference states is clearly
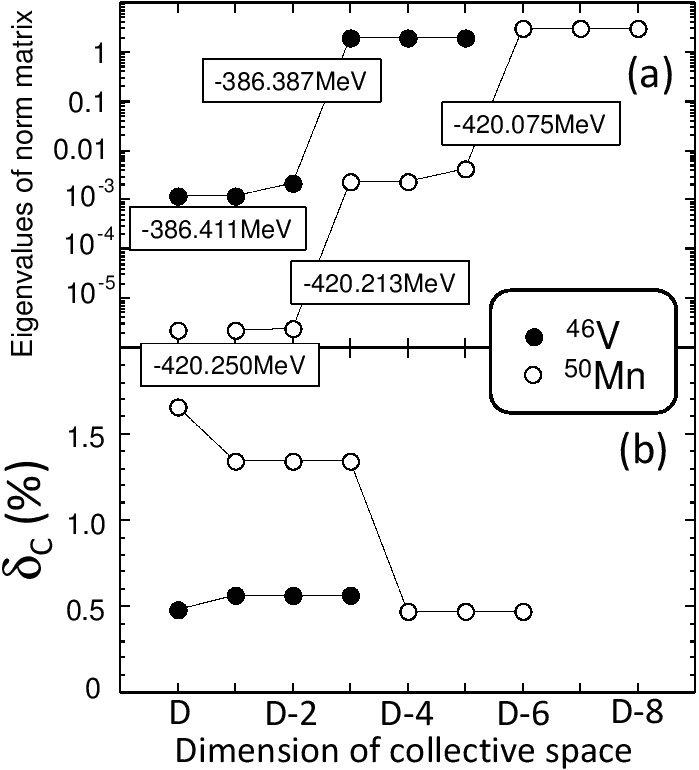
reflected in the pattern they form. For two representative examples
of axial (
are
nonzero, but the linear dependence of the reference states is clearly
reflected in the pattern they form. For two representative examples
of axial (![]() V) and triaxial (
V) and triaxial (![]() Mn) nuclei, this is depicted
in Fig. 2. Note, that the eigenvalues group into two or
three sets, each consisting of three similar eigenvalues.
Note also, that the differences between the sets are large, reaching
three-four orders of magnitude.
Lower part of the figure illustrates dependence of the calculated
ISB corrections,
Mn) nuclei, this is depicted
in Fig. 2. Note, that the eigenvalues group into two or
three sets, each consisting of three similar eigenvalues.
Note also, that the differences between the sets are large, reaching
three-four orders of magnitude.
Lower part of the figure illustrates dependence of the calculated
ISB corrections,
![]() , on a number of the collective states
retained in the mixing. As shown, the calculated corrections are becoming stable
within a subspace consisting five (or less) highest-norm
states. Following this result, we have decided to retain in the
mixing calculations only three collective states built upon the three
eigenvectors of the norm matrix corresponding to the largest
eigenvalues.
, on a number of the collective states
retained in the mixing. As shown, the calculated corrections are becoming stable
within a subspace consisting five (or less) highest-norm
states. Following this result, we have decided to retain in the
mixing calculations only three collective states built upon the three
eigenvectors of the norm matrix corresponding to the largest
eigenvalues.
 |
Based on this methodology, we calculated the set of the superallowed
transitions, which are collected in Tables 1 and
2. Table 1 shows the empirical
![]() values, calculated ISB corrections, and so-called
nucleus-independent reduced lifetimes,
values, calculated ISB corrections, and so-called
nucleus-independent reduced lifetimes,
Except for transitions ![]() O
O
![]()
![]() N and
N and
![]() Sc
Sc
![]()
![]() Ca, all ISB corrections were
calculated using the prescription sketched above. For the decay
of a spherical nucleus
Ca, all ISB corrections were
calculated using the prescription sketched above. For the decay
of a spherical nucleus ![]() O, the reference state is uniquely
defined and thus the mixing of orientations was not necessary, whereas
for that of
O, the reference state is uniquely
defined and thus the mixing of orientations was not necessary, whereas
for that of ![]() Sc, an ambiguity of choosing its reference state
is not related to the shape-current orientation. For both cases, the
values and errors of
Sc, an ambiguity of choosing its reference state
is not related to the shape-current orientation. For both cases, the
values and errors of
![]() were taken from
Ref. [15]. For the remaining cases, to account for
uncertainties related to the basis size and collective-space cut-off,
we assumed an error of 15%. This is larger than the 10%
uncertainties related to the basis size only, which were assumed
in Ref. [15].
were taken from
Ref. [15]. For the remaining cases, to account for
uncertainties related to the basis size and collective-space cut-off,
we assumed an error of 15%. This is larger than the 10%
uncertainties related to the basis size only, which were assumed
in Ref. [15].
Systematic errors related to the form and parametrization of the
functional itself were not included in the error budget. Moreover,
similarly to our previous works [14,15], transition
![]() K
K
![]()
![]() Ar was disregarded. We recall that for
this transition, the calculated value of the ISB correction is
unacceptably large because of a strong mixing of Nilsson levels
originating from the
Ar was disregarded. We recall that for
this transition, the calculated value of the ISB correction is
unacceptably large because of a strong mixing of Nilsson levels
originating from the ![]() and
and ![]() sub-shells. The problem
can be partially cured by performing configuration-interaction
calculations, see Ref. [18] and discussion in
Sect. 4.2.
sub-shells. The problem
can be partially cured by performing configuration-interaction
calculations, see Ref. [18] and discussion in
Sect. 4.2.
| Parent |
|
|
|
||||
| nucleus | (s) | (%) |
(s)
|
(%) |
|||
| 3042(4) | 0.579(87) | 3064.5(52) | 0.37(15) | 3.5 | |||
| 3042.3(27) | 0.303(30) | 3072.3(33) | 0.36(6) | 0.0 | |||
| 3052(7) | 0.270(41) | 3081.4(72) | 0.62(23) | 1.4 | |||
| 3053(8) | 0.87(13) | 3063.6(91) | 0.63(27) | 1.3 | |||
| 3036.9(9) | 0.329(49) | 3071.8(20) | 0.37(4) | 0.8 | |||
| 3049.4(12) | 0.75(11) | 3067.6(38) | 0.65(5) | 10.9 | |||
| 3047.6(14) | 0.77(27) | 3069.2(85) | 0.72(6) | 3.1 | |||
| 3049.5(9) | 0.563(84) | 3075.1(32) | 0.71(6) | 1.3 | |||
| 3048.4(12) | 0.476(71) | 3076.5(32) | 0.67(7) | 2.4 | |||
| 3050.8(
|
0.586(88) | 3075.6(36) | 0.75(8) | 1.3 | |||
| 3074.1(15) | 0.78(12) | 3093.1(48) | 1.51(9) | 43.2 | |||
| 3085(8) | 1.63(24) | 3078(12) | 1.86(27) | 0.3 | |||
|
|
3073.7(11) | 69.5 | |||||
|
|
0.97396(25) |
|
6.3 | ||||
| 0.99937(65) |
| Parent |
|
Parent |
|
||||
| nucleus | nucleus | ||||||
| (%) | (%) | ||||||
| 1.37(21) | 1.22(18) | ||||||
| 0.427(64) | 0.335(50) | ||||||
| 1.24(19) | 0.98(15) |
To conform with the analyzes of Hardy and Towner (HT) and Particle Data
Group, the average value
![]() s was
calculated using the Gaussian-distribution-weighted formula. This
leads to the value of
s was
calculated using the Gaussian-distribution-weighted formula. This
leads to the value of
![]() , which is in a very good agreement
both with the Hardy and Towner result [29],
, which is in a very good agreement
both with the Hardy and Towner result [29],
![]() , and central value obtained from
the neutron decay
, and central value obtained from
the neutron decay
![]() [30]. By combining the value of
[30]. By combining the value of
![]() calculated here with those of
calculated here with those of
![]() and
and
![]() of the 2014 Particle Data Group [3],
one obtains
of the 2014 Particle Data Group [3],
one obtains
The last two columns of Table 1 show results of the
confidence-level (CL) test, as proposed in Ref. [28]. The CL
test is based on the assumption that the CVC hypothesis is valid up
to at least ![]() %, which implies that a set of
structure-dependent corrections should produce statistically
consistent set of
%, which implies that a set of
structure-dependent corrections should produce statistically
consistent set of ![]() -values. Assuming the validity of the
calculated corrections
-values. Assuming the validity of the
calculated corrections
![]() [31], the
empirical ISB corrections can be defined as:
[31], the
empirical ISB corrections can be defined as:
The empirical ISB corrections deduced in this way are tabulated in
Table 1. The table also lists individual
contributions to the ![]() budget, whereas the total
budget, whereas the total ![]() per
degree of freedom (
per
degree of freedom (
![]() for
for ![]() ) is
) is
![]() . This number is
considerably smaller than the number quoted in our previous
work [15], but much bigger than those obtained within (i) perturbative-model
reported in Ref. [28] (1.5), (ii)
shell model with the Woods-Saxon radial wave
functions (0.4) [27], (iii) shell model with
Hartree-Fock radial wave functions (2.0)
[32,33], (iv) Skyrme-Hartree-Fock with RPA (2.1)
[34], and relativistic Hartree-Fock plus RPA model
(1.7) [35]. It is
worth stressing that, as before, our value of
. This number is
considerably smaller than the number quoted in our previous
work [15], but much bigger than those obtained within (i) perturbative-model
reported in Ref. [28] (1.5), (ii)
shell model with the Woods-Saxon radial wave
functions (0.4) [27], (iii) shell model with
Hartree-Fock radial wave functions (2.0)
[32,33], (iv) Skyrme-Hartree-Fock with RPA (2.1)
[34], and relativistic Hartree-Fock plus RPA model
(1.7) [35]. It is
worth stressing that, as before, our value of
![]() is
deteriorated by two transitions that strongly violate the CVC
hypothesis,
is
deteriorated by two transitions that strongly violate the CVC
hypothesis, ![]() Ga
Ga
![]() As and
As and
![]() Cl
Cl
![]() S. These transitions give the 62% and
15% contributions to the total error budget, respectively. Without them,
we would have obtained
S. These transitions give the 62% and
15% contributions to the total error budget, respectively. Without them,
we would have obtained
![]() .
.
Jacek Dobaczewski 2016-03-05