


Next: Tetrahedral Magic Numbers in
Up: Interplay Between Tetrahedral and
Previous: Octahedral Symmetry
Before proceeding, let us recall in passing an important mathematical relation
between the tetrahedral and octahedral symmetries as represented in terms of
spherical harmonics. This relation originates from the fact that the tetrahedral
symmetry point-group is a sub-group of the octahedral one. Indeed, a surface
with the octahedral symmetry is invariant under 48 symmetry elements, among
others the inversion. It turns out that the ensemble of the 24 symmetry
operations of the octahedral group that do not contain the inversion operation
coincides with the 24 symmetry elements of the tetrahedral group. Consequently,
all the surfaces invariant under the octahedral symmetry group are at the same
time invariant under the tetrahedral symmetry group. One may show that the
Figure:
Illustration of the interplay between the tetrahedral and
octahedral geometrical symmetries. The figure shows a pure
tetrahedral symmetry surface corresponding to the deformation
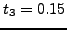 (left), compared to the pure octahedral symmetry surface
with
(left), compared to the pure octahedral symmetry surface
with 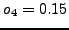 (middle), compared to the surface obtained by
superposition of the two (right). One can demonstrate that the
latter surface is still tetrahedrally symmetric.
This is also why combining the two symmetries simultaneously may
strengthen the final tetrahedral symmetry effect.
(middle), compared to the surface obtained by
superposition of the two (right). One can demonstrate that the
latter surface is still tetrahedrally symmetric.
This is also why combining the two symmetries simultaneously may
strengthen the final tetrahedral symmetry effect.
 |
mathematical expressions given in (12)-(17) are compatible in
this sense, and thus an arbitrary combination of nuclear shapes defined by
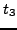 ,
, 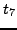 , and
, and 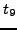 on the one hand, and
on the one hand, and 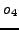 ,
, 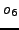 , and
, and 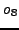 on the
other hand, preserves the tetrahedral symmetry while setting
on the
other hand, preserves the tetrahedral symmetry while setting 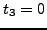 ,
,
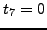 and
and 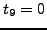 we obtain surfaces of pure octahedral symmetry.
we obtain surfaces of pure octahedral symmetry.
The above inter-relations are illustrated in Fig. 1 using typical
sizes of the tetrahedral and octahedral deformations as predicted by
microscopic calculations.



Next: Tetrahedral Magic Numbers in
Up: Interplay Between Tetrahedral and
Previous: Octahedral Symmetry
Jacek Dobaczewski
2006-10-30

