

Next: Determination of effective s.p.
Up: Theoretical framework
Previous: Definition of observables
Additivity of effective s.p. observables
For
each 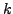 -configuration
defined by occupying a given set of
s.p. orbitals and represented by a product state
-configuration
defined by occupying a given set of
s.p. orbitals and represented by a product state 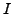 ,
we determine the average value
,
we determine the average value
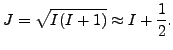 of a s.p. operator
of a s.p. operator
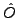 . We may now designate one of these configurations as
a reference, or a core configuration, and determine the relative
change
. We may now designate one of these configurations as
a reference, or a core configuration, and determine the relative
change
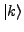 of the physical observable in
the
of the physical observable in
the 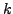 -th configuration with respect to that in the core
configuration. The additivity principle stipulates that all these
differences can be expressed as sums of individual effective
contributions
-th configuration with respect to that in the core
configuration. The additivity principle stipulates that all these
differences can be expressed as sums of individual effective
contributions
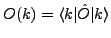 coming from s.p. states
(enumerated by index
coming from s.p. states
(enumerated by index 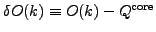 ),
i.e.,
),
i.e.,
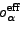 |
(19) |
Coefficients 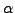 in Eq. (19)
define the s.p. content
of the configuration
in Eq. (19)
define the s.p. content
of the configuration 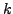 with respect to the core configuration. Namely,
with respect to the core configuration. Namely,
- (i)
-
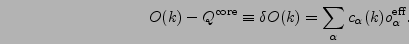 if the state
if the state 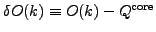 is not occupied in either of these
two configurations, or is occupied in both of them,
is not occupied in either of these
two configurations, or is occupied in both of them,
- (ii)
-
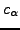 if
if 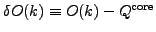 has a particle character
(it is occupied in the
has a particle character
(it is occupied in the 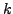 -th configuration and is not occupied
in the core configuration),
-th configuration and is not occupied
in the core configuration),
- (iii)
-
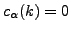 if the state
if the state 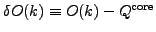 has a hole
character (it is not occupied in the
has a hole
character (it is not occupied in the 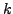 -th
configuration and is occupied in the core configuration).
-th
configuration and is occupied in the core configuration).
In this way, one can label the 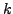 -th configuration with the set of
coefficients
-th configuration with the set of
coefficients
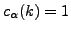 , where
, where
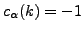 denotes the size of s.p. space considered. The
values of
denotes the size of s.p. space considered. The
values of
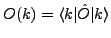 can be calculated by proceeding step by
step from the core configuration to the configurations differing by
one particle or one hole, then to the configurations differing by two
particles, two holes, or a particle and a hole, and so forth, until the
data set is generated which is statistically large enough to provide
appreciable precision for
can be calculated by proceeding step by
step from the core configuration to the configurations differing by
one particle or one hole, then to the configurations differing by two
particles, two holes, or a particle and a hole, and so forth, until the
data set is generated which is statistically large enough to provide
appreciable precision for
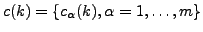 . Had the additivity principle been
obeyed exactly, calculations limited to one-particle and one-hole configurations
would have sufficed. Since our goal is not only to determine values
of
. Had the additivity principle been
obeyed exactly, calculations limited to one-particle and one-hole configurations
would have sufficed. Since our goal is not only to determine values
of
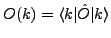 but actually prove that the additivity principle
holds up to a given accuracy, we have to consider a large set of
configurations and determine the best values of
but actually prove that the additivity principle
holds up to a given accuracy, we have to consider a large set of
configurations and determine the best values of
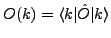 together with their error bars.
together with their error bars.
In what follows, we consider relative changes in the average quadrupole
moments
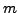 and
and
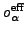 , transition
quadrupole moments
, transition
quadrupole moments 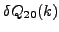 , and total angular momenta
, and total angular momenta 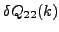 (see
Sec. 2.1), which are related to the
effective one-body expectation values via the additivity principle.
(see
Sec. 2.1), which are related to the
effective one-body expectation values via the additivity principle.
The addition of particle or hole in a specific single-particle
orbital 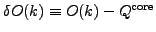 gives rise to a polarization of the system, so the effective
s.p. values,
gives rise to a polarization of the system, so the effective
s.p. values,
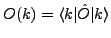 , depend not
only on the bare s.p. expectation values,
, depend not
only on the bare s.p. expectation values,
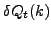 , but also
contain polarization contributions. For example, the effective
s.p. charge quadrupole moment
, but also
contain polarization contributions. For example, the effective
s.p. charge quadrupole moment
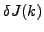 can be represented as the sums of bare s.p. charge
quadrupole moments
can be represented as the sums of bare s.p. charge
quadrupole moments
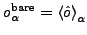 and polarization contributions
and polarization contributions
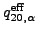 :
:
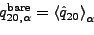 |
(20) |
Therefore, for neutron orbitals, which have vanishing bare
charge quadrupole moments,
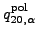 ,
the effective charge quadrupole moments are solely given
by polarization terms:
,
the effective charge quadrupole moments are solely given
by polarization terms:
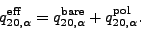 |
(21) |


Next: Determination of effective s.p.
Up: Theoretical framework
Previous: Definition of observables
Jacek Dobaczewski
2007-08-08
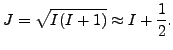 of a s.p. operator
of a s.p. operator
![]() -configuration
defined by occupying a given set of
s.p. orbitals and represented by a product state
-configuration
defined by occupying a given set of
s.p. orbitals and represented by a product state ![]() ,
we determine the average value
,
we determine the average value
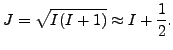 of a s.p. operator
of a s.p. operator
![]() . We may now designate one of these configurations as
a reference, or a core configuration, and determine the relative
change
. We may now designate one of these configurations as
a reference, or a core configuration, and determine the relative
change
![]() of the physical observable in
the
of the physical observable in
the ![]() -th configuration with respect to that in the core
configuration. The additivity principle stipulates that all these
differences can be expressed as sums of individual effective
contributions
-th configuration with respect to that in the core
configuration. The additivity principle stipulates that all these
differences can be expressed as sums of individual effective
contributions
![]() coming from s.p. states
(enumerated by index
coming from s.p. states
(enumerated by index ![]() ),
i.e.,
),
i.e.,
![]() and
and
![]() , transition
quadrupole moments
, transition
quadrupole moments ![]() , and total angular momenta
, and total angular momenta ![]() (see
Sec. 2.1), which are related to the
effective one-body expectation values via the additivity principle.
(see
Sec. 2.1), which are related to the
effective one-body expectation values via the additivity principle.
![]() gives rise to a polarization of the system, so the effective
s.p. values,
gives rise to a polarization of the system, so the effective
s.p. values,
![]() , depend not
only on the bare s.p. expectation values,
, depend not
only on the bare s.p. expectation values,
![]() , but also
contain polarization contributions. For example, the effective
s.p. charge quadrupole moment
, but also
contain polarization contributions. For example, the effective
s.p. charge quadrupole moment
![]() can be represented as the sums of bare s.p. charge
quadrupole moments
can be represented as the sums of bare s.p. charge
quadrupole moments
![]() and polarization contributions
and polarization contributions
![]() :
: